Интегрирование тригонометрических и иррациональных функций
Интегрирование тригонометрических функций
Интегрирование иррациональных функций
Интегрирование
тригонометрических функций
Универсальная тригонометрическая подстановка
Функцию с переменными sin x и cos x, над которыми выполняются рациональные действия принято обозначать
R(sin x;cos x)
Вычисление неопределенных интегралов типа:
Знак рациональной функции
R(sin x;cos x) dx
сводится к вычислению интегралов от рациональной функции с помощью подстановки, которую называют универсальной:
|
|
|
|
|
2tg |
x2 |
|
x |
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x |
|
1 tg |
|
|
|
|
|
2t |
|
|
|
|
|
|
|||||
|
|
2t 2 2 |
|
|
|
|
|
|
|
2dt |
||||||||||
tg t |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
1 dt |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 2t |
|
|
|
|
|
|
|
|
|
|
|
|
sinxx 2arct2g; t cosdx 2 |
2 22; |
dx |
|
2 |
||||||||||||
|
|
|
|
sincosxx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
22xx |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
11 tt |
t |
|
|
|
|||||||||||
|
|
|
|
1 1t1 tgtg |
|
|
|
|
|
1 t |
|
|
|
|
1 t |
|
||||
|
|
|
|
22 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Интегрирование
тригонометрических функций
На практике применяют и другие, более простые подстановки, в зависимости от вида подынтегральной функции R(sin x;cos x)
Если функция нечетна относительно sin x, то есть:
R( sin x;cos x) R(sin x;cos x)
то применяется подстановка cos x = t.
Если функция нечетна относительно cos x, то есть:
R(sin x; cos x) R(sin x;cos x)
то применяется подстановка sin x = t.
Если функция четна относительно cos x и sin x, то есть:
R( sin x; cos x) R(sin x;cos x) |
тогда: |
|||||||||
tgx t |
2 |
|
t 2 |
|
2 |
|
|
1 |
|
dt |
sin |
x 1 t 2 ; cos |
|
x 1 |
t 2 |
; dx 1 t 2 |
|||||
|
|
|||||||||
Интегрирование |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
тригонометрических функций |
|
2t |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
dx |
|
|
|
|
tg |
x |
t; |
|
|
|
|
|
sin x |
|
; |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 t |
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 sin x cos x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
cos x 1 t |
2 |
|
; |
dx |
|
2dt |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 t 2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
2dt |
|
|
|
|
|
|
|
|
|
1 t 2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2dt |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
1 t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2t |
1 t 2 |
|
1 t 2 2t 1 t 2 |
|
|
|
2 |
|
||||||||||||||||||||
|
|
1 |
|
|
|
|
1 t 2 |
|
|
|
|
|
|
1 t 2 |
1 t |
|
|
|
||||||||||||
|
|
1 t 2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
t 1 |
ln |
t 1 |
C |
ln |
tg |
2 1 |
|
C |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Интегрирование
тригонометрическихm n функций
Интегралы типа: sin x cos x dx
Используются следующие подстановки:
Если n – целое положительное нечетное число: sin x = t
Если m – целое положительное нечетное число: cos x = t
В этих двух случаях можно также произвести «отщепление» одной из нечетных степеней с последующим внесением под знак дифференциала.
Если m и n - целые неотрицательные четные числа, то применяются формулы понижения степени:
sin2 x |
1 |
(1 cos 2x); |
cos2 x |
1 |
(1 cos 2x) |
|
2 |
|
|
2 |
|
Если m + n - отрицательное четное целое число, то применяется подстановка: tg x = t
Интегрирование
тригонометрических функций
sin7 x cos3 xdx sin7 x cos2 x cos xdx
|
sin7 |
x(1 sin2 x)d(sin x) (sin7 x |
sin9 |
x)d |
(sin x) |
||||||||||||||||||
|
|||||||||||||||||||||||
|
|
|
|
|
8 |
10 |
|
|
|
|
|
|
|
|
|
|
|
1 sin2 x |
|
|
|||
|
sin |
|
x sin x C |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
8 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
sin |
4 |
|
|
|
1 |
(1 |
|
|
|
2 |
dx |
|
|
|
|
||||||||
|
x dx |
2 |
cos2x) |
|
|
|
|
||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|||
1 |
2cos2x cos2 2x dx |
|
|
|
dx |
cos2xdx |
|||||||||||||||||
4 |
4 |
|
|
|
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 |
1 cos 4x dx |
1 |
x |
1 |
sin2x 1 x |
1 |
sin2x C |
||||||||||||||||
8 |
4 |
4 |
32 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|||||||||
Интегрирование
тригонометрических функций
Интегралы типа:
sinax cosbx dx; |
cosax cosbx dx; |
sinax sin bx dx |
Вычисляются с помощью формул тригонометрии:
sin x cos x 0.5(sin( ) sin( )); cos x cos x 0.5(cos( ) cos( )); sin x sin x 0.5(cos( ) cos( ))
sin8x cos2xdx |
0.5 (sin10x sin6x) dx |
||||||||
0.5( |
|
1 |
cos10x |
1 cos6x) C |
|
|
|
||
10 |
|
|
|
||||||
|
|
6 |
1 |
|
|
1 |
|
||
|
|
|
|
|
cos10x |
|
cos6x C |
||
|
|
|
|
|
12 |
||||
|
|
|
|
20 |
|
|
|||
Интегрирование иррациональных
Рассмотримфункцийинтегралы от некоторых иррациональных функций, которые с помощью подстановок приводятся к интегралам от рациональных функций новой переменной.
|
|
|
|
|
|
|
|
|
|
|
Интегралы вида: R(x, m x , n |
x )dx |
|
|
|
||||||
сводятся к интегралу от рациональной функции подстановкой |
||||||||||
x t N где N – наименьшее общее кратное (НОК) значений m и n. |
||||||||||
|
|
|
|
|
|
|
||||
|
ax b |
|
|
ax b |
|
|||||
Интегралы вида: R(x, m |
|
, n |
|
|
)dx |
|||||
|
cx d |
|
|
cx d |
|
|
||||
где a, b, c, d – постоянные, приводится к интегралу от рациональной функции с помощью подстановки:
ax b |
t N |
где N – наименьшее общее кратное m и n. |
cx d |
|
|
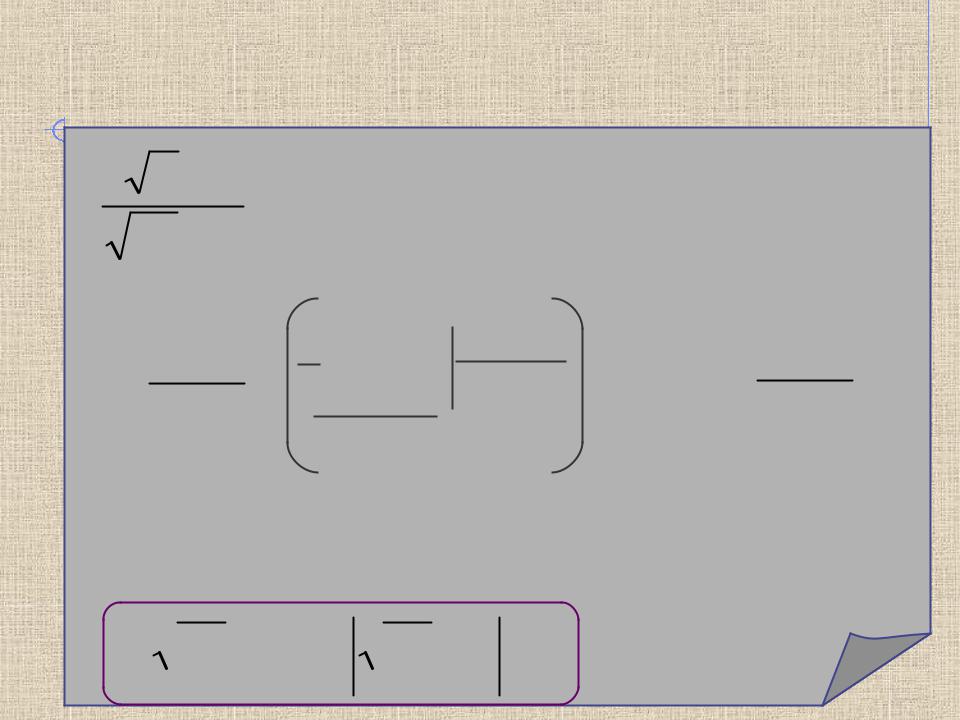
Интегрирование иррациональных |
|
||||||||||||||||||||||||
функций |
НОК(2; 4) 4 |
|
t 2 4t3dt |
|
|
|
|
|
|||||||||||||||||
|
xdx |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
4 x3 4 |
x t |
|
|
|
|
|
|
|
t3 |
4 |
|
|
|
|
|||||||||||
|
|
|
|
3 |
dt |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
dx 4t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
t |
5 |
dt |
|
t |
5 |
|
|
|
|
t |
3 |
4 |
|
|
|
|
4t |
2 |
|
||||
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
4 |
|
|
|
t |
5 |
4t |
2 |
t |
2 |
|
|
|
|
|
|
|
|||||||||
t |
3 |
|
4 |
|
|
|
|
|
|
|
4 t |
|
t |
3 |
4 |
dt |
|||||||||
|
|
|
|
|
|
4t 2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
dt |
16 d(t3 4) |
|
4 |
16 |
|
t3 4 |
|
C |
|
|
|
||||||||
4 t |
|
3 t3 4 |
3 t3 |
3 |
ln |
|
||||
|
|
|
|
|
|
|
34 4
x3 163 ln 4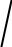
x3 4 C
Интегрирование иррациональных
функций |
|
|
|
|
|
|
R(x, ax |
2 |
bx c) |
||
Иррациональные функции вида: |
|
|
|
||
|
|
|
|
||
выделением полного квадрата сводятся к 3-м видам функций, для каждой, из которой применяется свой вид подстановки:
|
|
|
|
|
u a sint |
|||
1) R(u, |
|
a2 u2 ) |
подстановка: |
|||||
|
|
|
|
u a tg t |
||||
2) R(u, |
a2 u2 ) |
подстановка: |
||||||
|
|
|
|
u |
a |
|
||
3) R(u, |
u2 a2 ) |
подстановка: |
||||||
cost |
||||||||
|
|
|
|
|
|
|||