
Тема 8 вибрация и методы ее устранения
ОСНОВНЫЕ СВЕДЕНИЯ
Надежность работы оборудования (турбоустановки, насосы) на электростанциях в значительной мере определяется его вибрационным состоянием. Уровень вибрации подшипников турбины, генератора и возбудителя является основным показателем качества ремонта машины, уравновешенности роторов и муфт, правильности режима эксплуатации.
В общем случае вибрация является результатом действия возмущающих механических колебаний машин и механизмов.
Основным источником возмущения колебаний турбоустановки является его валопровод. Колебания валопровода передаются через масляную пленку подшипников на опоры, статоры, фундамент и грунт, а через грунт – на окружающие конструкции. Возможна и обратная передача колебаний от соседних агрегатов. Валопровод турбоагрегата – это совокупность соединенных между собой роторов, в последовательно расположенных цилиндрах, генератора и возбудителя.
По упругим свойствам роторы условно можно разделить на жесткие и гибкие. В общем случае ротор, рабочая частота вращения которого выше критической частоты вращения, называется гибким ротором; в противоположном случае ротор называется жестким.Жесткий роторне меняет своей конфигурации под действием приложенных к нему неуравновешенных сил, рабочая скорость его вращения лежит ниже половины от первой критической скорости.Гибкий роторпри тех же условиях испытывает заметный прогиб. Большинство роторов современных турбоагрегатов являются гибкими.
Частота вращения вала, при которой наблюдается наибольший его прогиб, называется критической частотой вращения.
Наиболее частыми причинами вибрации турбоагрегата при пуске после капитального ремонта являются: неуравновешенность вращающихся частей; расцентровка валов; неправильная работа соединительных муфт; неправильная установка подшипников и уплотнений.
Неуравновешенность вращающихся частей турбоагрегата возникает из-за перераспределения масс по окружности ротора и смещения главной центральной оси инерции ротора относительно оси его вращения.
Неуравновешенность ротора вызывает при его вращении появление возмущающей силы, стремящейся нарушить состояние подвижного равновесия. Величина возмущающей силы, вызываемой небалансом, равна центробежной силе неуравновешенной массы и может быть определена по формуле:
 ,
(6.1)
,
(6.1)
где Q– вес неуравновешенной массы (небаланс),
кг;g
– ускорение силы тяжести, равное
9,81 м/сек2;![]() – угловая скорость вращения, определяемая
по формуле (6);R
– радиус приложения неуравновешенной
массы, м
– угловая скорость вращения, определяемая
по формуле (6);R
– радиус приложения неуравновешенной
массы, м
 ,
(6.2)
,
(6.2)
где n– число оборотов в минуту.
Неуравновешенность подразделяется на статическую и динамическую. Ротор, неуравновешенные массы которого приводятся к массе, создающей одиночную центробежную силу при его вращении, является статически неуравновешенным. Ротор неуравновешенные массы которого при вращении дают две равные, противоположно направленные и лежащие в одной плоскости центробежные силы (пару сил), называетсядинамически неуравновешенным.
Одним из основных средств уменьшения вибрации является балансировка вращающихся тел (наряду с центровкой). Балансировка роторов – это технологический процесс совмещения главной центральной оси инерции с осью вращения ротора. Балансировка производится путем компенсации дисбалансов установкой корректирующих масс(балансировочных грузов) в доступныеплоскости коррекции(балансировочные плоскости), перпендикулярные к оси вращения и расположенные вдоль этой оси. В зависимости от вида неуравновешенности балансировка подразделяется на статическую и динамическую. Пристатической балансировкиротор, либо отдельные его части (диски, полумуфты и др.), устанавливаются на опоры (призмы). Центр масс при этом изначально оказывается не в нижней точке, и исходя из условий устойчивого равновесия, ротор перекатывается таким образом, что центр масс занимает низшее положение. Статическая балансировка производится в общем случае без вращения, т.е. в статике, поэтому она и носит название статической.
При динамической балансировки(в дальнейшем просто балансировки) жесткого ротора определяются места расположения и величины грузов, в двух плоскостях поперечных его оси, которые вызовут в роторе добавочные центробежные силы, равные по величине и противоположные по направлению центробежным силам, создающим неуравновешенность ротора.
Балансировка жесткого ротора производится на любой одной частоте вращения. Будучи уравновешенным на одной частоте вращения ротор останется уравновешенным на любой другой частоте вращения во всем рабочем диапазоне частот вращения. Ниже приводятся общий подход и два метода балансировки жестких роторов.
БАЛАНСИРОВКА ЖЕСТКИХ РОТОРОВ
Первым балансируется тот конец ротора, амплитуда колебаний которого была наибольшей. Допустим, что первым балансируется ротор со стороны А (рис. 6.2). После определения величины первоначальной вибрации выбирается пробный груз. Пробный грузР(г) берется равным 0,6 ÷ 0,7 величины небалансаН (табл. 6.1) и с учетом веса ротораG (т):
![]() (6.3)
(6.3)
Рис. 6.2 Схема для
пересчета грузов после балансировки
второго конца ротора
a,
m,
n,
b
– длины от подшипников до ротора, мм;
r,
s
– радиусы крепления уравновешивающих
грузов, мм; r1
– радиус крепления пробного груза, мм;
К – уравновешивающий груз (г) для конца
А; W
– уравновешивающий груз (г) для конца
Б. Укрепив
пробный грузР производят
серию пусков и замеров величин колебаний.
Для снижения амплитуды колебаний на
сторонеАустанавливают
уравновешивающий грузК.
Укрепив
пробный грузР производят
серию пусков и замеров величин колебаний.
Для снижения амплитуды колебаний на
сторонеАустанавливают
уравновешивающий грузК.
После этого аналогичным способом балансируется ротор со стороны Б. Определяется пробный грузР и уравновешивающий –W. Крепление грузаW, найденного для второго конца ротораБ , вызовет небаланс на первом концеА. Для того чтобы балансировка стороны ротораА не была нарушена, необходимо грузW разложить на два грузаX иYсоответственно уравнениям:
![]() (6.4)
(6.4)
![]() (6.5)
(6.5)
При этом груз Y необходимо укрепить диаметрально противоположно грузуW на противоположном конце ротора (т.е. со стороныА), а грузX установить вместо грузаW. ГрузыX иY вместе с грузомК должны привести ротор в динамическое равновесие.
Таблица 6.1
Примерная величина небаланса Н вг на 1т веса ротора
при 3000 об/мин
|
Радиус крепления груза, r1, мм |
Амплитуда вибрации , мм | |||||||
|
0,05 |
0,10 |
0,15 |
0,20 |
0,25 |
0,30 |
0,35 |
0,40 | |
|
100 |
75 |
150 |
225 |
300 |
375 |
– |
– |
– |
|
200 |
37 |
75 |
112 |
150 |
187 |
225 |
262 |
300 |
|
300 |
25 |
50 |
75 |
100 |
125 |
150 |
175 |
200 |
|
350 |
22 |
43 |
65 |
87 |
108 |
130 |
152 |
174 |
|
400 |
19 |
38 |
56 |
75 |
94 |
112 |
131 |
150 |
|
450 |
17 |
33 |
50 |
67 |
84 |
100 |
117 |
135 |
|
500 |
15 |
30 |
45 |
60 |
75 |
90 |
105 |
120 |
|
550 |
13 |
27 |
40 |
54 |
67 |
80 |
94 |
108 |
|
600 |
12 |
25 |
37 |
50 |
62 |
75 |
87 |
100 |
Балансировка методом 3-х пусков
Согласно замерам первоначальной вибрации, которые составили 0, первой балансируется сторона А. Описываем окружность радиусомR0равным0. Принимается, что 0,01 мм вибрации соответствует 1 мм.
Пробный груз Р, подсчитанный по формуле 6.3 и выбранный согласно табл.6.1, помещается в любом месте по окружности диска (т. 1 на рис. 6.3). Машина пускается в ход и при нормальном числе оборотов замеряется вибрация1. Тот же груз помещают в другой точке 2, расположенной под углом 90º к точке 1. Фиксируется вибрация при втором пуске2.
Далее определяется величина и место уравновешивающего груза (К). Из точек 1 и 2 описываются окружности радиусамиR1=1, R2=2. Точку пересечения этих окружностей (т.А) соединяем с центромОи продолжаем до пересечения с окружностью, описанной из точкиО (т.Б), которая и определяет место установки уравновешивающего груза. Измеряем длину отрезкаОА. Длина отрезкаОБявляется радиусом будет являться радиусомs крепления уравновешивающего груза на сторонеА. Величина уравновешивающего груза определяется:
 (6.6)
(6.6)
П осле
балансировки одной стороны ротораАбалансируется другая сторонаБ
(грузW).
Окончательно устанавливаются следующие
грузы (см. рис. 6.2 и формулы 6.4 и 6.5): на
первом конце ротораА
грузыК и
Y,
диаметрально противоположные грузуW
; на втором конце ротораБ
– грузX
в точке расположения грузаW.
Величина уравновешивающего грузаW
определяется аналогично (6.6).
Здесь длина отрезкаОБ
будет являться радиусомrкрепления уравновешивающего груза на
сторонеБ.
осле
балансировки одной стороны ротораАбалансируется другая сторонаБ
(грузW).
Окончательно устанавливаются следующие
грузы (см. рис. 6.2 и формулы 6.4 и 6.5): на
первом конце ротораА
грузыК и
Y,
диаметрально противоположные грузуW
; на втором конце ротораБ
– грузX
в точке расположения грузаW.
Величина уравновешивающего грузаW
определяется аналогично (6.6).
Здесь длина отрезкаОБ
будет являться радиусомrкрепления уравновешивающего груза на
сторонеБ.
Рис. 6.3 Графическое
определение величины небаланса при
балансировке методом трех пусков
Балансировка методом 3-х последовательных креплений
пробного груза
Согласно замерам первоначальной вибрации, которые составили 0, первой балансируется сторона А. Пробный грузР, подсчитанный по формуле 6.3 и выбранный согласно табл.6.1, помещается поочередно в точкаха,б ис, расположенных друг относительно друга под углом в 120º. Производят пуски турбины и замеряют амплитуды вибрации, соответственноа,б, с.

Рис. 6.4 Построение
равностороннего треугольника с
использованием специальной линейки
Далее графическим способом определяются направления и величины небаланса. Из центра S1 (рис. 6.5) строят три окружности с радиусамиRа=а, Rб=б,Rс=с. На полученных трех окружностях путем подбора строят равносторонний треугольникабс, вершины которого расположены друг относительно друга под углом в 120º. Построение равностороннего треугольника значительно облегчается использованием специальной миллиметровой линейки (рис. 6.4), изготовленной на листе прозрачной бумаги.
В построенном треугольнике (рис. 6.5) проводят биссектрисы углов, которые пересекутся в точке О. Соединив точкуО с точкойS1, который даст направление и величину небаланса.
Местоположение вектора небаланса на роторе определяют относительно основных точек а,б,с. Центр окружности будет в точкеО.
Величину дуги сS ибS в соответствующем масштабе переносят на ротор, на котором в точкеSи укрепляют уравновешивающий грузК.

Рис. 6.5 Графическое
определение величины и направления
небаланса при
балансировке
обходом трех грузов
Величина уравновешивающего груза К (кг) определяется по формуле:
 , (6.7)
, (6.7)
где Р– пробный груз, кг;RР– радиус окружности, проведенной через вершины треугольникаабс, мм; S1О – вектор небаланса, мм.
Длина отрезка OS =RР, в данном случае, будет являться радиусомs крепления уравновешивающего груза на сторонеА.
Далее определяется подобным же образом груз W для второго конца ротораБ. Так как крепление грузаW, найденного для второго конца ротора, вызовет небаланс на первом конце ротора, то в этом случае подобно предыдущему методу балансировки определяются балансирующие грузыX иY (см. формулы 6.4 и 6.5), которые необходимо укрепить вместо грузаW. Длина отрезкаOS =RР, здесь, будет являться радиусомrкрепления уравновешивающего груза на сторонеБ.
БАЛАНСИРОВКА ГИБКИХ РОТОРОВ
Колебания гибких роторов качественно отличны от колебаний жестких роторов. Это проявляется в изменении формы упругой линии вала при вращении на разных скоростях, в появлении упругого прогиба ротора под влиянием неуравновешенности и балансировочных грузов, в различном эффекте воздействия одинаковых пробных грузов (установленных в одних и тех же местах ротора) в зависимости от характера и распределения неуравновешенности вдоль бочки ротора и в существенном влиянии податливости и массы опор.
В основе метода балансировки гибких роторов лежит учет действительной формы упругой линии прогиба ротора, а также свойства ортогональности собственных форм колебаний гибкого вала. Это позволяет уравновешивать гибкие роторы на любой рабочей скорости путем установки определенной комбинации грузов, влияя на определенные гармоники небаланса. Характер размещения пробных и уравновешивающих грузов должен соответствовать форме прогиба ротора, а грузы устанавливаются в плоскости небаланса.
Далее излагается методика уравновешивания для случая близости первой критической скорости вращения ротора к рабочему числу оборотов (3000 об/мин).
Первый пуск дал начальные значения вибраций опор A0иВ0 (мк). Углы векторов начальных вибраций соответственноA0иB0 . С учетом этого ориентировочное значение небалансаQН(г) вычисляется по формуле:
 ,
(6.8)
,
(6.8)
где kc – коэффициент чувствительности, (принятьkc = 100),мк/кг.
Пробный груз Р(г), устанавливаемый под угломР, принимается равным 60% небаланса, т.е:
![]()
![]() (6.9)
(6.9)
Пуск с двумя пробными грузами весом Р(г) показал вибрацииA01 иВ01 с угламиA01иB01. Графически на плоскости (рис. 6.7) строятся векторы-вибрацииA0,В0,A01 иВ01 под соответствующими углами. Далее графически на плоскости (рис. 6.7) определяются векторы-вибрации от пробных грузовA1иВ1 с угламиA1иB1 исходя из формул 6.10, 6.11 и правила вычитания векторов (рис. 6.6 а).
![]() (6.10)
(6.10)
![]() (6.11)
(6.11)


![]()
а)
б)
Рис. 6.6 Сложение
и вычитание векторов
Исходя из этих условий подсчитываются величины балансировочных грузов (г):
 (6.12)
(6.12)
 ,
(6.13)
,
(6.13)
где
![]() и
и![]() соответственно величины балансировочных
грузов, устанавливаемые в опореА
иВ.
Знак "–" в расчетах не учитывать.
соответственно величины балансировочных
грузов, устанавливаемые в опореА
иВ.
Знак "–" в расчетах не учитывать.
Углы установки балансировочных грузов находятся из:
![]() (6.14)
(6.14)
![]() (6.15)
(6.15)
Средняя величина уравновешивающего груза и угол его установки определяются как среднеарифметическое:
 (6.16)
(6.16)
 (6.17)
(6.17)
Уравновешивающие грузы будут смещены на некоторый угол от места установки пробных грузов. Вибрация при пуске с этими уравновешивающими грузами составилаA02 иВ02 с угламиA2 иB2.
Далее производится корректировка полученных результатов. С этой целью графическим путем находятся векторы-разности вибраций последних двух пусков, с соответствующими углами A2 иB2:
![]() (6.18)
(6.18)
![]() ,
(6.19)
,
(6.19)
а также вектор-разность грузов
![]() ,
с углом1:
,
с углом1:
![]() .
(6.20)
.
(6.20)
Затем делается подсчет корректирующих грузов на каждую сторону ротора:
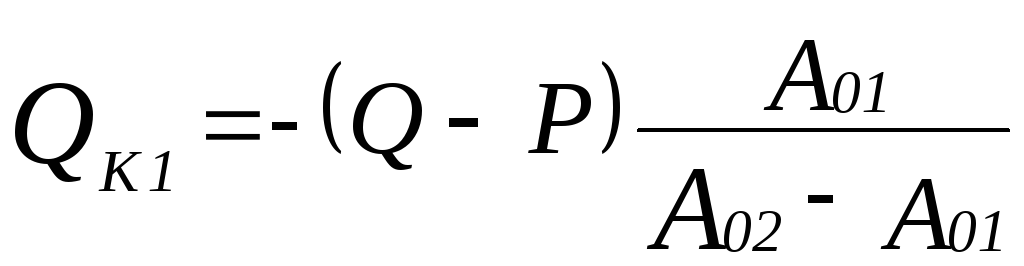 (6.21)
(6.21)
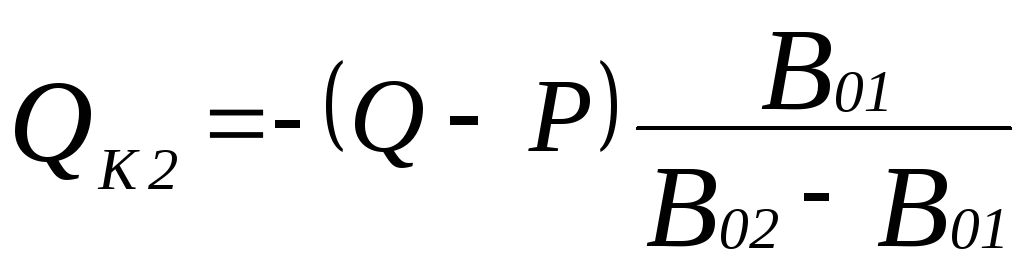 (6.22)
(6.22)
Знак "–" в расчетах не учитывать.
Углы установки корректирующих грузов находятся из:
![]() (6.23)
(6.23)
![]() (6.24)
(6.24)
Среднее значение корректирующих грузов и угол его установки определяются как среднеарифметическое:
![]() (6.25)
(6.25)
![]() (6.26)
(6.26)
В результате векторного сложения
окончательно получается значение
уравновешивающих грузов
![]() с
углом2:
с
углом2:
![]() (6.27)
(6.27)

Рис. 6.7 Графические
построения при уравновешивании гибкого
ротора
ЗАДАЧИ
1. В случае неуравновешенности ротора определить во сколько раз величина возмущающей силы больше величины небаланса вызвавшей ее. (Расчет сделать приn= 1500 и 3000 об/мин). Исходные данные для расчета указаны в таблице 7.23.
2. Определить величину уравновешивающих грузов К, X и Y (рис. 6.2) и место их расположения для ротора жесткого типа весом G т. Балансировку провести:
2а) методом 3-х пусков
2б) методом 3-х последовательных креплений пробного груза.
Исходные данные для расчета указаны в таблицах 7.24, 7.25.
3. Рабочая скорость вращения ротора
близка к первой критической. Определить
окончательный вес уравновешивающих
грузов![]() и угол их расположения2. Исходные данные для расчета указаны
в таблице 7.26.
и угол их расположения2. Исходные данные для расчета указаны
в таблице 7.26.
ВОПРОСЫ ДЛЯ ПРОВЕРКИ
Что такое вибрация?
Чем отличается жесткий ротор от гибкого?
Какая частота вращения ротора называется критической?
Что вызывает появление неуравновешенности вращающихся частей турбоагрегата и к чему она приводит?
Что такое называется статической и динамической неуравновешенностью ротора?
Что такое балансировка? Как она производится? Чем отличается статическая балансировка от динамической?
В чем проявляется особенность колебаний гибкого ротора?
