Критерий подобия двух числовых матриц

Пусть дана матрица 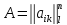 с числовыми элементами из поля K. Ее характеристическая матрица  является λ-матрицей ранга n и потому имеет n инвариантных многочленов

. (18)

Теорема

Для того чтобы две матрицы  и  были подобны  , необходимо и достаточно, чтобы они имели одни и те же инвариантные многочлены, или, что то же, одни и те же элементарные делители в поле K.

Доказательство

Условие необходимости. Действительно, если матрицы A и B подобны, то существует такая неособенная матрица T, что

. (19)

Отсюда

. (20)

Это равенство показывает, что характеристические матрицы  и 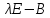  эквиваленты и потому имеют одни и те же инвариантные многочлены.

Условие достаточности. Пусть характеристические матрицы  и   имеют одни и те же инвариантные многочлены. Тогда эти λ-матрицы эквивалентны, и, следовательно, существуют две многочленные матрицы Р(λ) и Q(λ) такие, что

. (21)

Мы можем в тождестве (21) заменить λ-матрицы Р(λ) и Q(λ) постоянными матрицами P и Q:

,         (22)

причем в качестве P и Q можно взять соответственно левый и правый остатки от деления  и Q(λ) на , то есть можно положить:

.       (23)

Приравнивая в обеих частях равенства (22) коэффициенты при нулевой и при первой степенях λ, получим:

, (24)

то есть

,

где

.

Теорема доказана.

Жорданова матрица

Определение

Жордановой матрицей называется квадратная блочно-диагональная матрица над полем K, с блоками вида

(25)

при этом каждый блок 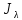называется жордановой клеткой с собственным значением λ (собственные значения в различных блоках могут совпадать).

Для произвольной квадратной матрицы А над алгебраически замкнутым полем К (например, полем комплексных чисел К=С) всегда существует квадратная невырожденная (т.е. обратимая, с отличным от нуля определителем) матрица С над К, такая, что

(26)

является жордановой матрицей. При этом матрица J называется жордановой формой (или жордановой нормальной формой) данной матрицы A. В этом случае также говорят, что жорданова матрица J в поле K подобна (или сопряжена) данной матрице A. И наоборот, в силу эквивалентного соотношения

(27)

матрица A подобна в поле K матрице J. Нетрудно показать, что введённое таким образом отношения подобия является отношением эквивалентности и разбивает множество всех квадратных матриц заданного порядка над данным полем на непересекающиеся классы эквивалентности.

Жорданова форма матрицы определена не однозначно, а с точностью до порядка жордановых клеток. Точнее, две жордановы матрицы подобны над полем K в том и только в том случае, когда они составлены из одних и тех же жордановых клеток и отличаются друг от друга лишь расположением этих клеток на главной диагонали.