
- •Глава 4. Плоскопараллельное движение нмс
- •4.1. Определение
- •4.2. Геометрический метод рассмотрения движения плоской фигуры в ее плоскости
- •4.3. Угловые скорость и ускорение плоской фигуры
- •4.4. Мгновенный центр вращения плоской фигуры
- •4.5. Теорема о скоростях точек плоской фигуры
- •4.6. Теорема о проекциях скоростей точек плоской фигуры
- •4.7. Мгновенный центр скоростей плоской фигуры
- •4.8. Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей
- •4.9. Способы определения положения мгновенного центра скоростей плоской фигуры
- •4.10. Теорема об ускорениях точек плоской фигуры
- •Примечание
- •4.11. Аналитический метод рассмотрения движения плоской фигуры
- •4.12. Алгоритм решения задач кинематики
- •С комментариями и примерами
- •Комментарии
- •Пример 2
- •Пример 3
- •Пример 4
- •4.13. Алгоритм решения задач кинематики
- •Пример 7
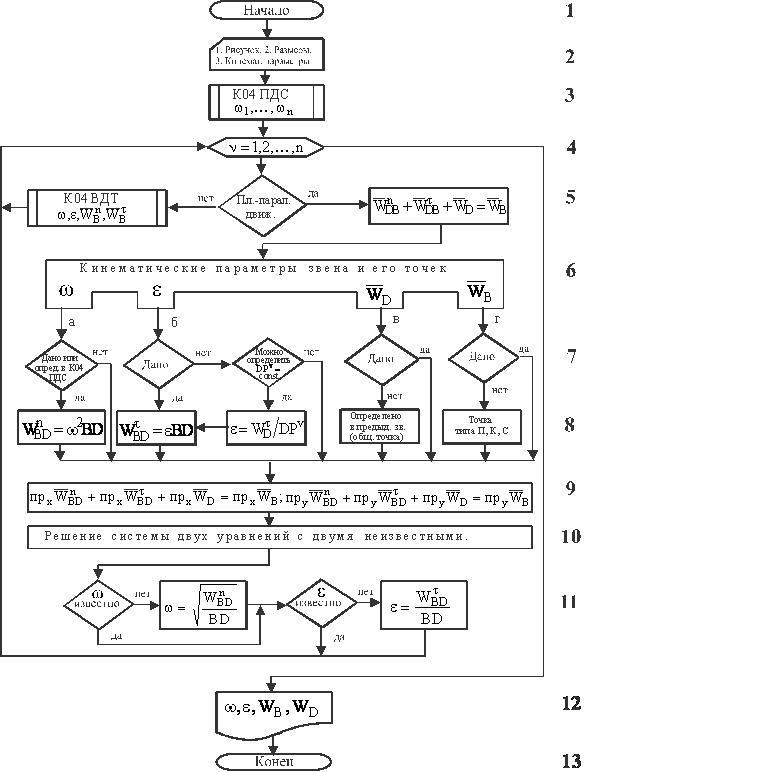
4.13. Алгоритм решения задач кинематики
плоскопараллельного движения НМС по определению
углового ускорения и ускорений точек
плоской фигуры – схема алгоритма К04 ПДУ
с комментариями и примерами
Комментарии
К.2 Изображается механизм в положении, соответствующем рассматриваемому моменту времени.
Разбивается механизм на n движущихся звеньев, которые нумеруются ( = 1,2,…,n) и выделяются общие точки звеньев, в которых происходит передача движения.
К.3 Определяются угловые скорости звеньев механизма с помощью схемы алгоритма К04 ПДС.
К.4 Начинается решение задачи со звена, какие-либо кинематические параметры движения которого заданы.
Решается задача с помощью теоремы об ускорениях точек плоской фигуры путем перехода от кинематических параметров одного звена к кинематическим параметрам другого через нахождение ускорений их общих точек. Для компактности в в уровнях 5-11 схемы алгоритма индекс опущен.
К.5 Записывается теорема об ускорениях точек плоской фигуры для двух точек одного звена, для которых неизвестных кинематических параметров не более двух.
Для некоторых звеньев теорему необходимо применять дважды: сначала для точек типа П, К, С (таблица 4), затем для точек, у которых неизвестны величина и направление ускорения, но их необходимо определить.
К.6-8
Выписываются
кинематические параметры звена и его
двух точек (,
,
![]() ).
).
Каждый из этих параметров либо задан, либо может быть определен, либо неизвестен.
К.7б Считается известным угловое ускорение для рассматриваемого звена после того, как оно определено в уровне 11.
К.7б-8б
Определяется
,
если расстояние от точки D
до точки Рv
– мгновенного центра скоростей звена
постоянно (DРv=const).
В этом случае, используя из К04 ПДС
формулу
![]() ,
можно определить
,
можно определить![]() .
.
К.6в-8в Выбирается в качестве полюса D чаще всего точка, ускорение которой либо задано, либо это точка, ускорение которой уже определено в предыдущем звене (общая точка двух звеньев).
К.8г Для точек типа П и С (таблица 4) известны направления и скорости, и ускорения.
Для
точек типа К (таблица 4), для которых (![]() ),
известны направления составляющих и
величина одной из составляющих
),
известны направления составляющих и
величина одной из составляющих![]() (где
определено с помощью К04 ПДС, а PvB
- расстояние от точки В до постоянного
центра вращения звена).
(где
определено с помощью К04 ПДС, а PvB
- расстояние от точки В до постоянного
центра вращения звена).
К.8
Изображаются на рисунке ускорения
![]() .
Если направления ускорений
.
Если направления ускорений![]() или
или![]() неизвестны, то рисую-тся их составляющие
после проектирования на те или иные
оси.
неизвестны, то рисую-тся их составляющие
после проектирования на те или иные
оси.
К.9 Выбираются
оси декартовой системы координат (х, у)
или естественные оси (![]() )
так, чтобы по возможности после
проектирования соотношения уровня5
на эти оси, хотя бы в одно из двух уравнений
входил только один неизвестный
кинематический параметр. В некоторых
частных случаях может получиться всего
одно уравнение с одним неизвестным
кинематическим параметром.
)
так, чтобы по возможности после
проектирования соотношения уровня5
на эти оси, хотя бы в одно из двух уравнений
входил только один неизвестный
кинематический параметр. В некоторых
частных случаях может получиться всего
одно уравнение с одним неизвестным
кинематическим параметром.
К.11
Соотношение
уровня 5
позволяет также решить задачу определения
и
звена, если известны ![]() и
и
![]() (условно обратная задача задаче
определения
(условно обратная задача задаче
определения![]() ,
если известны,
и
,
если известны,
и![]() ).
).
Пример 6
2
В механизме, рассмотренном в примере
5 (рис. 48), кривошип вращается с угловым
ускорением
![]() .
.
Н
В
примере 5 найдены: 1=2c-1,
2=2c-1,
3=1c-1,
4=![]() c-1,
5=
c-1,
5=![]() c-1.
c-1.![]() в рассматриваемый момент времени,
используя условия примера 5.
в рассматриваемый момент времени,
используя условия примера 5.
3
 К04 ПДС
К04 ПДС
1... 5
4 n=5.
=1
![]()
![]()
5
 К03 ВДТ
К03 ВДТ
![]()
Ускорение
![]() направлено по кривошипу
направлено по кривошипу![]() В12
в сторону
В12
в сторону ![]() ,
,
![]() (рис.
50)
(рис.
50)

Рис. 50
=2
Так как для точки, общей для второго и третьего звеньев – B23, неизвестно ускорение ни по величине, ни по направлению и неизвестно 2, то, с учетом комментария 5, сначала используется теорема об ускорениях точек плоской фигуры для точек B12 и D2 (точка типа – П) второго звена, а затем для точек второго звена B12 и B23.
Точки B12 и D2 второго звена.
![]() .
.
|
6 |
2 |
2 |
|
|
|
7 |
Определено в 3 2=2c-1. |
Не
дано, нельзя определить,
|
Не дано. |
Не дано. |
|
8 |
|
Неизвестно
известно направление
|
Общая точка с предыдущим звеном
|
Точка
типа - П, известно только направление
Неизвестно
|
Ускорения изображены на рис. 50.
9 Ось х - горизонтальна, ось у - вертикальна. Проекции соотношения 5 для точек B12 и D2 второго звена на эти оси имеют вид:

10 Из
первого уравнения: ![]() ;
;
из
второго уравнения: ![]()
11 2 - известно, 2 - неизвестно
![]()
5 Точки B12 и B23 второго звена.
![]() .
.
|
6 |
2 |
2 |
|
|
|
7 |
Опред. в 3 2=2c-1. |
Опред. в 11 2=3c-2. |
Не дано. |
Не дано. |
|
8 |
B12B23 к B12. |
|
Общая точка с предыдущим звеном
|
Точка не типа - П, К, С, Неизвестны величина
и направление
|
Ускорения изображены на рис. 50.
9 Ось х - горизонтальна, ось у - вертикальна. Проекции соотношения 5 для точек B12 и B23 второго звена на эти оси имеют вид:

10 Из
первого уравнения:
![]() ,
,
из
второго уравнения:
![]()
11 2, 2 - известны.
=3
5 Точки B23 и B345 третьего звена.
![]() .
.
|
6 |
3 |
3 |
|
|
|
7 |
Определено в 3 3=1c-1. |
Не
дано, нельзя определить,
|
Не дано. |
Не дано. |
|
8 |
B23B345 к B23. |
Неизвестно
известно направление
|
Общая точка с предыдущим звеном
|
Точка
типа — К, известны направл.
|
Ускорения изображены на рис. 50.
9 Ось х - горизонтальна, ось у - вертикальна. Проекции соотношения 5 для точек B23 и B345 третьего звена на эти оси имеют вид:

10 Из
первого уравнения: ![]()
из
второго уравнения: ![]()
11 3 - известно, 3 - неизвестно
![]() .
.
=4
5 Точки B345 и D4 четвертого звена.
![]() .
.
|
6 |
4 |
4 |
|
|
|
7 |
Определено
в 3
4= |
Не
дано, можно определить,
|
Не дано. |
Не дано. |
|
8 |
направлено по B345D4 к B345. |
|
Общая точка с предыдущим звеном
направления
|
Точка не типа - П, К, С. Неизвестны величина
и направл.
|
Ускорения изображены на рис. 50.
9 Ось х - горизонтальна, ось у - вертикальна. Проекции соотношения 5 для точек B345 и D4 четвертого звена на оси x и y имеют вид:

10 ![]() ,
,
![]()
11 4, 4 - известны.
=5
 .
.

5 К03 BДТ
5
12 Ответ:
![]()


 известны
направления
известны
направления

 известны
направления
известны
направления
 Неизвестно
Неизвестно
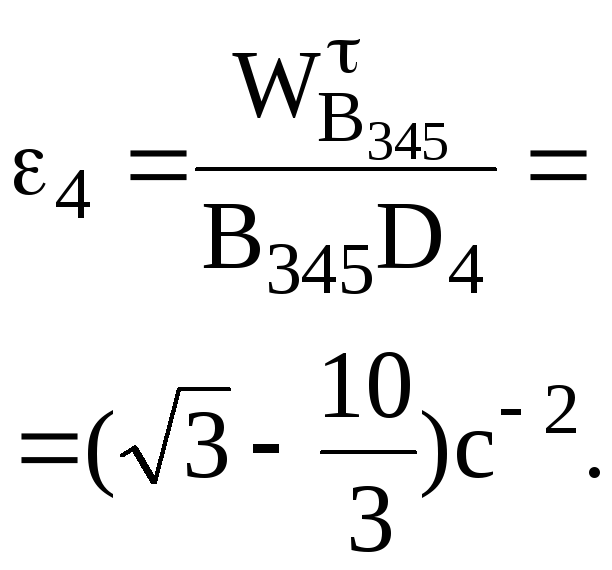


 известны
известны