Пример 1

2. К вершинам прямоугольного параллелепипеда приложена система сил, как указано на рис. 32. Привести систему сил, действующих на прямоугольный параллелепипед, к простейшей системе, если а=3м, b=4м, с=5м, =,Н,=10Н,Н,20Н,.

Выбрав систему координат, как указано на рис. 32, приведем систему сил к центру О, предварительно определив:

(т.к. ),

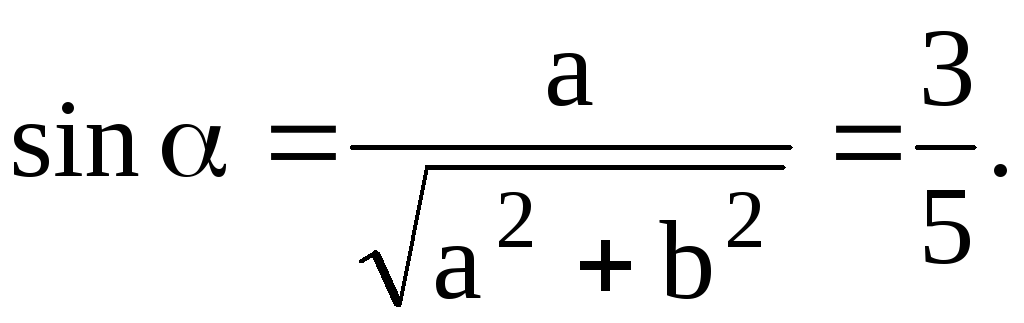
Рис. 32

3.

Н.

4. Нм,

5. ==14,14 Н,

=105,78 Нм.

6.

7. .

8. .

9. Динама

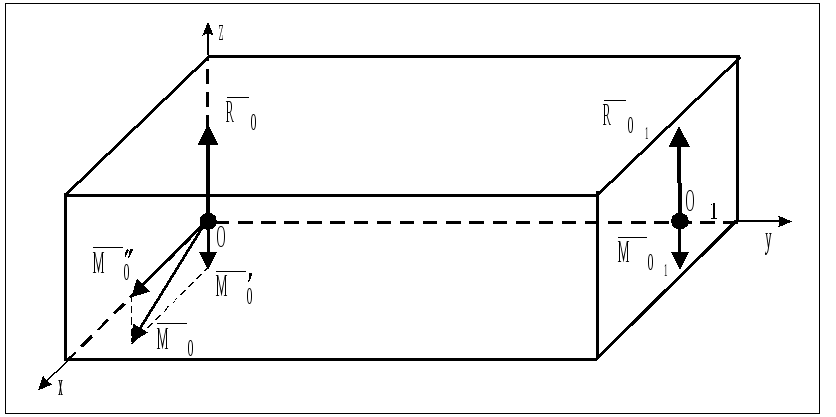
Рис. 33

, ,

,

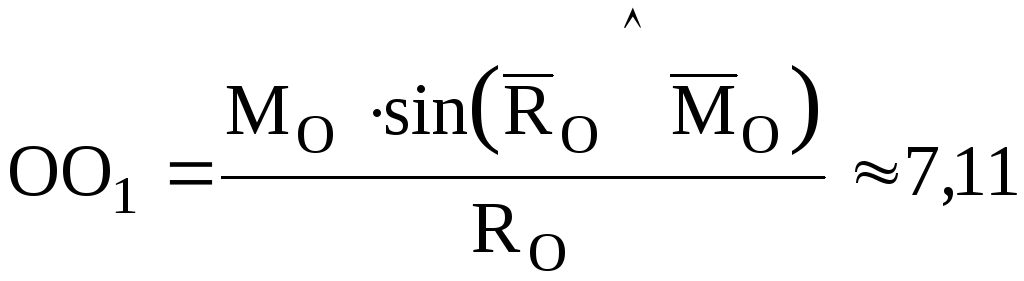м.

4.8. Теорема Вариньона

4.8.1. Пространственная система сил

Теорема: Если пространственная система сил имеет равнодействующую, то момент этой равнодействующей относительно любой точки равен геометрической сумме моментов всех сил этой системы относительно той же точки:

. (4.29)

Доказательство: Пусть система сил приводится к равнодействующей, которая приложена в точке О, тогда, используя основную теорему статики, получим:

' ,

где на основании (4.2) .

С другой стороны, приведя пространственную систему сил к центру О₁ на основании соотношения (4.6) получим:

.

Сравнивая оба выражения, можно записать, с учетом соотношения (4.4):

, что и требовалось доказать.

4.8.2. Плоская система сил

Теорема: Если плоская система сил имеет равнодействующую, то величина момента равнодействующей относительно любой точки, лежащей в плоскости действия сил, равна алгебраической сумме величин моментов всех сил этой системы относительно той же точки:

. (4.30)

200