Глава 4. Приведение пространственной

и плоской систем сил

4.1. Основная теорема статики или теорема о параллельном переносе силы

Теорема: Силу, приложенную в некоторой точке НМС, не изменяя ее действия на НМС, можно переносить параллельно самой себе в любую другую точку НМС, добавляя при этом пару сил (присоединенная пара) с моментом, равным моменту силы относительно новой точки ее приложения (рис. 24).

Доказательство: Сила приложена в точке О₁. Добавив уравновешенную систему двух сил, приложенных в произвольной точке О₂, равных по модулю и параллельных силе , получим:

,

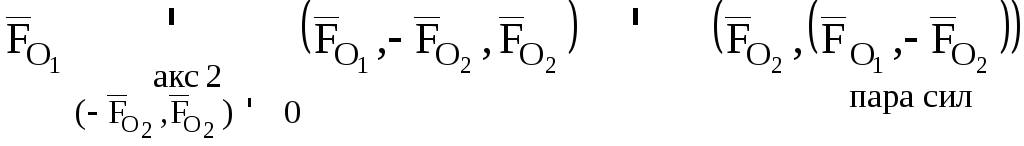, (4.1)

,

. (4.2)

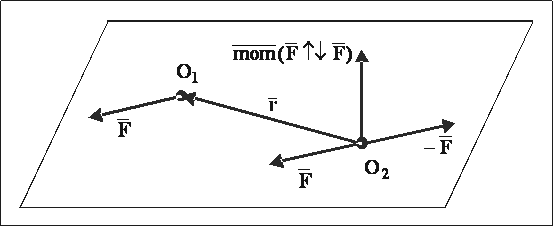
Рис. 24

4.2. Приведение систем сил к центру

4.2.1. Пространственная система сил

Пусть имеется произвольная пространственная система сил . Используя основную теорему статики, перенесем все силы системы параллельно самим себе в произвольный центр О (рис. 25):

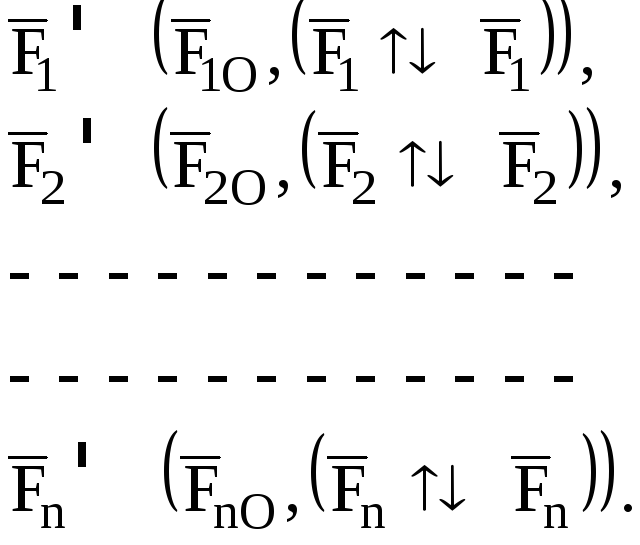
В результате получим:

система сходящихся система пар

сил в точке О

Рис. 25

Система сходящихся сил (глава 2) приводится к одной силе:

,

где на основании соотношения (2.1) можно записать:

. (4.3)

Система пар (глава 3) приводится к одной паре:

момент которой на основании соотношений (3.10), (4.2) и (1.2) определится формулой:

. (4.4)

Итак,

(4.5)

или условно можно записать:

. (4.6)

Таким образом, произвольная система сил всегда может быть приведена в произвольно выбранной точке – центре приведения к силе, равной геометрической сумме всех сил и называемой ее главным вектором, и к паре сил с моментом, равным геометрической сумме моментов всех сил системы относительно центра приведения и называемым ее главным моментом.

4.2.2. Плоская система сил

Пусть имеется плоская система сил . Взяв в качестве центра приведения произвольную точку на плоскости действия сил, можно сделать следующие выводы, учтя, что все моменты сил, лежащих в одной плоскости, относительно точки плоскости перпендикулярны этой плоскости:

Главный вектор плоской системы сил всегда лежит в плоскости действия сил (рис. 26).

Главный момент равен по величине алгебраической сумме величин моментов сил относительно центра приведения и перпендикулярен плоскости действия сил (рис. 26).

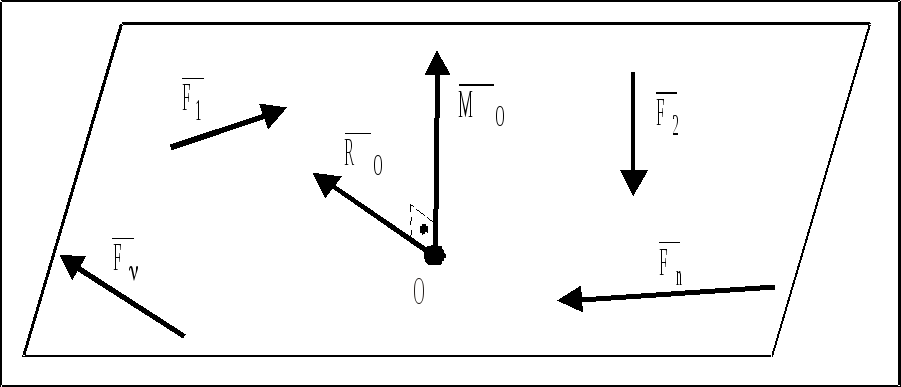
Рис. 26

, (4.7) . (4.8)

, (здесь ) (4.9)

.

4.3. Формулы для нахождения главного вектора и главного момента

4.3.1. Пространственная система сил

Проектируя соотношение (4.3) на оси декартовой системы координат с началом в центре приведения, получим проекции главного вектора пространственной системы сил на эти оси:

(4.10)

Модуль главного вектора и его направляющие косинусы определяются по известным формулам векторного анализа:

, (4.11)

(4.12)

Проектируя соотношение (4.4) на оси декартовой системы координат с учетом связи между моментом силы относительно точки и оси, получим проекции главного момента пространственной системы сил на эти оси:

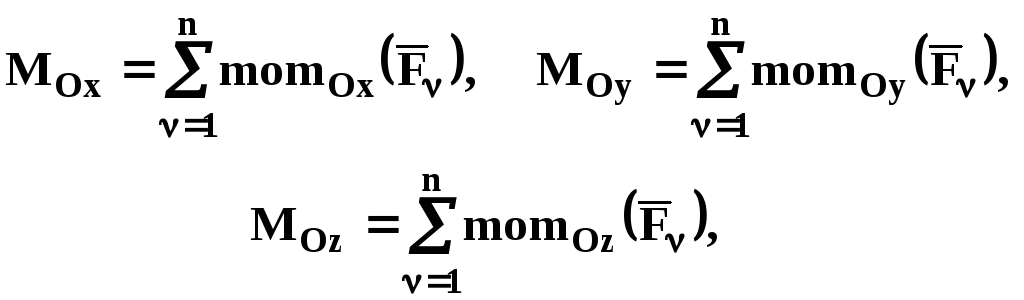(4.13)

где – моменты силыотносительно осей декартовой системы координат.

Модуль главного момента и его направляющие косинусы определяются по известным формулам векторного анализа:

. (4.14)

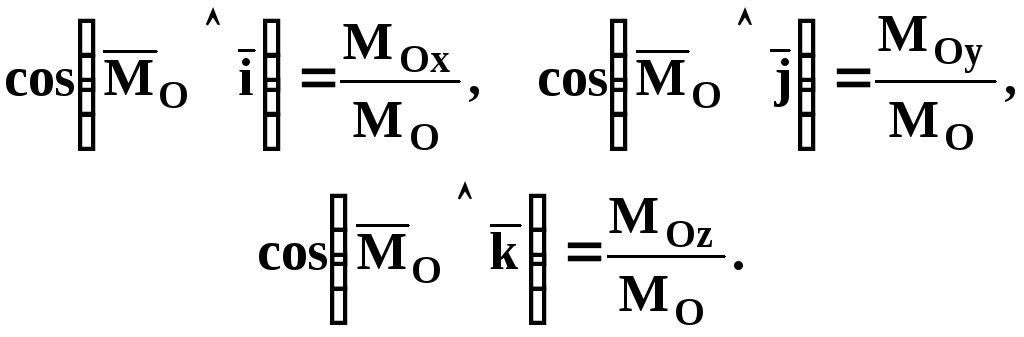(4.15)