4_семестр_Лекция_№22

6

Лекция 22.

Числовые характеристики выборки. Статистики и точечные оценки.

Методы моментов, максимального правдоподобия и наименьших квадратов

По результатам выборочных наблюдений вычисляются статистические числовые характеристики: выборочное среднее, выборочная дисперсия, выборочное среднее квадратическое отклонение, выборочный коэффициент корреляции и т. д. Эти характеристики определяют соответствующие параметры генеральной совокупности. Выборочные характеристики, являясь случайными величинами, зависящими от выборки, оценивают параметры случайной величины из генеральной совокупности.

Пусть – выборка из генеральной совокупности случайной величины .

Средним значением выборки или выборочным средним называется число , равное

,

если все варианты выборки объема различны, и

,

если варианты имеют соответствующие частоты , причем .

Число – называется отклонением величины от выборочного среднего .

Если все варианты выборки объема различны, то выборочной дисперсией называется число , равное

,

а если варианты имеют соответствующие частоты , причем , то

.

Следовательно, выборочная дисперсия равна среднему арифметическому квадратов наблюдаемых отклонений.

Выборочную дисперсия можно записать также в виде

.

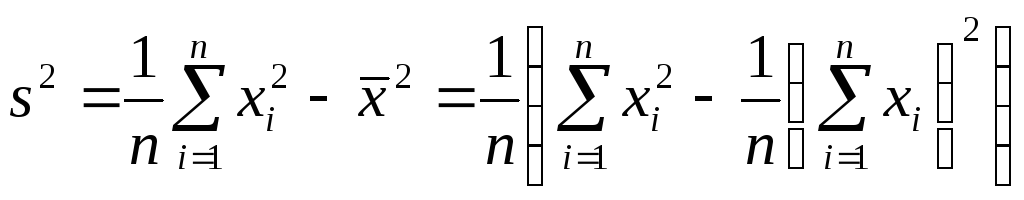Если варианты выборки имеют соответствующие частоты , , и , то выборочная дисперсия приводится к виду

.

Часто в математической статистике применяется модифицированная дисперсия , равная

или

.

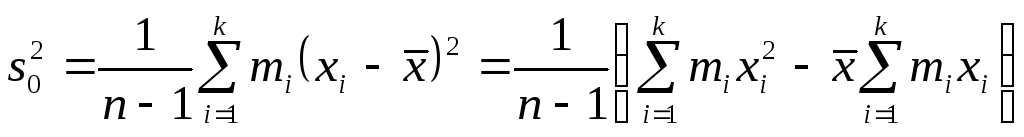Модифицированная дисперсия связана с выборочной дисперсией соотношением

.

Корень квадратный из выборочной дисперсии называется выборочным средним квадратическим отклонением .

Простейшей мерой рассеяния случайной величины является размах выборки – разность между наибольшим и наименьшим значениями выборки: .

Характеристики вида

; ,

называются соответственно -м центральным и начальным выборочными моментами соответственно. Заметим, что , .

Если в генеральной совокупности рассматриваются одновременно два признака и , например, рост и масса человека в данной группе людей, то для характеристики их взаимосвязи вводится понятие выборочной ковариации :

.

Здесь , – отдельные значения в соответствующих выборках. После несложных преобразований получим

,

где – выборочное среднее произведения случайных величин и .

Ковариация может быть положительной, отрицательной или равной нулю. Если большим (малым) значениям соответствуют большие (малые) значения , то . Говорят, что в этом случае между признаками и существует положительная корреляция. В противном случае говорят, что между признаками и существует отрицательная корреляция. При между признаками и корреляция отсутствует.

Отметим некоторые свойства выборочного среднего и выборочной дисперсии в виде теорем.

Теорема. Сумма отклонений отдельных вариант выборки от их выборочного среднего равна нулю: .

Теорема. Пусть – случайная выборка случайной величины , причем , , . Тогда для случайной величины имеем

, .

Следствие. Если – случайная выборка случайной величины , нормально распределенной по закону , то случайная величина имеет нормальное распределение .

Такие распределения, как биноминальное, показательное, нормальное, являются семействами распределений, зависящими от одного или нескольких параметров. Например, показательное распределение с плотностью вероятностей , , зависит от одного параметра , нормальное распределение – от двух параметров и . Из условий исследуемой задачи, как правило, ясно, о каком семействе распределений идет речь. Однако остаются неизвестными конкретные значения параметров этого распределения, входящих в выражения функции распределения вероятностей. Поэтому возникает задача нахождения этих параметров.

Пусть закон распределения генеральной совокупности определен с точностью до значений входящих в его распределение параметров , часть из которых может быть известна. Одной из задач математической статистики является нахождение оценок неизвестных параметров по выборке наблюдений из генеральной совокупности. Оценка неизвестных параметров заключается в построении функции от случайной выборки, такой, что значение этой функции приближенно равно оценивающему неизвестному параметру . Функцию называют статистикой, а значение этой функции – точечной оценкой параметра . Например, выборочное среднее и медиана могут служить оценкой среднего значения всей генеральной совокупности, выборочная дисперсия – дисперсии этой совокупности.

Существует два вида оценок – точечные и интервальные. Точечная оценка параметра определяется одним числом . При малом числе наблюдений эти оценки могут приводить к грубым ошибкам. Чтобы избежать их, используют интервальные оценки, которые определяются двумя числами и – границами интервала, в котором с заданной вероятностью заключена оцениваемая величина .

Для данного неизвестного параметра может существовать несколько статистик, вполне подходящих для того, чтобы служить оценками. Например, выборочное среднее , мода и медиана могут показаться вполне пригодными для оценивания среднего значения всей генеральной совокупности. Выбор «наилучших» оценок определяется их несмещенностью, эффективностью и состоятельностью.

Оценка параметра называется несмещенной (без систематических ошибок), если математическое ожидание оценки совпадает с истинным значением :

.

Если это равенство не имеет места, то оценка называется смещенной (с систематическими ошибками). Это смещение может быть связано с ошибками измерения, счета или неслучайным характером выборки. Систематические ошибки приводят к завышению или занижению оценки.

Выборочное среднее является несмещенной оценкой математического ожидания .

Пусть , . Выберем в качестве оценки дисперсии выборочную дисперсию , где , – варианты выборки случайной величины . Найдем математическое ожидание этой оценки. Преобразуем, вначале, случайную величину к удобному виду

.

Итак,

.

В силу независимости случайных величин имеем

,

то есть

,

и, следовательно, выборочная дисперсия является смещенной оценкой дисперсии .

Однако несмещенной оценкой дисперсии является . Таким образом, модифицированная выборочная дисперсия является несмещенной оценкой дисперсии .

Для некоторых задач математической статистики может существовать несколько несмещенных оценок. Обычно предпочтение отдают той, которая обладает наименьшим рассеянием (дисперсией).

Несмещенная оценка параметра , обладающая минимальной дисперсией среди всех несмещенных оценок для , называемая эффективной.

Пусть – минимальная дисперсия, а – дисперсия любой другой несмещенной оценки параметра . Тогда по определению эффективность оценки равна 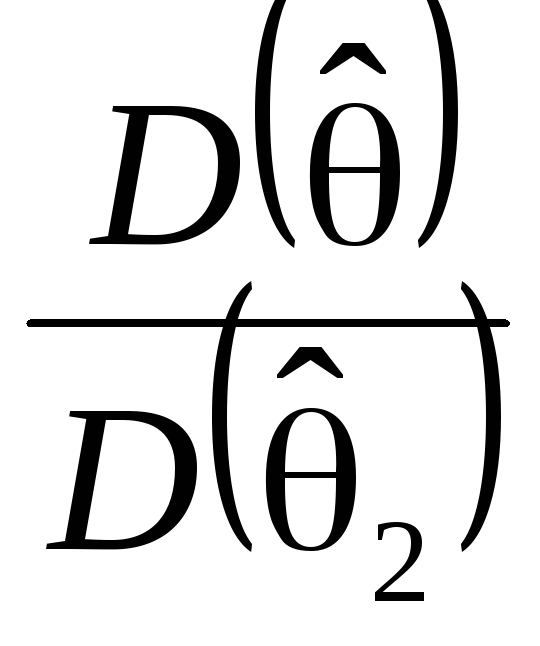. Ясно, что .

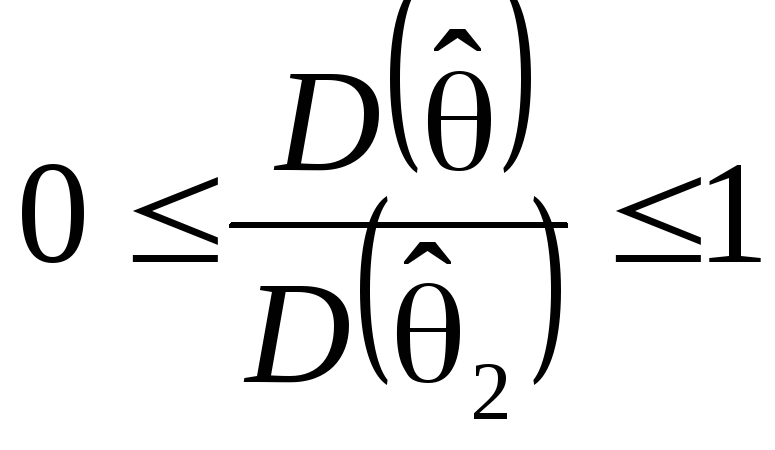Часто оценка становится эффективной с увеличением объема выборки. Предельная эффективность оценки при называется асимптотической эффективностью. Если асимптотическая эффективность равна единице, оценка называется асимптотически эффективной.

Выборочное среднее – эффективная оценка, а оценка является асимптотически эффективной.

Замечание. Если оценка смещенная, то малость ее дисперсии еще не говорит о малости ее погрешности. Взяв, например, в качестве оценки параметра некоторое число , получим оценку даже с нулевой дисперсией. Однако в этом случае ошибка (погрешность) может быть сколь угодно большой.

Оценка называется состоятельной или асимптотически состоятельной, если с увеличением объема выборки оценка сходится по вероятности к точному значению параметра , то есть для любого

.

Состоятельность оценки параметра означает, что с ростом объема выборки качество оценки улучшается.

Точечные оценки , и есть состоятельные оценки.

Универсального метода нахождения несмещенных, эффективных и состоятельных точечных оценок параметров распределения случайной величины не существует. Имеется несколько хорошо зарекомендовавших себя методов нахождения этих оценок. Рассмотрим некоторые из них.

1) Метод моментов (Пирсона). Пусть известен закон распределения случайной величины , содержащий неизвестные параметры . Произведем выборку объема этой случайной величины. По методу моментов выборочных моментов приравниваются к первым моментам случайной величины . Из полученной системы уравнений и находим оценки параметров . Как правило, эти оценки состоятельны.

Теоретическим обоснованием метода моментов служит закон больших чисел, согласно которому для рассматриваемого случая при большом объеме выборки выборочные моменты близки к истинным моментам генеральной совокупности. Например, пусть – случайная величина, распределенная по нормальному закону . Известно, что – начальный момент первого порядка, а – центральный момент второго порядка, которые согласно формуле (6.3.10) можно оценить выборочным начальным моментом первого порядка и выборочным центральным моментом второго порядка соответственно. Тем самым по методу моментов неизвестное математическое ожидание оценивается средним арифметическим , а дисперсия – выборочной дисперсией .

2) Метод максимального правдоподобия. Этот метод разработан Фишером. Оценки, получаемые с его помощью, как правило, являются наиболее надежными и особенно предпочтительны в случае малого числа наблюдений.

Метод максимального правдоподобия состоит в определение оценок , максимизирующих функцию правдоподобия . Функция правдоподобия строится следующим образом. Пусть результаты наблюдений случайных величин , совместное распределение вероятностей которых зависит от неизвестных параметров , то есть представляет собой условную вероятность . Условное совместное распределение вероятностей случайных величин называется функцией правдоподобия. При фиксированных значениях выборки функция правдоподобия является только функцией неизвестных параметров, то есть

.

По методу максимального правдоподобия в качестве оценок для выбираются такие значения , при которых «наблюдаемые» величины наиболее вероятны, другими словами, значения максимизируют функцию правдоподобия .

Пусть, например, – дискретная случайная величина и , – ее закон распределения вероятностей. Тогда вероятность того, что элементы выборки (независимые случайные величины ) примут конкретные значения , определяется равенством

.

Поскольку эта функция определяет совместное распределение вероятностей, то, следовательно, она является функцией правдоподобия. Таким образом, для дискретной случайной величины с законом распределения функция правдоподобия определяется соотношением

.

При оценке параметров распределения непрерывной случайной величины с плотностью распределения вероятностей функция правдоподобия определяется следующим образом:

.

Оценка параметров , построенная по выборочным значениям случайной величины и максимизирующая функцию , называется оценкой максимального правдоподобия.

Для упрощения вычислений оценок максимального правдоподобия удобно рассматривать логарифм функции правдоподобия, то есть , который в силу монотонности логарифма не изменяет точки максимума самой функции.

При максимизации функции величины , считают фиксированными, а оценки максимального правдоподобия параметров определяются из системы уравнений

, ,

или системы

, .

Эти системы называются системами уравнений правдоподобия.

Замечание. Метод максимального правдоподобия не всегда дает оценки, удовлетворяющие требованиям несмещенности, эффективности и состоятельности. Поэтому к оценкам, получаемым этим методом, следует относиться критически. Кроме того, метод максимального правдоподобия не всегда удается применить даже в простых случаях.

3) Метод наименьших квадратов. Пусть требуется измерить некоторую величину по результатам измерений , , где – ошибки измерений, а – точное значение измеряемой величины.