
4_семестр_Лекция_№25
.doc
Лекция 25.
Критерии значимости. Критерий согласия Пирсона. Регрессионный анализ
Пусть случайная
величина
![]() имеет нормальное распределение
имеет нормальное распределение
![]() и из генеральной совокупности извлечена
выборка
и из генеральной совокупности извлечена
выборка
![]() ,
то есть известна одна из реализаций
случайной выборки
,
то есть известна одна из реализаций
случайной выборки
![]() .
Рассмотрим для этого случая различные
критерии значимости.
.
Рассмотрим для этого случая различные
критерии значимости.
1. Критерии
значимости для основной гипотезы
![]() при известном значении дисперсии
при известном значении дисперсии
![]() .
Для проверки гипотезы
.
Для проверки гипотезы
![]() .
при заданном уровне значимости
.
при заданном уровне значимости
![]() можно выбрать одну из следующих
альтернативных гипотез:
можно выбрать одну из следующих
альтернативных гипотез:
![]() ,
,
![]() ,
,
![]() .
При истинной гипотезе
.
При истинной гипотезе
![]() статистика
статистика
![]()
имеет стандартное
(нормированное) нормальное распределение
![]() .
.
Тогда в соответствии
с правилами принятия основной гипотезы
![]() ,
изложенными в п. 6.8, области
,
изложенными в п. 6.8, области
![]() ,
,
![]() и
и
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() ,
,
![]() – квантили распределения
– квантили распределения
![]() ,
являются критическими для соответствующих
альтернативных гипотез
,
являются критическими для соответствующих
альтернативных гипотез
![]() ,
,
![]() или
или
![]() .
Отсюда если для данной выборки
.
Отсюда если для данной выборки
![]() оказалось, что
оказалось, что
![]() ,
,
![]() ,
,
или
![]() ,
,
то принимается
гипотеза
![]() для соответствующих альтернативных
гипотез
для соответствующих альтернативных
гипотез
![]() ,
,
![]() или
или
![]() .
В противном случае основная гипотеза
.
В противном случае основная гипотеза
![]() отвергается с уровнем значимости
отвергается с уровнем значимости
![]() как не согласующаяся с опытом, но
принимается соответствующая альтернативная
гипотеза
как не согласующаяся с опытом, но
принимается соответствующая альтернативная
гипотеза
![]() .
.
2. Критерии
значимости для основной гипотезы
![]() при неизвестном значении дисперсии
при неизвестном значении дисперсии
![]() .
В этом случае в качестве статистики
используют случайную величину
.
В этом случае в качестве статистики
используют случайную величину
![]() ,
,
где
![]() ,
которая, если верна гипотеза
,
которая, если верна гипотеза
![]() ,
имеет
,
имеет
![]() -
распределение Стьюдента с числом
степеней свободы
-
распределение Стьюдента с числом
степеней свободы
![]() ,
где
,
где
![]() – объем выборки.
– объем выборки.
Если альтернативная
гипотеза имеет вид
![]() ,
то используем левостороннюю критическую
область, которая удовлетворяет следующему
условию:
,
то используем левостороннюю критическую
область, которая удовлетворяет следующему
условию:
![]() .
.
Если альтернативная
гипотеза имеет вид
![]() ,
то используем правостороннюю критическую
область
,
то используем правостороннюю критическую
область
![]() .
.
И, наконец, при
альтернативной гипотезе
![]() используем двустороннюю критическую
область
используем двустороннюю критическую
область
![]() .
.
В этих неравенствах
![]() – выборочное значение статистики
– выборочное значение статистики
![]() ;
;
![]() ,
,
![]() ,
,
![]() ,
,
![]() – квантили распределения Стьюдента;
– квантили распределения Стьюдента;
![]() – уровень значимости.
– уровень значимости.
3. Критерии
значимости для основной гипотезы
![]() при известном значении
при известном значении
![]() математического ожидания. Выберем
статистику
математического ожидания. Выберем
статистику
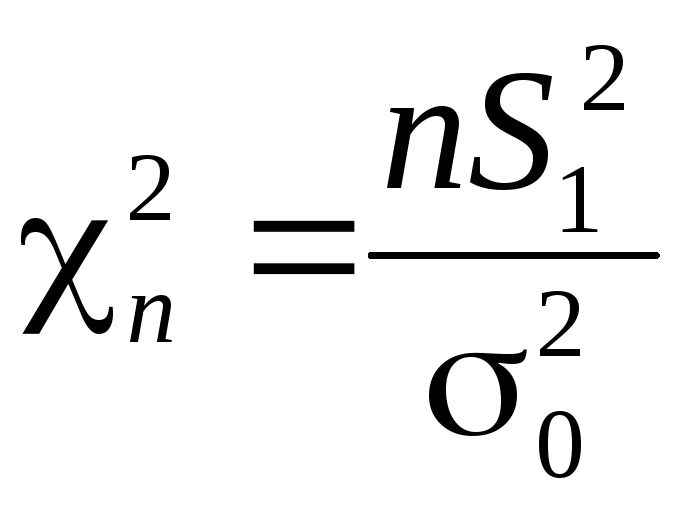 ,
,
где, по прежнему,
![]() – объем случайной выборки
– объем случайной выборки
![]() ;
;
![]() .
Случайная величина
.
Случайная величина
![]() имеет
имеет
![]() -
распределение с
-
распределение с
![]() степенями свободы. Отсюда, если
альтернативная гипотеза имеет вид
степенями свободы. Отсюда, если
альтернативная гипотеза имеет вид
![]() ,
то применяем левостороннюю критическую
область
,
то применяем левостороннюю критическую
область
![]() .
.
Если альтернативная
гипотеза имеет вид
![]() ,
то используем правостороннюю критическую
область
,
то используем правостороннюю критическую
область
![]() .
.
В случае же
альтернативной гипотезы
![]() применяем двустороннюю критическую
область
применяем двустороннюю критическую
область
![]() .
.
Здесь
 – выборочное значение статистики
– выборочное значение статистики
![]() ;
;
![]() ,
,
![]() ,
,
![]() ,
,
![]() – квантили
– квантили
![]() -
распределения;
-
распределения;
![]() – уровень значимости.
– уровень значимости.
4. Критерии
значимости для основной гипотезы
![]() при неизвестном значении
при неизвестном значении
![]() математического ожидания. Воспользуемся
статистикой
математического ожидания. Воспользуемся
статистикой
 ,
где
,
где
![]() – объем случайной выборки
– объем случайной выборки
![]() ;
;
![]() .
Если гипотеза
.
Если гипотеза
![]() верна, то случайная величина
верна, то случайная величина
![]() имеет
имеет
![]() -
распределение с
-
распределение с
![]() степенями свободы.
степенями свободы.
Если альтернативная
гипотеза имеет вид
![]() ,
находим левостороннюю критическую
область
,
находим левостороннюю критическую
область
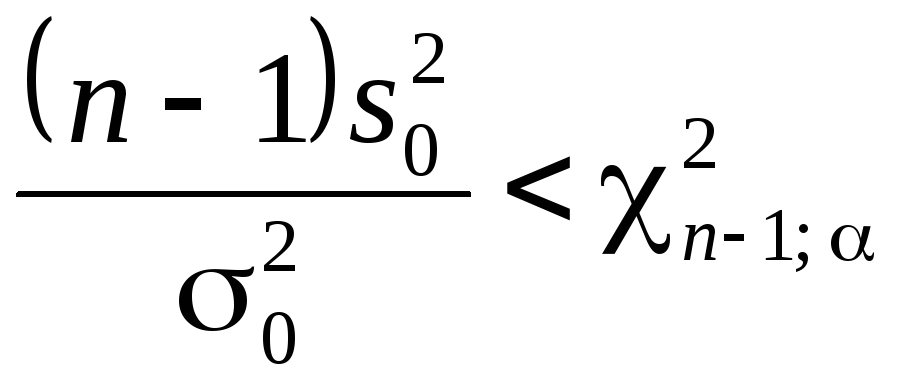 .
.
При альтернативной
гипотезе
![]() находим правостороннюю критическую
область
находим правостороннюю критическую
область
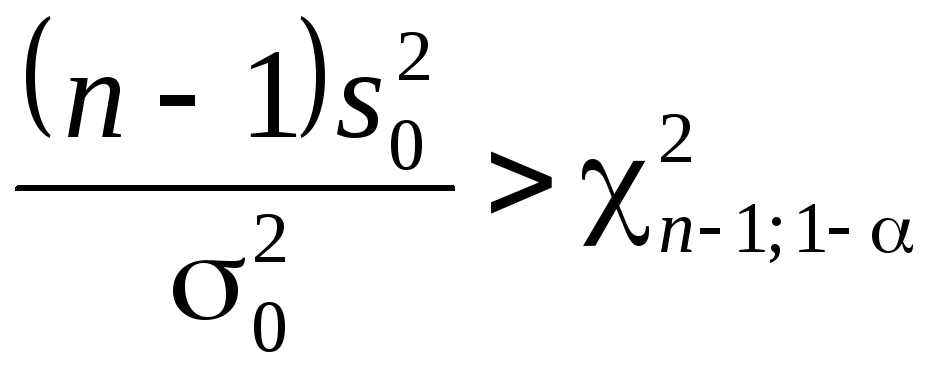 .
.
При альтернативной
гипотезе
![]() находим двустороннюю критическую
область
находим двустороннюю критическую
область
 .
.
Рассмотрим теперь задачу проверки гипотезы о равенстве двух математических ожиданий. Эта задача имеет важное практическое значение, поскольку выборочное среднее одной выборки может отличаться от выборочного среднего другой выборки из одной и той же генеральной совокупности.
Пусть
![]() и
и
![]() – две случайные выборки из генеральных
совокупностей
– две случайные выборки из генеральных
совокупностей
![]() и
и
![]() соответственно, имеющие нормальный
закон распределения. Пусть дисперсии
случайных величин
соответственно, имеющие нормальный
закон распределения. Пусть дисперсии
случайных величин
![]() и
и
![]() известны и равны соответственно
известны и равны соответственно
![]() и
и
![]() .
Проверим нулевую гипотезу о равенстве
математических ожиданий случайных
величин
.
Проверим нулевую гипотезу о равенстве
математических ожиданий случайных
величин
![]() и
и
![]() ,
то есть гипотезу
,
то есть гипотезу
![]() .
В этом случае альтернативная гипотеза
.
В этом случае альтернативная гипотеза
![]() означает, что
означает, что
![]() .
.
Наилучшие оценки
математических ожиданий
![]() и
и
![]() равны выборочным средним
равны выборочным средним
![]() и
и
![]() ,
причем случайные величины
,
причем случайные величины
![]() и
и
![]() имеют нормальные распределения
имеют нормальные распределения
![]() и
и
![]() соответственно. Так как ничего не
известно о математических ожиданиях
соответственно. Так как ничего не
известно о математических ожиданиях
![]() и
и
![]() ,
то для проверки гипотезы
,
то для проверки гипотезы
![]() можно использовать статистики
можно использовать статистики
![]() и
и
![]() .
Из независимости выборок следует
независимость и выборочных средних
.
Из независимости выборок следует
независимость и выборочных средних
![]() и
и
![]() .
Кроме того, случайная величина
.
Кроме того, случайная величина
![]() имеет нормальное распределение
вероятностей, причем
имеет нормальное распределение
вероятностей, причем
![]() .
Если гипотеза
.
Если гипотеза
![]() верна, то
верна, то
![]() .
Отсюда следует, что случайная величина
.
Отсюда следует, что случайная величина
![]()
имеет нормальное
распределение
![]() .
.
Пусть
![]() – уровень значимости. Тогда область
– уровень значимости. Тогда область
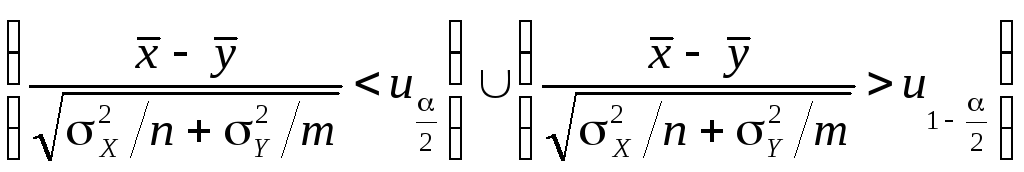
определяет
двустороннюю критическую область для
гипотезы
![]() в случае выбора альтернативной гипотезы
в случае выбора альтернативной гипотезы
![]() .
Учитывая, что
.
Учитывая, что
![]() ,
неравенство, определяющее область
принятия гипотезы
,
неравенство, определяющее область
принятия гипотезы
![]() для двустороннего критерия, можно
записать в виде
для двустороннего критерия, можно
записать в виде
![]() .
.
Критерий согласия,
как было отмечено в п. 6.8, – это
критерий, с помощью которого проверяют
гипотезу о том, что генеральная
совокупность имеет распределение
предполагаемого типа. Имеется несколько
критериев согласия: хи-квадрат, Колмогорова
– Смирнова,
![]() и др.
и др.
Критерий
![]() (Пирсона) является универсальным. Он
применим для проверки любого вида
распределения. Критерий
(Пирсона) является универсальным. Он
применим для проверки любого вида
распределения. Критерий
![]() позволяет выполнить проверку гипотезы
о соответствии опытного закона
распределения предполагаемому не только
в случаях, когда последний известен
полностью, но и тогда, когда параметры
предполагаемого закона распределения
определяются на основании опытных
данных.
позволяет выполнить проверку гипотезы
о соответствии опытного закона
распределения предполагаемому не только
в случаях, когда последний известен
полностью, но и тогда, когда параметры
предполагаемого закона распределения
определяются на основании опытных
данных.
Пусть
![]() – выборка объема
– выборка объема
![]() наблюдений случайной величины
наблюдений случайной величины
![]() .
Проверим гипотезу
.
Проверим гипотезу
![]() ,
утверждающую, что
,
утверждающую, что
![]() имеет функцию распределения
имеет функцию распределения
![]() .
.
Проверка гипотезы
![]() при помощи критерия
при помощи критерия
![]() осуществляется по следующей схеме.
осуществляется по следующей схеме.
1) По выборке
наблюдений находят точечные оценки
неизвестных параметров предполагаемого
закона распределения случайной величины
![]() .
.
2) Область возможных
значений случайной величины
![]() разбивается на
разбивается на
![]() непересекающихся интервалов
непересекающихся интервалов
![]() ,
,
![]() в случае, когда
в случае, когда
![]() – непрерывная случайная величина, или
– непрерывная случайная величина, или
![]() групп, состоящих из отдельных значений,
для дискретной случайной величины
групп, состоящих из отдельных значений,
для дискретной случайной величины
![]() .
.
3) Исходя из
предполагаемого закона распределения
случайной величины
![]() ,
находят теоретическую вероятность
,
находят теоретическую вероятность
![]() того, что значение
того, что значение
![]() принадлежит интервалу
принадлежит интервалу
![]() ,
то есть
,
то есть![]() ,
,
![]() ,
при этом
,
при этом
![]() ,
,
![]() ,
где
,
где
![]() – число элементов выборки, принадлежащих
интервалу
– число элементов выборки, принадлежащих
интервалу
![]() (эмпирическая частота попадания в
(эмпирическая частота попадания в
![]() -й
интервал).
-й
интервал).
4) Вычисляют
выборочное значение статистики критерия
![]() по формуле
по формуле
![]() .
.
Близость относительных
частот
![]() к вероятности
к вероятности
![]() свидетельствует в пользу основной
гипотезы
свидетельствует в пользу основной
гипотезы
![]() ,
заметные различия отвергают гипотезу
,
заметные различия отвергают гипотезу
![]() .
.
5) Определяют число
![]() степеней свободы распределения по
формуле
степеней свободы распределения по
формуле
![]() ,
,
где
![]() – число параметров предполагаемого
закона распределения.
– число параметров предполагаемого
закона распределения.
6) Зная число
![]() и задавая уровень значимости
и задавая уровень значимости
![]() ,
определяют критическое значение
,
определяют критическое значение
![]() :
:
![]() ,
,
где
![]() – квантиль распределения Пирсона (
– квантиль распределения Пирсона (![]() -
распределения).
-
распределения).
7) Гипотеза
![]() согласуется с результатами наблюдений
на уровне значимости
согласуется с результатами наблюдений
на уровне значимости
![]() ,
если
,
если
![]() .
.
Если же
![]() ,
то гипотеза
,
то гипотеза
![]() о виде функции распределения отклоняется
с уровнем значимости
о виде функции распределения отклоняется
с уровнем значимости
![]() .
.
Замечание. В
практических задачах интервалы
![]() ,
,
![]() выбираются таким образом, чтобы число
выбираются таким образом, чтобы число
![]() элементов выборки, попавших в эти
интервала, было не маленьким (
элементов выборки, попавших в эти
интервала, было не маленьким (![]() ,
,
![]() ).
Если в некоторых интервалах это условие
не выполняется, то их следует объединить
с соседними.
).
Если в некоторых интервалах это условие
не выполняется, то их следует объединить
с соседними.
Во время статистических наблюдений для каждого объекта в ряде случаев можно измерить значения нескольких признаков. Таким образом, получается многомерная выборка. Если многомерную выборку обработать по значениям отдельного признака, то получится обычная обработка одномерной выборки. Смысл обработки многомерных выборок состоит в том, чтобы установить связи между признаками. Будем рассматривать двумерные выборки.
Две случайные величины могут быть связаны либо функциональной зависимостью (каждому значению одной величины соответствует определенное значение другой величины), либо зависимостью другого рода, называемой статистической, либо быть независимыми.
Статистической (стохастической) называют зависимость, при которой изменение одной величины вызывает изменение распределения другой величины.
В частности, статистическая зависимость проявляется в том, что одна из величин зависит не только от данной второй, но и от ряда случайных факторов, или когда среди условий, от которых зависят и та и другая величины, имеются общие для них обеих условия; в этом случае статистическую зависимость называют корреляционной. Зависимости такого рода можно описать, например, при помощи корреляционной таблицы.
Регрессия (от
лат. regressio – обратное
движение) – зависимость среднего
значения какой-либо величины от некоторой
другой величины или от нескольких
величин. При регрессионной связи
одному и тому же значению
![]() могут соответствовать в зависимости
от случая различные значения величины
могут соответствовать в зависимости
от случая различные значения величины
![]() .
Если при каждом значении
.
Если при каждом значении
![]() наблюдается
наблюдается
![]() значений
значений
![]() случайной величины
случайной величины
![]() ,
то зависимость средних арифметических
,
то зависимость средних арифметических
![]()
от
![]() является регрессией в статистическом
понимании этого термина. Примером такого
рода зависимостей служит, в частности,
зависимость средних диаметров сосен
от их высот.
является регрессией в статистическом
понимании этого термина. Примером такого
рода зависимостей служит, в частности,
зависимость средних диаметров сосен
от их высот.
Изучение регрессии
основано на том, что случайные величины
![]() и
и
![]() с заданным совместным распределением
вероятностей связаны вероятностной
зависимостью: при каждом фиксированном
значении
с заданным совместным распределением
вероятностей связаны вероятностной
зависимостью: при каждом фиксированном
значении
![]() величина
величина
![]() является случайной величиной с
определенным (зависящим от значения x)
условным распределением вероятностей.
Регрессия величины
является случайной величиной с
определенным (зависящим от значения x)
условным распределением вероятностей.
Регрессия величины
![]() на
на
![]() определяется условным математическим
ожиданием
определяется условным математическим
ожиданием
![]() ,
вычисленным при условии, что
,
вычисленным при условии, что
![]() :
:
![]() .
.
Аналогично
определяется регрессия
![]() на
на
![]()
![]() .
.
Эти функции
называются функциями регрессии или
модельными функциями регрессии
соответственно
![]() на
на
![]() и
и
![]() на
на
![]() .
.
Уравнения
![]() ,
,
![]()
называются
уравнениями регрессии соответственно
![]() на
на
![]() и
и
![]() на
на
![]() .
Линии, определяемые этими уравнениями,
называются модельными линиями
регрессии. Они вводятся только для
непрерывных случайных величин.
.
Линии, определяемые этими уравнениями,
называются модельными линиями
регрессии. Они вводятся только для
непрерывных случайных величин.
Точность, с которой
уравнение регрессии
![]() на
на
![]() отражает изменение
отражает изменение
![]() в среднем при изменении
в среднем при изменении
![]() ,
измеряется условной дисперсией
величины
,
измеряется условной дисперсией
величины
![]() ,
вычисленной для каждого значения
,
вычисленной для каждого значения
![]() :
:
![]() .
.
Линии регрессии
обладают следующим свойством: среди
всех действительных функций
![]() минимум математического ожидания
минимум математического ожидания
![]() достигается для функции
достигается для функции
![]() ,
то есть регрессия
,
то есть регрессия
![]() на
на
![]() дает наилучшее, в указанном смысле,
представление величины
дает наилучшее, в указанном смысле,
представление величины
![]() по величине
по величине
![]() .
Это свойство используется для прогноза
.
Это свойство используется для прогноза
![]() по
по
![]() :
если непосредственно наблюдается лишь
компонента
:
если непосредственно наблюдается лишь
компонента
![]() вектора
вектора
![]() ,
то в качестве прогнозируемого значения
,
то в качестве прогнозируемого значения
![]() используют величину
используют величину
![]() .
.
Если
![]() при всех значениях
при всех значениях
![]() ,
то можно с достоверностью утверждать,
что
,
то можно с достоверностью утверждать,
что
![]() и
и
![]() связаны строгой функциональной
зависимостью. Если
связаны строгой функциональной
зависимостью. Если
![]() ни при каком значении
ни при каком значении
![]() и
и
![]() не зависит от
не зависит от
![]() ,
то говорят, что регрессия
,
то говорят, что регрессия
![]() на
на
![]() отсутствует. Аналогичным образом
определяется регрессия
отсутствует. Аналогичным образом
определяется регрессия
![]() на
на
![]() .
.
