Kuryerova_8variant__

ФГБОУ ВПО «Саратовский государственный технический университет

имени Гагарина Ю.А.»

Кафедра «Радиотехника»

Сдано на проверку Оценка защиты ____________

“ 27 ” декабря 2012г. “__”________________2012 г.

КУРСОВАЯ РАБОТА

" Статистическая обработка

результатов измерений"

По дисциплине:

«Метрология, стандартизация и сертификация»

Студентка группы МТС-41

Курьерова Н. С.

№ зач. книжки 0903009

Проверил: Скворцов А.А.

Саратов 2012 г.

Содержание

1. Цель работы

2. Задание

3. Основные теоретические сведения

4. Порядок выполнения измерений

5. Расчеты

6. Вывод

7. Список использованной литературы

8. Приложение

9. Лист замечаний

Задание для курсовой работы

Провести статистическую обработку ряда из n измерений, воспользовавшись данными таблицы. Результаты расчетов свести в приведенную ниже таблицу.

Таблица. Данные для статистической обработки ряда из n измерений

№ измерения	, Ом
1	598	0,98
2	590
3	600
4	595
5	599
6	591
7	589
8	593
9	597
10	592
11	587
12	590
13	588
14	596
15	594
16	585
17	589

Целью работы: освоение методики статистической обработки результатов прямых равноточных многократных измерений сопротивления резистора, предназначенного для аттенюатора.

Основные теоретические сведения

Абсолютная погрешность (ΔX, Δ) – отклонение результата измерения от истинного значения величины. Выражается в тех же единицах измерения, что и измеряемая величина.

ΔX=X_изм-X_ист

Предельная погрешность (разновидность абсолютной, (Δ_mX)) – это абсолютная погрешность, больше которой в данном измерительном эксперименте не может быть.

Абсолютная погрешность характеризует величину и знак полученной погрешности, но не определяет качество самого измерения.

Относительная погрешность - отношение абсолютной погрешности к тому значению, которое принимается за истинное. Выражается в долях или процентах.

Характеристикой качества измерений является точность отражающая меру близости измеряемых выражений к истинности.

Коэффициент погрешности:

Приведенная погрешность (разновидность относительной погрешности) – отношение абсолютной погрешности к некоторому нормирующему значению.

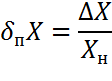
Систематическая погрешность (Δ_с) – это соответствующая погрешность измерений, которая остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины в тех же условиях.

В основу положен характер изменения во времени:

• Постоянная Δ_с

• Переменная Δ_с

Постоянная Δ_с – длительное время сохраняет свое значение (например в течении времени измерения).

Переменная Δ_с – изменяется во время процесса измерения.

• Прогрессирующая

• Периодическая

• Изменяющаяся по сложному непериодическому закону

Прогрессирующая Δ_с – монотонно возрастающая или убывающая Δ_с (как правило, изменяется по линейному закону).

Периодическая Δ_с – значение которой является периодическая функция во времени.

Изменяющаяся по сложному непериодическому закону – возникает в следствии действия нескольких систематических погрешностей.

Оценка и исключение систематической погрешности.

Систематическая погрешность () может быть связана с каждым из элементов процесса измерения: несовершенством модели объекта измерения, несовершенством метода, изменением внешних условий и т.д.

Существуют простейшие способы обнаружения и исключения :

- Исключение при измерении путём применения соответствующих методов и приёмов, например, метода замещений, метода компенсации по закону двух измерений, когда входит с разными знаками и др. Эти методы позволяют исключить , обнаружение которой представляет наибольшие трудности, непосредственно в процессе измерения, а не путём обработки результатов.

- Оценка путём применения более точного метода и средства измерения (СРИ). - - Обнаружение при измерениях с многократными наблюдениями одной физической величины двумя независимыми методами.

- Оценка расчётным путём:

где - значение измеряемой величины с учётом влияющего фактора, а - значение измеряемой величины при его отсутствии.

- Исключение путём введения поправки. Критерием целесообразности её введения является интервал суммарной погрешности измерений.

Для уменьшения в сложном приборе предусматривается возможность его калибровки с помощью внешнего или внутреннего источника калибровочного сигнала с известными параметрами.

Случайная погрешность (Δ) - составляющая погрешность измерений, при повторных измерениях одной и той же величины и в тех же условиях без видимой закономерности.

Грубая погрешность – существенно превышающая погрешность (значение) оправданная условиями измерения, свойствами измерений и квалификацией оператора.

Возникает в следствии резкого, кратковременного воздействия. Грубая погрешность определяется статистическими методами и исключается из дальнейшего измерения.

Промах – грубая погрешность в следствии неправильного действия оператора.

Оценка и исключение случайной погрешности.

Случайная погрешность () как случайная величина характеризуется плотность распределения вероятностей:

(1)

где - функция распределения.

Вероятность (Р) нахождения в заданном интервале и :

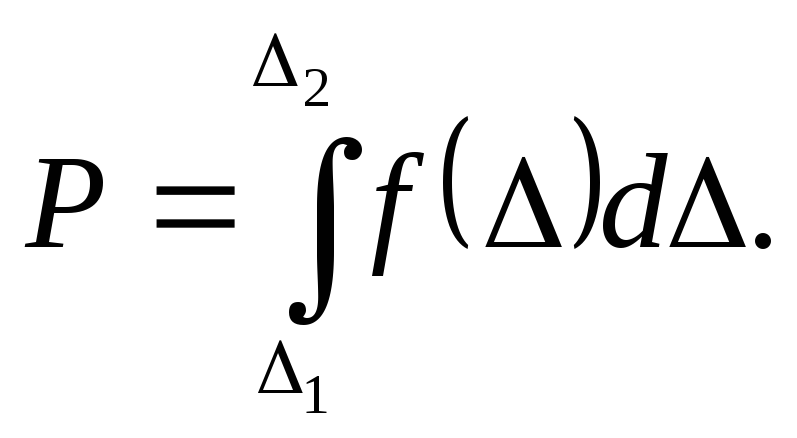
(2)

Закономерность изменения устанавливается при многократных наблюдениях ее значений и статистической обработке результатов наблюдений.

В практике электрорадиоизмерений чаще всего имеют дело с нормальным и равномерным распределением . Функция распределения по нормальному закону:

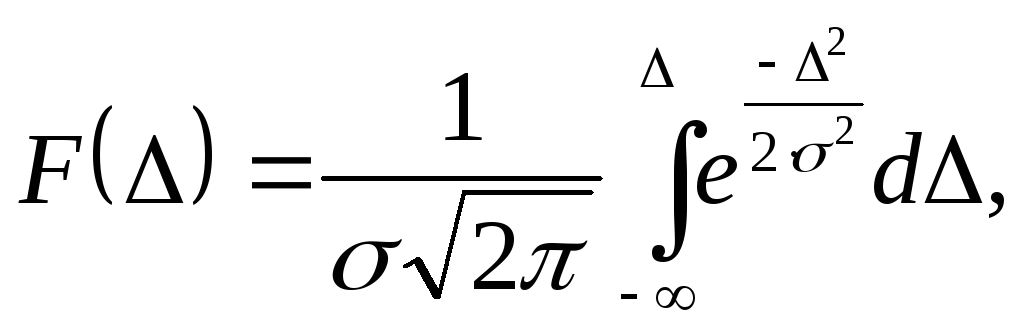
(3)

где - среднее квадратическое отклонение (СКО).

Плотность вероятности:

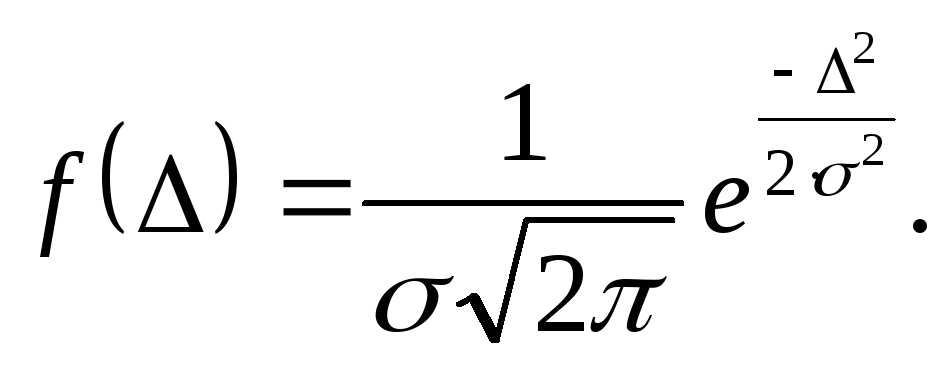
(4)

Рассмотрим процедуру статистического измерения некоторой величины, истинное значение которой.После проведения наблюдений пусть получен ряд случайных значений измеряемой величины .В каждой абсолютная погрешность.Определить невозможно, так как неизвестна .

За оценку математического ожидания (истинного значения) принимают среднее арифметическое значение:

(5)

которое называют действительным значением А измеряемой величины . Теперь можно вычислить абсолютное отклонение каждого результата наблюдений относительно среднего значения:

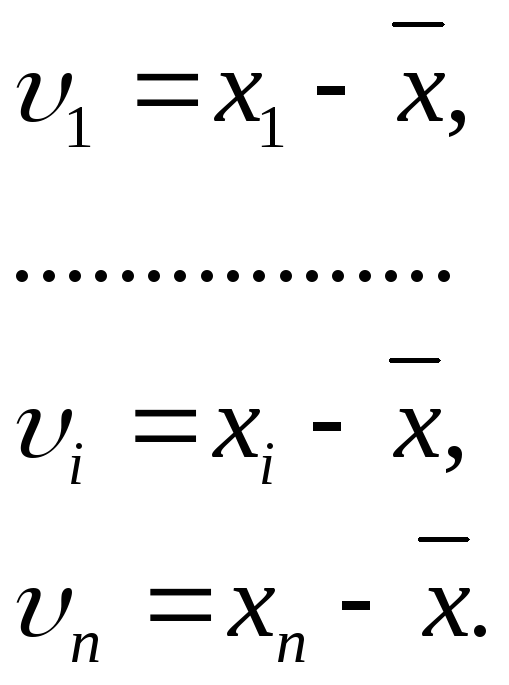
(6)

Для контроля правильности вычислений можно использовать свойства отклонений результатов наблюдений от среднего арифметического:

(7)

Оценка СКО абсолютных отклонений каждого из однократных наблюдений:

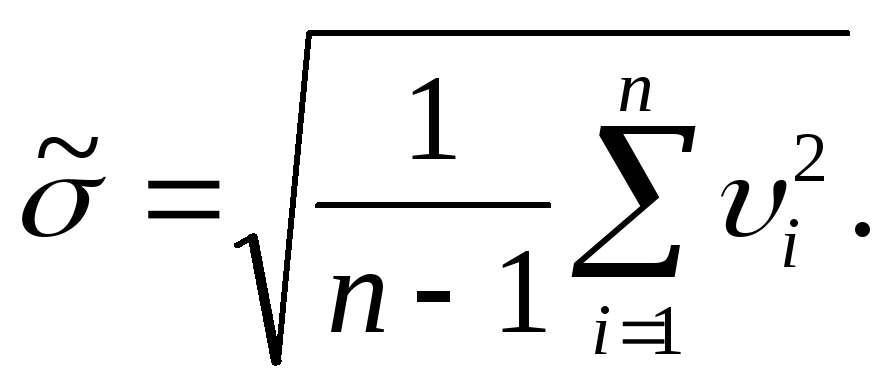
(8)

Точность результата n измерений характеризуется оценкой СКО среднего арифметического значения:

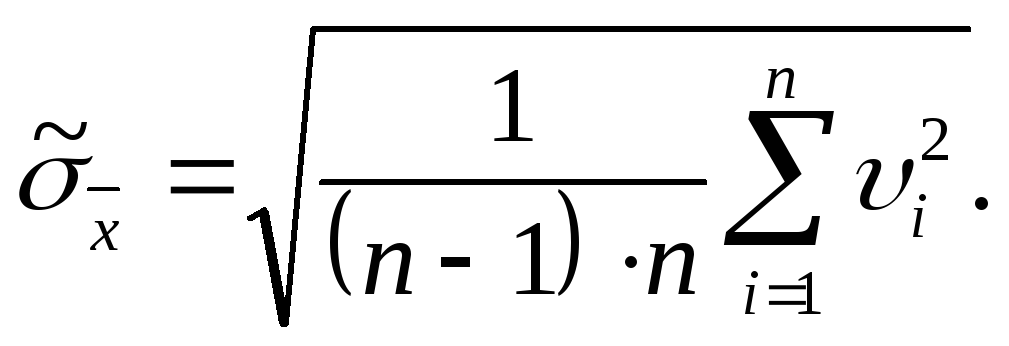
(9)

С увеличением n точность измерений возрастает.

В результате n наблюдений измерений величины получается оценка ее действительного значения А, равного среднему арифметическому. Эта оценка – также случайная величина, ее СКО определяется по формуле (9), то есть результатов измерения содержит неопределенность. Возникает вопрос о том, в каких пределах может изменяться А при статистических измерениях в одних и тех же условиях, то есть необходимо определить так называемый доверительный интервал и заданную (доверительную) вероятность. Истинное значение заключено в пределах доверительного интервала с некоторой вероятностью . В зависимости от целей измерения доверительную вероятность устанавливают равной 0,9...0,99.

Для числа наблюдений 2<n<20 доверительный интервал определяется через коэффициент ,закон изменения которого определяется распределением Стьюдента и нормированной случайной величиной:

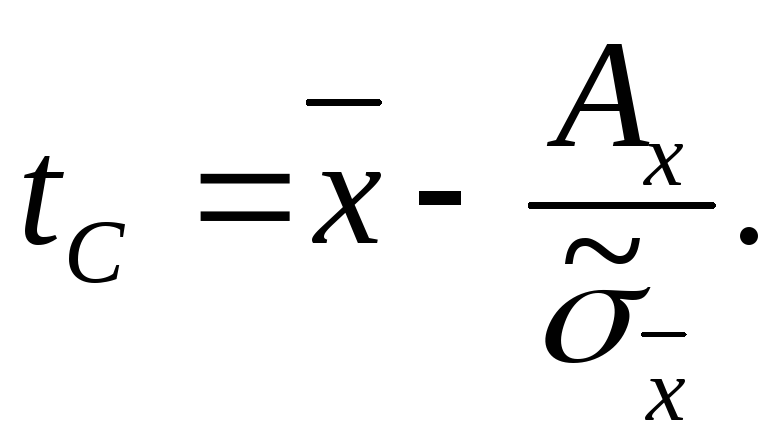
(10)

По причинам источника возникновения погрешности делятся:

• Объективные, не связанные с оператором (инструментальные, методические, внешние погрешности).

• Субъективные, обусловленные неправильными действиями оператора.

Методическая погрешность – составляющая, обусловленная несовершенством метода измерения, некорректностью алгоритмов и формул, несоответствием моделей объекта измерений, той, что правильно описывает его свойства. А так же из-за влияния средства измерения.

Инструментальная погрешность – составляющая погрешность соответствующая погрешность измерений, обусловленная несовершенством средств измерений их свойствам.

• Схемная

• Технологическая

• Эксплуатационная

Внешняя погрешность – составляющая, связанная с отклонением одной или нескольких величин влияющих на значение.

По условиям эксплуатации различают:

• Основная погрешность – погрешность средства измерения, оговоренная в документах.

• Дополнительная погрешность – выход одной из влияющих величин за пределы нормального значения.

По характеру поведения измеряемой величины во время измерения:

• Статистическая погрешность – возникает при измерении установившегося значения измеряемой величины.

• Динамическая погрешность – измеряемая величина изменяется во времени и требуется установить закон ее изменения во времени

Порядок выполнения измерений.

1) производят n наблюдений А и получают ряд ее значений ;

2) находят действительное значение А по формуле (5);

3) вычисляют ;

4) проверяют разности с целью исключения грубых погрешностей ;

5) вычисляют оценку СКО отдельных наблюдений по формуле (8);

6) определяют оценку СКО среднего арифметического по формуле (9);

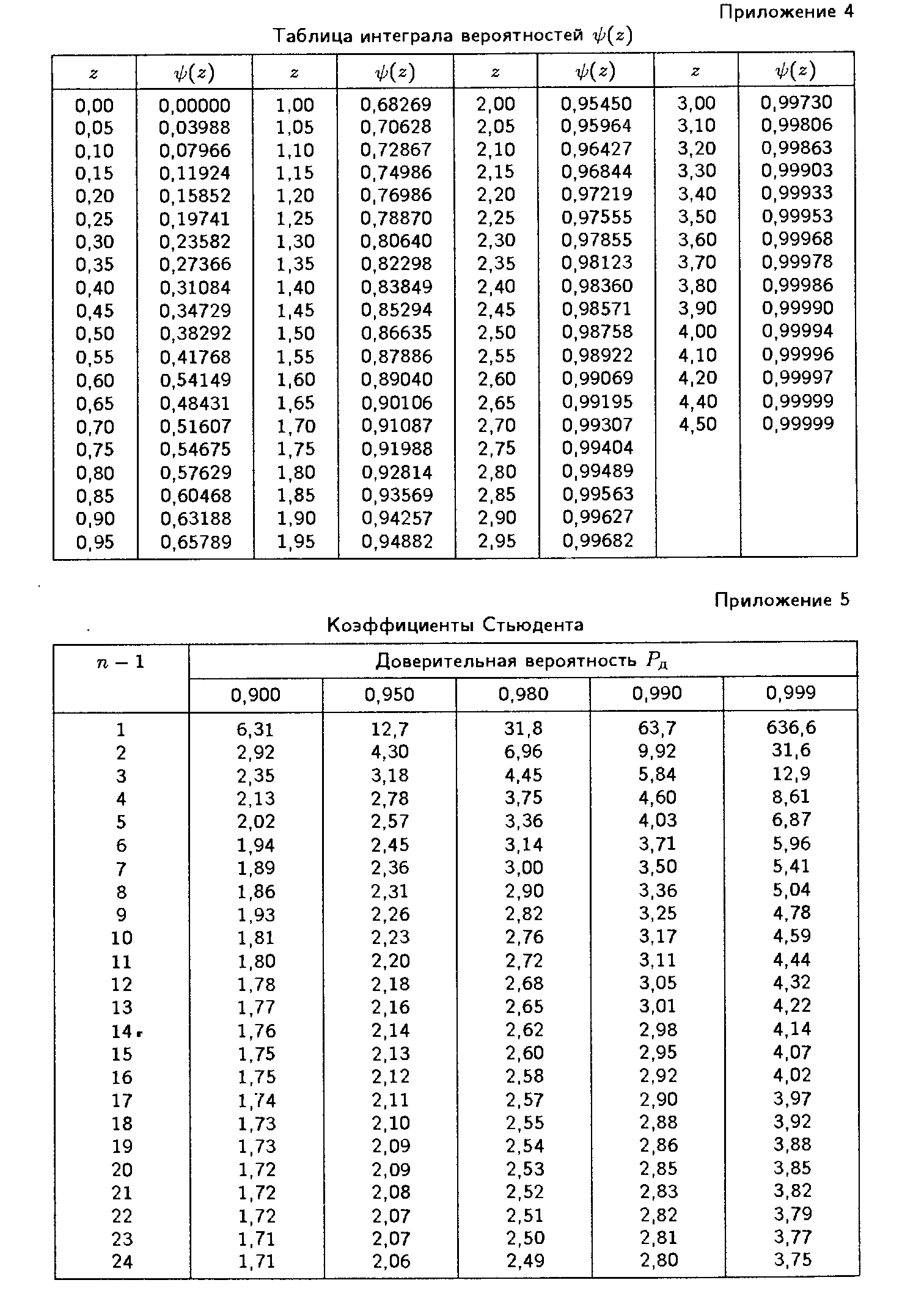
7) находят доверительный интервал по установленной доверительной вероятности, пользуясь интегралом вероятности или плотностью распределения Стьюдента.

Расчеты

Первым делом необходимо определить математическое ожидание заданной величины (среднее арифметическое): по формуле [2]:

где n – количество измерений; - показание i-го измерения.

Подставляем известные данные и получаем:

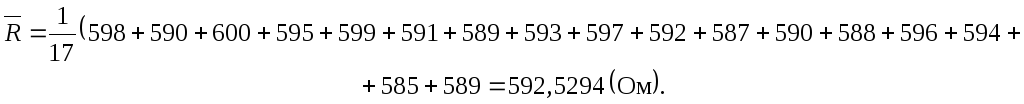
Определим абсолютную погрешность () как разницу между значениями i-го измерения и средним арифметическим ряда из n измерений:

где

Определим абсолютную погрешность первого измерения:

Остальные вычисления производятся аналогично (табл. 1, столбик 5).

Среднеквадратическое отклонение (СКО) погрешности i-го измерения, характеризующее точность измерения:

Определим наличие промахов, используя критерий . Наибольшее по модулю значение абсолютной погрешности, составляет 7,53 Ом

Очевидно, что:

тогда

Можно сделать вывод, что по критерию ряд экспериментально определенных значений не имеет грубых погрешностей.

Точность результата 17 измерений характеризуется оценкой СКО среднего арифметического значения:

Доверительный интервал определим по доверительной вероятности (Р_Д=0,98). При помощи таблицы определим коэффициента Стьюдента

t_cт=2,58

Границы доверительного интервала:

Получаем, величину измеряемого сопротивления с учётом погрешности:

№ измерения	, Ом
1	598	0,98	592,5294	5,47	4,445751	1,078253	2,781893
2	590			-2,53
3	600			7,47
4	595			2,47
5	599			6,47
6	591			-1,53
7	589			-3,53
8	593			0,47
9	597			4,47
10	592			-0,53
11	587			-5,53
12	590			-2,53
13	588			-4,53
14	596			3,47
15	594			1,47
16	585			-7,53
17	589			-3,53

Вывод: В ходе работы была проведена статистическая обработка ряда из 17 измерений. Результаты расчетов были сведены в таблицу. Приобрели навыки расчета погрешностей многократных равноточных измерений, выявления грубых погрешностей методом _.

При обработке заданного ряда экспериментальных данных, установлено, что заданный ряд не имеет грубых погрешностей, величина границ доверительного интервала с вероятностью 0,98 составляет ±2,781893 Ом, математическое ожидание измеряемой величины составляет 592,5294 Ом.

Список литературы:

1. Боридько С.И. Дементьев Н.В. «Метрология и электрорадиоизмерения в телекоммуникационных системах» 2007

2. Кушнир. Ф.В. Электрорадиоизмерения М.: «Энергоатомиздат», 1983 год.

3. Радкевич Я.М., Схиртладзе А.Г., Лактионов Б.И. «Метрология, стандартизация и сертификация», Москва, 2003

4. Ушаков И.Е, «Прикладная метрология. Учебник для вузов» СЗТУ, 2002

Приложение

Лист замечаний

16