
- •Лабораторная работа № 1
- •Методом магнетрона
- •Основные понятия
- •Методика эксперимента
- •Описание экспериментальной установки и порядок выполнения работы
- •Расчёт погрешностей
- •Основные понятия
- •Методика эксперимента.
- •Описание экспериментальной установки и порядок выполнения работы
- •Расчёт погрешностей
- •Изучение вынужденных колебаний в колебательном контуре
- •Основные понятия
- •Методика эксперимента
- •Описание экспериментальной установки и порядок выполнения работы
- •Расчёт погрешностей
- •Лабораторная работа 4 изучение релаксационных колебаний
- •Основные понятия
- •Методика эксперимента
- •Описание экспериментальной установки и порядок выполнения работы
- •Расчёт погрешностей
- •Методика эксперимента
- •Расчёт погрешностей
- •Лабораторная работа 6 изучение свойств ферромагнетиков
- •Основные понятия
- •Методика эксперимента
- •Расчёт погрешностей
- •Коэффициенты Стьюдента cn
- •Саратов 2006
Расчёт погрешностей
1. Систематические погрешности измерения периода «биений» определить по методике вычисления погрешности косвенных измерений [4]:
![]()
где
![]() −
абсолютная погрешность определения
периода колебаний с помощью временной
развёртки осциллографа,
−
абсолютная погрешность определения
периода колебаний с помощью временной
развёртки осциллографа,![]() погрешность
определения числа периодов в одном
биении. Для каждого результата измерений
на графике зависимости п.8 построить
доверительные границы всех результатов
измерений.
погрешность
определения числа периодов в одном
биении. Для каждого результата измерений
на графике зависимости п.8 построить
доверительные границы всех результатов
измерений.
Лабораторная работа 6 изучение свойств ферромагнетиков
Цель работы: изучение свойств ферромагнетиков; исследование динамической петли гистерезиса и кривой намагничивания; определение характеристик ферромагнетика: остаточной индукции, коэрцитивной силы, магнитной проницаемости и потерь энергии на перемагничивание.
Основные понятия
Если
в магнитное поле, образованное токами
в проводах, ввести то или иное вещество,
поле изменится. Это объясняется тем,
что всякое вещество является магнетиком,
т.е. способно под действием магнитного
поля намагничиваться - приобретать
магнитный момент. Намагниченное вещество
создает свое магнитное поле ![]() ,
которое вместе с первичным полем
,
которое вместе с первичным полем ![]() ,
обусловленным токами проводимости,
образует результирующее поле:
,
обусловленным токами проводимости,
образует результирующее поле:
![]() .
(6.1)
.
(6.1)
Эксперименты показывают, что магнетики могут как усиливать, так и ослаблять внешнее поле. Все магнетики делятся по своим магнитным свойствам на три класса: диамагнетики, парамагнетики и ферромагнетики.
Намагничивание пара- и диамагнетиков происходит следующим образом. В настоящее время установлено, что молекулы многих веществ обладают собственным магнитным моментом, обусловленным внутренним движением зарядов. Каждому магнитному моменту соответствует элементарный круговой ток, создающий в окружающем пространстве магнитное поле. Магнитный момент молекулы представляет собой векторную сумму магнитных моментов электронов и ядер. Магнитный момент электрона, вызванный его движением по орбите вокруг ядра, называется орбитальным магнитным моментом. Кроме того, электрон обладает собственным магнитным моментом. Вещества, у которых магнитный момент атомов или молекул не равен нулю в отсутствие внешнего поля, называются парамагнетиками.
Если внешнее магнитное поле отсутствует, то магнитные моменты молекул парамагнетика ориентированы беспорядочно, поэтому обусловленное ими результирующее магнитное поле равно нулю. Равен нулю и суммарный магнитный момент вещества.
Если
же парамагнитное вещество поместить
во внешнее магнитное поле, то под
действием этого поля магнитные моменты
молекул приобретают преимущественную
ориентацию в одном направлении и вещество
намагничивается − его суммарный
магнитный момент становится отличным
от нуля. При этом магнитные поля
отдельных молекул не компенсируют
друг друга, и в результате возникает
поле ![]() .
.
Иначе
происходит намагничивание веществ,
молекулы которых при отсутствии
внешнего поля не имеют магнитного
момента. Если полный магнитный момент
каждой молекулы в отсутствие поля
равен нулю, то вещество, состоящее из
таких молекул, называется диамагнитным.
Внесение таких веществ во внешнее поле
индуцирует элементарные круговые токи
в молекулах, и молекулы, а вместе с
ними и все вещество, приобретают
магнитный момент, направленный в сторону,
противоположную внешнему магнитному
полю. Возникающее внутреннее поле
![]() в диамагнетике ослабляет внешнее
магнитное поле.
в диамагнетике ослабляет внешнее
магнитное поле.
Диамагнетики
и парамагнетики при внесении во внешнее
магнитное поле намагничиваются
слабо. Степень намагничивания магнетика
характеризуется магнитным моментом
единицы объема. Эту величину называют
намагниченностью и обозначают ![]() .
.
По определению
![]() ,
(6.2)
,
(6.2)
где
![]() −
объем магнетика;
−
объем магнетика; ![]() −
магнитный момент отдельной молекулы.
−
магнитный момент отдельной молекулы.
Суммирование
проводится по всем молекулам в объеме
![]() .
.
Магнитное
поле можно характеризовать не только
вектором индукции ![]() ,
но также и вектором напряженности
магнитного поля
,
но также и вектором напряженности
магнитного поля ![]() .
.
Вектор
намагниченности ![]() и вектор напряженности
и вектор напряженности ![]() пропорциональны друг другу:
пропорциональны друг другу:
![]() ,
(6.3)
,
(6.3)
где
![]() –
коэффициент пропорциональности,
называемый магнитной восприимчивостью
вещества. Это безразмерная величина,
характерная для каждого магнетика.
–
коэффициент пропорциональности,
называемый магнитной восприимчивостью
вещества. Это безразмерная величина,
характерная для каждого магнетика.
Магнетики,
подчиняющиеся зависимости (6.3), подразделяют
на парамагнетики ![]() и диамагнетики
и диамагнетики![]() .
У парамагнетиков
.
У парамагнетиков ![]() ,
у диамагнетиков
,
у диамагнетиков![]() .
.
По
определению векторы ![]() и
и ![]() связаны
соотношением:
связаны
соотношением:
![]() ,
.(6.4)
,
.(6.4)
где
![]() ;
;
![]() −
магнитная постоянная, равная l,26∙10-6
Гн/м.
−
магнитная постоянная, равная l,26∙10-6
Гн/м.
Подставляя (6.3) в (6.4), получим:
![]() ,
,
Откуда
![]() ,
(6.5)
,
(6.5)
где
![]() ––магнитная
проницаемость среды и, следовательно,
––магнитная
проницаемость среды и, следовательно,
![]() .
( 6.6)
.
( 6.6)
У
парамагнетиков ![]() ,
у диамагнетиков
,
у диамагнетиков ![]() ,
причем, как у тех, так и у других, магнитная
проницаемость отличается от единицы
весьма мало, т.е. магнитные свойства
этих магнетиков выражены очень слабо.
,
причем, как у тех, так и у других, магнитная
проницаемость отличается от единицы
весьма мало, т.е. магнитные свойства
этих магнетиков выражены очень слабо.
Ферромагнетики. Ферромагнитными называют вещества, которые могут обладать спонтанной намагниченностью, т.е. могут быть уже намагничены при отсутствии внешнего магнитного поля.
Характерной
особенностью ферромагнетиков является
нелинейная зависимость ![]() или
или ![]() (рис. 6.1 и 6.2).
(рис. 6.1 и 6.2).
На
рис. 6.1 приведена кривая намагничения
ферромагнетика, намагниченность
которого при ![]() =0
также равна нулю, ее называют основной
кривой намагничения. Уже при сравнительно
небольших значениях
=0
также равна нулю, ее называют основной
кривой намагничения. Уже при сравнительно
небольших значениях ![]() намагниченность
намагниченность ![]() достигает насыщения
достигает насыщения ![]() ,
магнитная индукция
,
магнитная индукция ![]() также растет с увеличением
также растет с увеличением![]() .
После достижения состояния насыщения
.
После достижения состояния насыщения
![]() продолжает расти с увеличением
продолжает расти с увеличением ![]() по
линейному закону
по
линейному закону ![]() ,
где
,
где ![]() .
.
J B
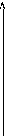

![]()





Н
Н

Рис. 6.1. Зависимость![]() Рис. 6.2. Зависимость
Рис. 6.2. Зависимость![]()
На
рис. 6.2 приведена основная кривая
намагничивания на диаграмме зависимости
![]() от
от ![]() .
Вследвие нелинейной зависимости
.
Вследвие нелинейной зависимости ![]() для ферромагнетиков
нельзя ввести магнитную проницаемость
для ферромагнетиков
нельзя ввести магнитную проницаемость
![]() как определенную постоянную величину,
характеризующую магнитные свойства
каждого данного ферромагнетика.
Однако по-прежнему считают, что
как определенную постоянную величину,
характеризующую магнитные свойства
каждого данного ферромагнетика.
Однако по-прежнему считают, что ![]() при этом является функцией
при этом является функцией ![]() .
Магнитная проницаемость
.
Магнитная проницаемость ![]() для ферромагнетиков может достигать
очень больших значений. Так, например,
для чистого железа магнитная проницаемость
равна 6000, для сплава суперпермаллой —
800000. Заметим, что понятие магнитной
проницаемости применяется только к
основной кривой намагничивания, т.к.
зависимость
для ферромагнетиков может достигать
очень больших значений. Так, например,
для чистого железа магнитная проницаемость
равна 6000, для сплава суперпермаллой —
800000. Заметим, что понятие магнитной
проницаемости применяется только к
основной кривой намагничивания, т.к.
зависимость![]() неоднозначна.
Рассмотрим эту зависимость. Кроме
нелинейной зависимости
неоднозначна.
Рассмотрим эту зависимость. Кроме
нелинейной зависимости ![]() или
или ![]() для ферромагнетиков характерно также
явление магнитного гистерезиса (рис.
6.3).
для ферромагнетиков характерно также
явление магнитного гистерезиса (рис.
6.3).
![]() и
и ![]() оказывается неоднозначной и определяется
предшествующей историей намагничивания
ферромагнетика. Если первоначально
ненамагниченный ферромагнетик
намагничивать, увеличивая
оказывается неоднозначной и определяется
предшествующей историей намагничивания
ферромагнетика. Если первоначально
ненамагниченный ферромагнетик
намагничивать, увеличивая ![]() от нуля до значения, при котором наступает
насыщение (точка 1 на рис. 6.З), а затем
уменьшать
от нуля до значения, при котором наступает
насыщение (точка 1 на рис. 6.З), а затем
уменьшать ![]() от
от ![]() до -
до -![]() ,
то кривая намагничения
,
то кривая намагничения ![]() пойдет не по первоначальному пути
10, а выше – по пути 1234. Если дальше
изменять
пойдет не по первоначальному пути
10, а выше – по пути 1234. Если дальше
изменять ![]() в обратном направлении от
в обратном направлении от ![]() до
до ![]() ,
то кривая намагничения пройдет ниже —
по пути 4561. Получившуюся замкнутую
кривую называют петлей гистерезиса.
В том случае, когда в точках 1 и 4
достигается насыщение, получается
максимальная петля гистерезиса.
Когда же в крайних точках 1 и 4 насыщения
нет, получатся аналогичные петли
гистерезиса, но меньшего размера, как
бы вписанные в максимальную петлю.
,
то кривая намагничения пройдет ниже —
по пути 4561. Получившуюся замкнутую
кривую называют петлей гистерезиса.
В том случае, когда в точках 1 и 4
достигается насыщение, получается
максимальная петля гистерезиса.
Когда же в крайних точках 1 и 4 насыщения
нет, получатся аналогичные петли
гистерезиса, но меньшего размера, как
бы вписанные в максимальную петлю.
H
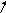
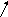
Рис. 6.3. Петля гистерезиса
Из
рис. 6.3 видно, что при
![]() =0
намагничивание не исчезает и характеризуется
величиной
=0
намагничивание не исчезает и характеризуется
величиной ![]() ,называемой
остаточной индукцией. Ей соответствует
остаточная намагниченность
,называемой
остаточной индукцией. Ей соответствует
остаточная намагниченность![]() .
С наличием такого остаточного
намагничивания связано существование
постоянных магнитов. Величина
.
С наличием такого остаточного
намагничивания связано существование
постоянных магнитов. Величина ![]() обращается в ноль
обращается в ноль
![]() ,
имеющего направление, противоположное
полю, вызвавшему намагничивание.
Величина
,
имеющего направление, противоположное
полю, вызвавшему намагничивание.
Величина ![]() называется коэрцитивной силой.
Значения
называется коэрцитивной силой.
Значения ![]() для разных ферромагнетиков меняются
в широких пределах.
для разных ферромагнетиков меняются
в широких пределах.
При повышении температуры способность ферромагнетиков намагничиваться уменьшается, в частности, уменьшается намагниченность насыщения. При некоторой температуре, называемой температурой или точкой Кюри, ферромагнитные свойства исчезают. При температурах, более высоких, чем температура Кюри, ферромагнетик превращается в парамагнетик.
Физическую природу ферромагнетизма удалось понять только с помощью квантовой механики. При определенных условиях в кристаллах могут возникать так называемые обменные силы, которые заставляют магнитные моменты электронов устанавливаться параллельно друг другу. В результате возникают области размером (1 – 10) мкм спонтанного, т.е. самопроизвольного намагничивания. Эти области называются доменами. В пределах каждого домена ферромагнетик намагничен до насыщения и имеет определенный магнитный момент. Направления этих моментов для различных доменов различны, поэтому при отсутствии внешнего поля суммарный момент образца равен нулю и образец в целом представляется макроскопически не намагниченным.
При включении внешнего магнитного поля домены, ориентированные по полю, растут за счет доменов, ориентированных против поля. Такой рост доменов в слабых полях имеет обратимый характер. В более сильных полях происходит одновременная переориентация магнитных доменов в пределах всего объема вещества. Этот процесс является необратимым, что служит причиной гистерезиса и остаточного намагничивания.
Сказанное выше может быть пояснено с помощью следующей схемы (рис. 6.4).
![]()

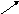

![]()
![]()
![]()












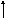
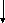
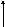

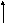


![]()





а б в г
Рис. 6.4. Процесс намагничивания ферромагнитного материала
Процесс
намагничивания рассмотрим на примере
кубика, выполненного из ферромагнитного
материала, который помещен в магнитное
поле индукции ![]() ,
параллельное одной из его
диагональных плоскостей
,
параллельное одной из его
диагональных плоскостей
(рис. 6.4,а). При увеличении поля энергетически выгодные домены, у которых вектор намагничивания составляет с направлением поля острый угол, растут за счет энергетически невыгодных доменов, причем эти изменения обратимы в слабых полях (рис. 6.4,б). Далее происходят процессы необратимого изменения границ (рис. 6.4,в). После того, как все энергетически невыгодные домены исчезнут, векторы намагниченности доменов поворачиваются параллельно внешнему полю – ориентационное намагничивание. Этот «процесс поворота» заканчивается, когда весь кристалл равномерно намагнитится, т.е. наступает насыщение (рис. 6.4,г).
