Методика эксперимента

Рассмотрим случай слабой связи между контурами, т.е. предположим, что С₁₂>>С. Тогда частоты нормальных колебаний ω₁ и ω₂ близки друг к другу и можно положить, что ω₁ ≈ ω₂ , (ω₁ + ω₂)=2 ω₁ ,а (ω₁ - ω₂)=Δω, где Δω << ω₁ . Тогда соотношения (5.8) и (5.9) можно переписать в виде:

, (5.10)

, (5.11)

Получившиеся выражения (5.10) и (5.11) есть произведения двух колебаний. Вторые множители в них представляют собой быстро меняющиеся гармонические функции с частотой, близкой к частоте ω₁≈ ω₂, первые же множители обладают, в силу условия близости частот ω₁и ω₂, малой частотой, т.е. большим периодом. Это позволяет рассматривать колебания зарядовq₁иq₂как почти гармонические с частотами ω₁и медленно меняющимися амплитудамиисоответственно. Подобные колебания изображены на рис. 5.3 и 5.4. Пунктирные линии представляют графики медленно меняющихся амплитуд. Сплошной линией на тех же рисунках представлены графики результирующих колебаний (5.10) и (5.11). Такое постепенное возрастание и убывание амплитуды носит название биений. Следует обратить внимание на то, что приt=0 амплитуда колебаний заряда на втором конденсаторе А₂равна нулю. Амплитуда А₂увеличивается, а амплитуда А₁падает до тех пор, пока в момент времени, определённый из соотношения, амплитуда А₁не станет равной нулю, а амплитуда А₂достигнет максимума.

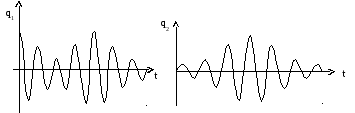
Рис. 5.3. Зависимость Рис.5.4. Зависимость

Ситуацию, показанную на рис. 5.3 и 5.4, можно рассмотреть с энергетической точки зрения.

При t=0 вся энергия сосредоточена в контуре 1. В результате связи через ёмкость С₁₂ энергия постоянно передаётся от контура 1 к контуру 2 до тех пор, пока вся энергия не соберется в контуре 2. Время, необходимое для перехода энергии из контура 1 в контур 2 и обратно, можно получить из уравнения :

, (5.12)

а частота, с которой контуры обмениваются энергией:

. (5.13)

Для моды нормальных колебаний с частотой ω₁ токи текут в одинаковом направлении, тогда на емкости С₁₂ нет заряда. При этом частота ω₁ остаётся такой же, как для несвязанных контуров ω₁==ω₀. В случае моды нормальных колебаний с частотой ω₂ емкость заряжена, что увеличивает частоту колебаний .

В случае слабой связи выражение (5.13) можно преобразовать следующим образом:

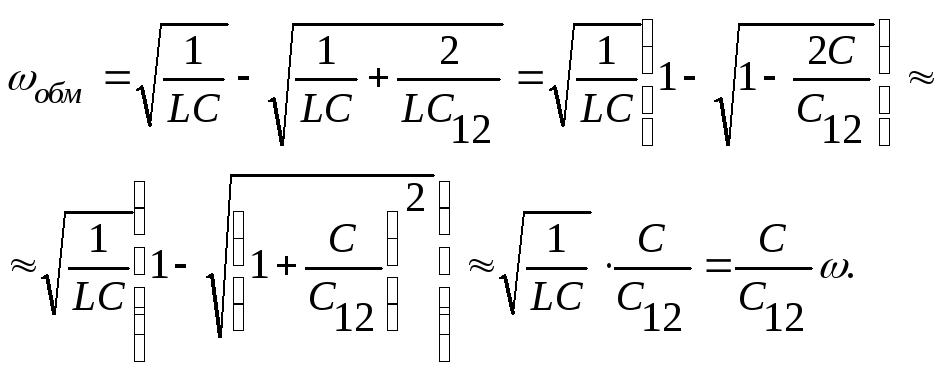(5.14)

Полученное значение частоты обмена энергией или частоты биений можно изменять, настраивая систему контуров, меняя параметры контуров С, С₁₂ и L. Период биений равен :

. (5.15)

Исследование биений, т.е. обмена энергией в связанных контурах, и является одной из практических задач данной работы.

Мы рассмотрели работу схемы (рис. 5.2), предполагая, что омическое сопротивление в контурах отсутствует. В любом реальном контуре его сопротивление R отлично от нуля. Поэтому возникающие в связанных контурах колебания будут со временем затухать, т.е. амплитуды А₁ и А₂ со временем будут уменьшаться. На рис. 5.5 представлен график, определяющий реально существующие в контурах биения.

N=3

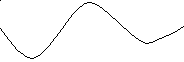
t

Рис. 5.5.Биения в реальных связанных контурах

Описание экспериментальной установки и порядок выполнения работы

Электрическая схема установки представлена на рис.5.6 и содержит: источник питания ИП, преобразователь импульсов ПИ, звуковой генератор PQ,осциллограф РО, магазин емкостей МЕ, модуль ФПЭ-13.

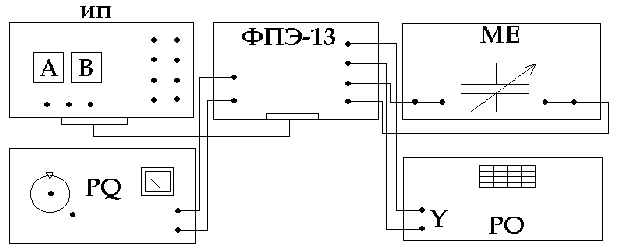
Рис. 5.6. Блок-схема экспериментальной установки

Задание 1. Определение периода биений.

1. Собрать схему (рис. 5.6), установить с помощью магазина емкостей (МЕ) емкость С =4·10^-2мкФ.

2. Включить звуковой генератор. Установить следующие параметры выходного напряжения звукового генератора: частота 200 Гц, величина выходного напряжения 2-4 В, режим работы – генерация синусоидальных колебаний.

3. Включить развертку электронного осциллографа в режиме «Внутренняя синхронизация» и установить частоту развертки, удобную для наблюдения сигналов частотой 200 Гц.

4. Включить лабораторный стенд и приборы. Регулировкой ручек управления на панели осциллографа добиться стабильной картины процесса «биений» в контурах.

5. Изменяя величину емкости конденсатора связи С₁₂ на магазине емкостей от 4·10^-2 до 4·10^-1мкФ, измерить количество периодов, т.е. количество максимумов, укладывающихся в одно «биение» N (рис. 5.5). Полученные значения записать в таблицу.

6. Вычислить период собственных колебаний свободного колебательного контура по формуле Томпсона Т₀=2π.

7. По полученным значением Т₀ и числу периодов N, укладывающихся в одно «биение» N рассчитать частоту биений Т_б = Т_оN. Рассчитанные значения записать в таблицу.

8. По полученным таким образом значениям Т_б построить график зависимости Т_б =ƒ (С₁₂).

9. Провести расчеты периода Т_б по (15) и сравнить их с экспериментальными значениями.