Результант
.docЛекция № 23
Результант
Результантом полиномов
и
,
имеющих степени n>0 и m>0 называют следующий определитель порядка (n+m):
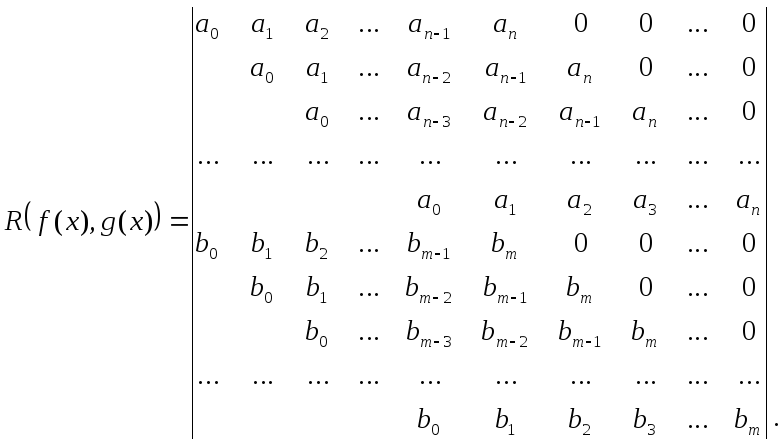(1)
Например,
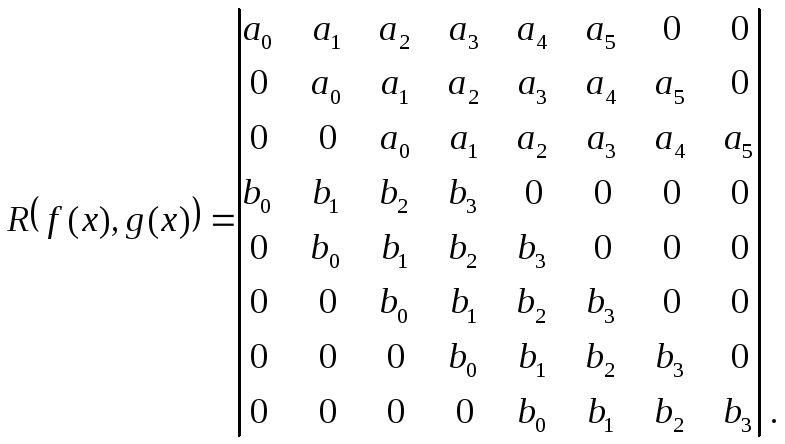
Здесь определитель записан при n=5, m=3. Определитель (1) записан для случая, когда n=m.
Теорема.
Полиномы
,
имеют общий корень тогда и только тогда, когда их результант равен 0: R(f(x),g(x))=0.
Пример 1.
Для полиномов
и
их результантом является определитель 6-го порядка
.
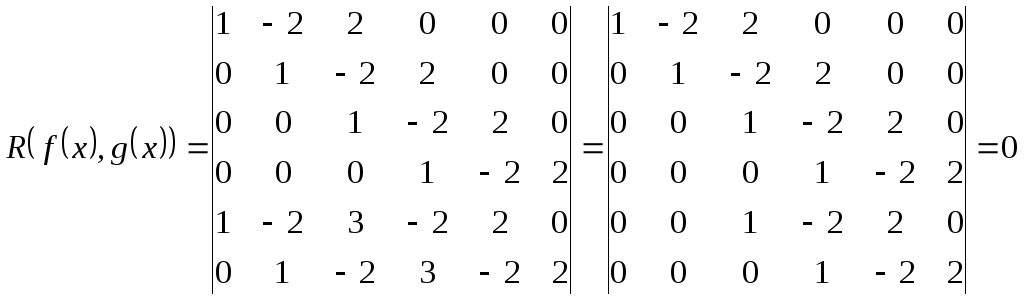Во втором определителе третья и пятая строки одинаковы.
Пример 2.
Вычислить, при
каких значениях
полиномы
и
имеют общие корни.
Решение.
Вычисляем результант:
.
f(x)
и g(x)
имеют общие корни лишь в случае, когда
0,
то есть при λ=±1. При λ=1 общими корнями
являются i
и –i,
а при λ= –1:
1 и –1.
Пример для самостоятельного решения.
Вычислить результант
многочленов
и
.
Дискриминант многочлена
Определение.
Дискриминантом многочлена
,
имеющего корнями
числа
,
называется произведение
.
Дискриминант тогда и только тогда равен нулю, когда среди корней многочлена имеются равные, то есть когда многочлен имеет хотя бы один кратный корень. Дискриминант связан с результантом многочлена f(x) и его производной f'(x) равенством
,
позволяющей выразить дискриминант через его коэффициенты.
Пример 3.
Найти дискриминант многочлена
.
Решение.
.
.
,
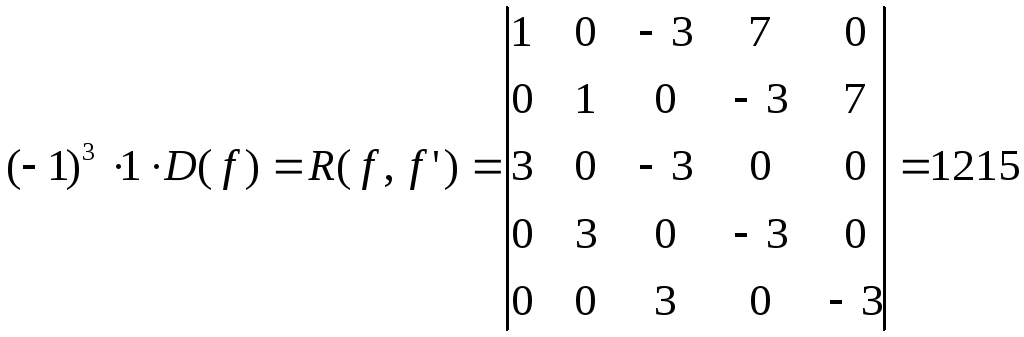f(x)
кратных корней не имеет.
Пример для самостоятельного решения
Найти дискриминант многочлена
.
Можно выразить
через коэффициенты многочлена
и другим путем, пользуясь тем, что
является симметрическим многочленом
от корней
.
Формулы Виета
Корни
многочлена
связаны с его коэффициентами по формулам Виета:
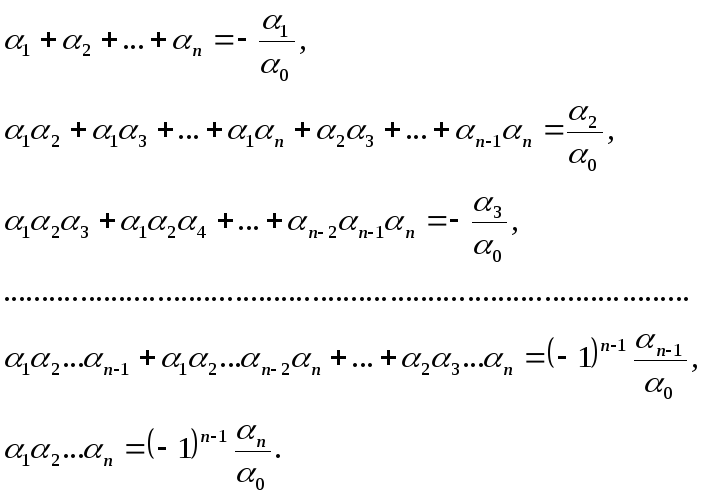
Элементарные симметрические многочлены от n переменных:
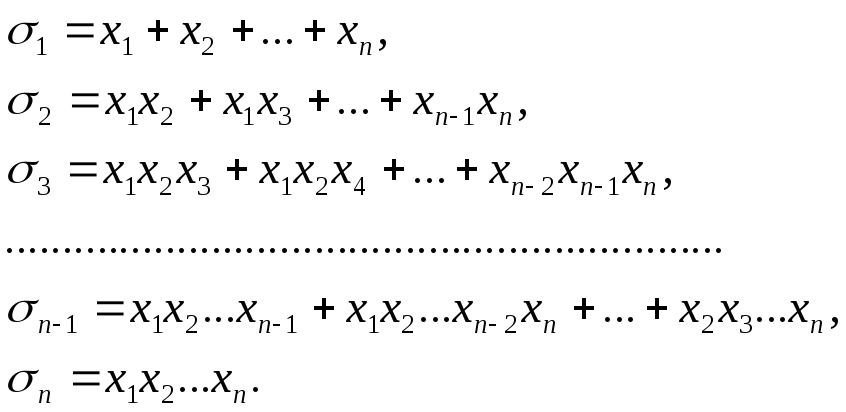
Степенными суммами называются симметрические многочлены
С элементарными симметрическими многочленами они связаны формулами Ньютона:
при
;
при
.
Из этих формул
можно находить
через
или наоборот.
,
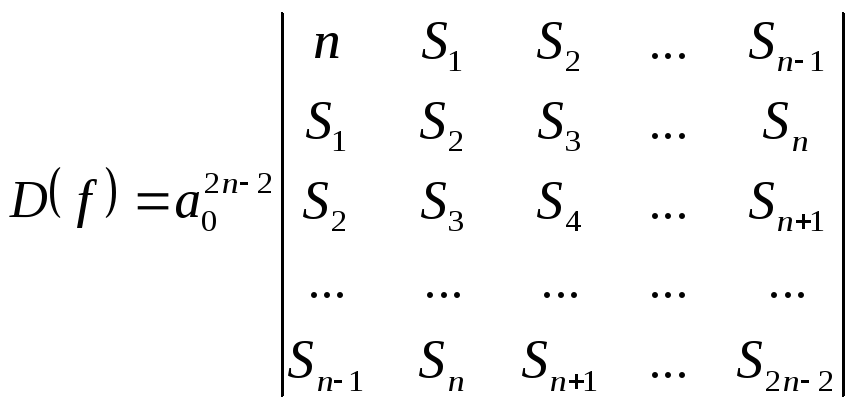где
- сумма i-х степеней корней
многочлена
.
Пример.
Найти дискриминант
многочлена
.
Решение.
,
,
.
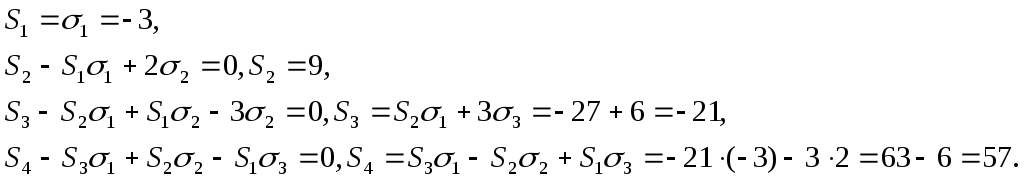
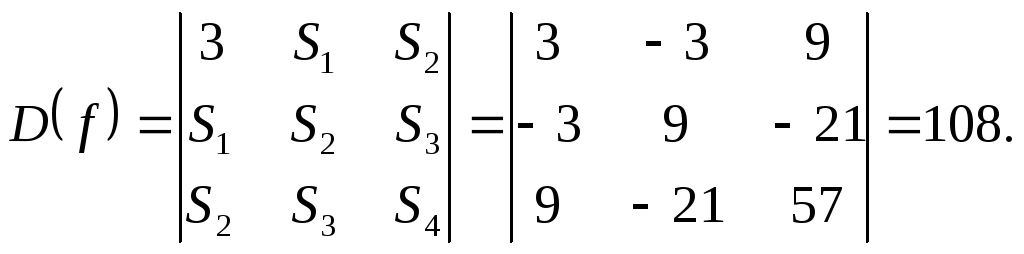
Ответ:
Примеры для самостоятельного решения:
а) найти дискриминант
многочлена
б)
