7.4. Основное уравнение молекулярно-кинетической теории идеального газа.

Основное уравнение молекулярно-кинетической теории идеального газа связывает макроскопический параметр газа с микроскопическими характеристиками, относящимися к его структурным элементам - молекулам. Учитывая беспорядочное непрерывное движение молекул и их соударения со стенками сосуда и друг с другом, макроскопическим параметром может быть давление газа, которое связано с изменением импульса молекул (микроскопический параметр).

Как известно, величина давления определяется силой, действующей перпендикулярно на единицу площади поверхности: .

Рис. 7.5

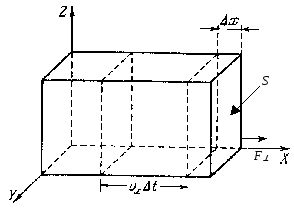
Давление газа на стенки обусловлено огромным числом столкновений молекул газа со стенками, согласно второму закону Ньютона :

Импульс одной молекулы: вдоль оси Х равен , гдеm₀ - масса одной молекулы. Пусть в единице объема сосуда находится n молекул, из них половина движется вдоль оси Х, а другая половина - в противоположном направлении. За время Dt в слой Dx (Dx – расстояние, на котором проявляется действие молекул на стенку) слева направо входит молекул. Каждая из них обладает импульсом, следовательно, общий импульс, вносимый ими в слой, равен:.

За это же время слой покидает, двигаясь, справа налево, такое же число молекул с таким же общим импульсом, но противоположного знака. Общее изменение импульса: .

Импульс силы, действующей на стенку, площадью S, равен изменению импульса частиц . Тогда давление на стенку, будет определяться формулой:

(7-7)

Двигаясь беспорядочно в пространстве, молекулы имеют составляющие скоростей и вдоль других осей. Полная скорость молекулы может быть выражена через её составляющие по трём независимым направлениям : .

Поскольку в движении участвует множество молекул, то необходимо использовать средние квадраты скоростей:.

Так как движение беспорядочное, то все три компоненты скоростей равноправны. Отсюда . После подстановки в уравнение (7-7) получим:(7-8)

Уравнение (7-8) связывает макроскопический параметр давление и микроскопические – массу и средний квадрат скорости молекулы, поэтому его можно считать основным уравнением МКТ идеальных газов. Однако, часто это уравнение используют в другом виде: . Здесь- средняя кинетическая энергия поступательного движения молекулы. Таким образом, давление идеального газа определяется средней кинетической энергией поступательного движения молекулы и является среднестатистической величиной

(7-9)

Давление газа пропорционально средней кинетической энергии поступательного движения молекулы.

Единица давления в СИ: 1 Па =1 Н/м²

7.5. Закон Максвелла для распределения молекул по скоростям.

Распределение большого числа молекул идеального газа, находящегося в состоянии термодинамического равновесия, по модулям скоростей подчиняется закону распределения Максвелла. Для получения дифференциального распределения Максвелла будем искать число частиц, скорости которых лежат в очень малом интервале dвблизи некоторой скорости . Пусть dn – число частиц в единице объёма, скорости которых лежат в интервале от до dЭто число пропорционально интервалу скоростей d, а также пропорционально числу частиц в единице объёма. Можно записать так:

, (7-10)

где - плотность вероятности скорости, которая означает долю частиц в единице объёма, скорости которых лежат в единичном интервале скоростей вблизи скорости Тогда доля частиц, скорости которых лежат в интервале от до  dможет быть найдена как

(7-11)

Поскольку число частиц, даже в малых объёмах вещества, очень велико, то имеет смысл вероятности того, что любая частица идеального газа в единице объёма имеет скорость, лежащую в интервале скоростей от до dРаспределение Максвелла в дифференциальной форме имеет вид:

(7-12)

Вид дифференциального распределения Максвелла при разных значениях температуры представлен на рис.7.6. Площадь заштрихованной криволинейной трапеции численно равна доле частиц, скорости которых лежат в интервале от до  dСкорость , соответствующая максимуму плотности вероятности, называетсянаиболее вероятной скоростью. При выполняется равенство. Отсюда получаем, что наиболее вероятная скорость равна:

или (7-13)

В отличие от распределения Гаусса, распределение Максвелла не симметрично относительно абсциссы максимума функции распределения. Это обусловлено наличием в формуле (7-12) квадрата модуля скорости, кроме экспоненты. При малых скоростях преобладает вклад, поэтому при этих скоростях вид кривой дифференциального распределения (рис.7-6) близок к параболе, приосновной вклад вносит экспонента, которая убывает гораздо быстрее, чем растёт парабола. Площадь фигуры под кривой () на рис.7.6 равна единице (условие нормировки) и выражает факт существования молекулы. При возрастании температуры увеличивается наиболее вероятная скорость, а плотность вероятности, соответствующая этой скорости, уменьшается, но площадь фигуры под кривой остаётся неизменной. Интегральное распределение Максвелла показано на рисунке 7.7. ЗдесьN₁/N – доля частиц, скорости которых превышают скорость.

Таким образом, распределение Максвелла – это равновесное распределение идеального газа. Оно устанавливается благодаря столкновениям молекул, которые приводят систему к тепловому равновесию.

Распределение Максвелла позволяет определить несколько средних скоростей: наиболее вероятную скорость, среднюю арифметическую скорость и среднюю квадратичную скорость.

Скорость , соответствующая максимуму плотности вероятности, называютнаиболее вероятной скоростью. Для идеального газа, находящегося в состоянии термодинамического равновесия при температуре Т, она определяется из условия и равнаили.

Средняя квадратичная скорость определяется как квадратный корень из среднего квадрата скорости и связана со средней кинетической энергией поступательного движения молекул. Чтобы найти её с помощью распределения Максвелла, нужно определить отношение суммы квадратов скоростей молекул, содержащихся в единице объёма, к числу молекул в этом объёме:.

Для идеального газа, находящегося в состоянии термодинамического равновесия при температуре Т, она равна

или (7-14)

Среднюю арифметическую скорость определяют как отношение суммы всех скоростей всех молекул в единице объёма к числу молекул в единице объёма:.

Для идеального газа, находящегося в состоянии термодинамического равновесия при температуре Т , она равна :

. . (7-15)

Эти скорости мало отличаются друг от друга по своим численным значениям : .

Экспериментально равновесное распределение частиц по скоростям было обнаружено Штерном, Истерманом и Симпсоном в 1947 году.