Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технологический университет "Станкин"

Предмет:

Аналитическая геометрия

Файл:

Методичка по аналитической геометрии

.pdf

Скачиваний:

373

Добавлен:

11.02.2015

Размер:

1.93 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

Данные прямые параллельны тогда и только тогда, когда их направляющие векторы a1 (l1, m1, n1 ) и a2 (l2 , m2 , n2 ) коллинеарны (рис.

28, а).

Отсюда

l1	m1	n1
l2	m2	n2	(5.9)
l2	m2	n2

- условие параллельности двух прямых в пространстве.

L1	L2	L2
a1	a2	a2

a1 L1

а)

б)

Рис. 28

Данные прямые перпендикулярны тогда и только тогда, когда их направляющие векторы перпендикулярны (в пространстве перпендикулярные прямые могут быть и не пересекающимися) (рис.

28б).

Отсюда
l1 l2 m1 m2 n1 n2 0	(5.10)

- условие перпендикулярности двух прямых.

За угол между прямыми принимается угол между их направляющими векторами a1 (l1, m1, n1 ) и a2 (l2 , m2 , n2 ) , следовательно,


cos		l1 l2 m1 m2 n1 n2					.
								(5.11)

2		2	2	2	2	2
	l1	m1	n1	l2	m2	n2

a1 M1

		M 2	L2
		a2
		Рис. 29
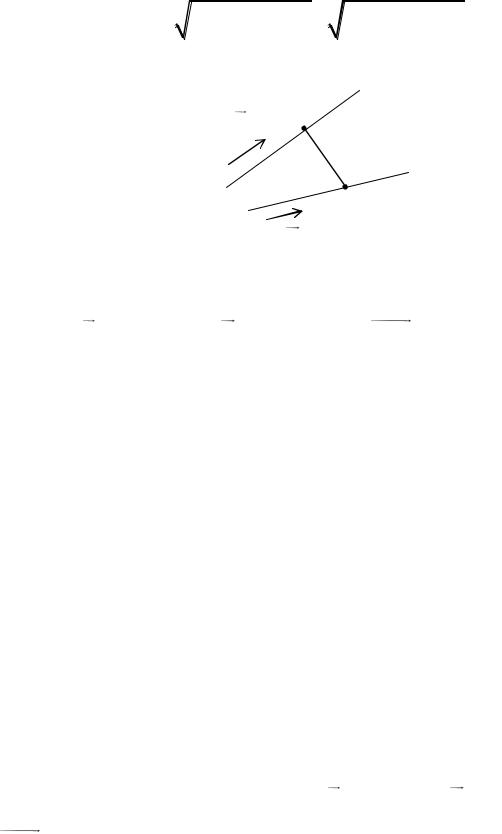
Прямые L1	и L2 являются скрещивающимися тогда и только тогда, когда
векторы	a1 (l1, m1, n1 ) ,	a2 (l2 , m2 , n2 ) и	M1M2 (x2 x1,	y2 y1 , z2 z1 )

некомпланарны (рис. 29). В этом случае их смешанное произведение отлично от нуля, т.е.

l1	m1	n1
l2	m2	n2	0
x2 x1	y2 y1	z2 z1

В противном случае прямые лежат в одной плоскости.

Пример.

Исследовать взаимное расположение двух прямых

L :		x 1		y 2			z 3		;
L :									;
1	9		8					7
	9		8					7
L :		x 6			y 5			z 4		.
L :										.
2		2	3			1
		2	3			1
Решение:
Из уравнений прямых следует, что M1 (1, 2, 3) L1												и	M2 (6, 5, 4) L2 .
Направляющие векторы данных прямых a1 (9, 8,											7)	и a2	( 2, 3, 1) .

M1M2 (6 1, 5 2, 4 3) (5, 3, 1) .

Составим определитель:

9	8	7
9	8	7
2	3	1	203 0 , значит, прямые скрещиваются.
5	3	1

Ответ: прямые скрещиваются.

Решение задач.

1.Составить уравнения прямой, проходящей через точку P(2, 5,3)

а) параллельно оси Oy ;

б) параллельно прямой	x 1		y 3	z 2	;
	4		6	2

в) параллельно прямой x 1,		y 2 3t, z 4t .

Решение:

а) искомая прямая параллельна оси Oy . Значит, в качестве направляющего вектора прямой можно взять любой вектор, лежащий на оси Oy , например, вектор j (0,1, 0) .

Имеем	точку P(2, 5,3) , принадлежащую этой прямой, т.е.
x0 2, y0	5, z0 3, и направляющий вектор этой прямой a j (0,1, 0) , т.е.

l 0, m 1, n 0 .

Составим канонические уравнения прямой, используя (5.1)

x x0

y y0

z z0

В нашем случае:

x 2

y 5

z 3

- уравнения искомой прямой;

б) если прямые параллельны, то их направляющие векторы коллинеарны, в частности, совпадают. Искомая прямая параллельна прямой

x 1	y 3	z 2	, значит, за направляющий вектор можно взять
4	6	2

a (4, 6, 2) .

Точка P(2, 5,3) принадлежит этой прямой, т.е. x0 2, y0 5, z0 3, направляющий вектор этой прямой a (4, 6, 2) , т.е. l 4, m 6, n 2 .

Составим канонические уравнения прямой, используя (5.1)

x x0

y y0

z z0

В нашем случае:

x 2

y 5

z 3

- уравнения искомой прямой;

в) прямая

x 1,

y 2 3t,

z 4t задана параметрическими уравнениями.

Как известно, коэффициенты при t есть координаты направляющего вектора этой прямой, т.е. a1 (0,3, 4) . По условию эта прямая параллельна

искомой прямой, значит,

за направляющий вектор a

нашей прямой мы

можем взять направляющий вектор a1 , т.е. a (0,3, 4) .

Составим канонические уравнения прямой, используя (5.1)

x x0

y y0

z z0

x 2

y 5

z 3

- уравнения искомой прямой.

Ответ: а)

x 2

y 5

z 3

;

б)

x 2

y 5

z 3

;

в)

x 2

y 5

z 3

2. Составить уравнения прямой, проходящей

через вершину B

треугольника

ABC

параллельно

стороне

AC ,

если

A( 1, 1, 2),

B( 2,5, 4), C( 1, 2,1)

Решение:

Вектор AC , расположенный на прямой AC , является для искомой прямой направляющим вектором. Найдем его координаты.

AC (xC xA , yC yA , zC zA ) (1 (1), 2 (1), 1 2) (0, 3, 1) , т.е.

за направляющий вектор прямой примем вектор a (0, 3, 1) .

Точка B(2,5, 4) лежит на прямой, т.е.	x0 2, y0 5, z0 4 ,
направляющий вектор этой прямой a (0, 3, 1) , т.е.	l 0, m 3, n 1.

Пользуясь формулой (5.1), составим канонические уравнения прямой:

x x0

y y0

z z0

В нашем случае:

x 2

y 5

z 4

- уравнения искомой прямой.

Ответ:

x 2

y 5

z 4

3.Составить уравнение медианы треугольника ABC , проведенной

из вершины C , если A(1, 1, 2), B(2, 2, 4), C(3,5,1) .

Решение:

По условию CD - медиана треугольника ABC (рис. 30).

A C

Рис. 30

Следовательно, D - середина отрезка AB . Найдем координаты середины отрезка по формулам (1.3):

x	xA xB	, y			yA yB	, z			zA zB	;
	2
D			D	2			D	2

x	12	3, y	D		12	1	, z	D		24	1;

D	2	2		2		2			2

D( 32 , 12 , 1) .

Для составления уравнения медианы воспользуемся уравнениями (5.2) прямой, проходящей через две точки

x x0					y y0			z z0		, где
x x					y y					, где
x x					y y			z z	0
1		0			1	0	1		0
C(3,5,1) принадлежит прямой, т.е.											x0 3, y0 5, z0				1;
D(	3	,	1	, 1) также принадлежит прямой, т.е.								x	3	,	y	1	, z 1:
D(		,		, 1) также принадлежит прямой, т.е.								x		,	y		, z 1:
2		2										1	2		1	2	1
2		2											2			2

x 3			y 5			z 1
3	3		1	5		11
3			1			11
2			2
x 3		y 5			z 1

	9			9		2
	2			2

;

или	x 3	y 5	z 1	- уравнения искомой прямой.
	9	9	4

Ответ:							x 3						y 5		z 1	.
Ответ:														9		.
							9							9	4
		7.			Составить уравнения прямой, проходящей через точку P(2, 1,3) и
					точку пересечения прямой													x 2		y		z 1	с плоскостью		XY .
					точку пересечения прямой																		с плоскостью		XY .
																	2		3		2
Решение:
Найдем точку пересечения																	P данной прямой с плоскостью								XY . Точки,
																	1
лежащие в плоскости XY ,																	имеют координаты (x , y , 0) . Если точка P
																					0			0	1
принадлежит прямой, то ее координаты удовлетворяют уравнению:
	x0 2					y0			0 1					, отсюда
		2						2						, отсюда
		2				3		2
	x0		2			1	,			x0 3 ;
		2				2	,			x0 3 ;
		2				2
	y0			1	,		y				3	.
					,		y					.
3		2					0	2
3		2						2
																	65

Т.е. точка

P (3,

, 0)

точка пересечения данной прямой с плоскостью

XY .

Составим

уравнения

искомой

прямой,

проходящей через две точки

P(2, 1,3) и P (3,

, 0) , для этого воспользуемся уравнениями (5.2):

x x0

y y0

z z0

;

x x

y y

z z

x 2

y 1

z 3

;

3 2

0 3

x 2

y 1

z 3

или

x 2

y 1

z 3

- уравнения искомой прямой.

Ответ:

x 2

y 1

z 3

Точка

M симметрична

точке

N(3, 2,1)

относительно плоскости

XZ . Составить уравнение плоскости, проходящей через точку M ,

перпендикулярно прямой x 1 y z 2 .

Решение:

Поскольку

точка

симметрична

точке

N(3, 2,1) относительно

плоскости

XZ , то координата

y изменит знак, координаты x и z не

изменятся (рис. 31)

	z
N	M
y1	y y

Рис. 31

Значит, M (3, 2,1) .
Искомая	плоскость	перпендикулярна	прямой	x 1 y z 2 ,

следовательно, в качестве нормального вектора плоскости можно взять

направляющий	вектор прямой.	Прямая задана каноническими
уравнениями,	направляющий вектор	этой прямой a (1,1,1) является

нормальным вектором плоскости. Используя уравнение (4.2):

A(x x0 ) B( y y0 ) C(z z0 ) 0 , получим

1 (x 3) 1 ( y 2) 1 (z 1) 0,

x y z 6 0 - искомое уравнение плоскости.

Ответ: x y z 6 0 .

9.Найти расстояние от точки P( 3,1,1) до точки пересечения плоскости 3x 2y 3z 4 0 с осью Oy .

Решение:

Плоскость пересекается с осью Oy в точке P0 (0, y0 , 0) . Подставим координаты этой точки в уравнение плоскости:

3 0 2 y0 3 0 4 0;2 y0 4 0;

y0 2.

Значит, P0 (0, 2, 0) .

Расстояние d между двумя точками P( 3,1,1) и P0 (0, 2, 0) найдем по формуле (1.1):

d (P, P0 ) (x x0 )2 ( y y0 )2 (z z0 )2 , в нашем случае

d(P, P0 ) ( 3 0)2 (1 ( 2))2 (1 0)2 9 9 1 19 .

Ответ: d (P, P0 ) 19 .
10.Найти угол между прямой	x		y 5	z 3	и плоскостью
10.Найти угол между прямой				1	и плоскостью
	1	2		1

2x y z 4 0 .

Решение:
Угол между прямой и плоскостью находят по формуле		(5.5).
Направляющий	вектор прямой a (1, 2, 1) , нормальный	вектор
плоскости n (2,	1, 1) .

sin		Al Bm Cn			1 2 2 ( 1) 1 1	1
		Al Bm Cn			1 2 2 ( 1) 1 1


	l2 m2 n2		A2 B2 C2	12 22 ( 1)2 22 ( 1)2 12 6

Значит, arcsin 16 .

Ответ: arcsin 16 .

11.Составить уравнения прямой, проходящей через точку P(2,1, 3)

x 2 y z 0;

параллельно прямой

y 4z 2 0.

Решение:

x 2 y z 0;

Прямая задана пересечением двух плоскостей

y 4z 2 0.

Ее направляющий вектор a n1 n2 , где n1 (1, 2,1) и n2 (0,1, 4) - нормальные векторы данных плоскостей. Векторное произведение найдем по формуле (2.8):

	i	j	k
a	1 2		1	8i 0 j 1k 0k 1i ( 4) j 7i 4 j k ,
	0	1 4

a (7, 4,1) .

Искомая прямая параллельна данной, значит, в качестве ее направляющего вектора можно взять найденный направляющий вектор

a (7, 4,1) .

Воспользуемся каноническими уравнениями прямой (5.1):

x x0	y y0	z z0	, подставив координаты точки	P(2,1, 3) , лежащей на
l	m	n

этой прямой, и координаты направляющего вектора прямой a

Получим

x 2

y 1

z 3

- уравнения искомой прямой.

Ответ:

x 2

y 1

z 3

12.Доказать,

что прямые

x 2

z 3

x y 2 0;

2x 2z 0

перпендикулярны.

Решение:

(7, 4,1) .

взаимно

Условие перпендикулярности двух прямых (5.10):

l1l2 m1m2 n1n2 0 ,

где l1, m1, n1 и l2 , m2 , n2 - координаты направляющих векторов прямых.

Направляющий вектор первой прямой a1 (1, 2, 1) , так как прямая задана каноническими уравнениями.

Чтобы найти направляющий вектор второй прямой, заданной пересечением двух плоскостей, нужно найти векторное произведение нормальных векторов этих плоскостей. Нормальные векторы n1 (1, 1, 0) и

n2	(2,		0, 2) .
		i	j k
		i	j k
a2		1	1 0	2i 0 j 0k 2k 0i ( 2) j 2i 2 j 2k ,
		2	0 2

a2	( 2, 2, 2) .

Подставим координаты a1 и a2 в формулу (5.10):

1 ( 2) 2 2 1 ( 2) 2 4 2 0 .

Условие выполнено, значит, прямые перпендикулярны.

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

Соседние файлы в предмете Аналитическая геометрия

#
29.03.2016321.56 Кб62Programma_KR_po_anal_geom_i_lin_algebre.pdf
#
11.02.20151.93 Mб373Методичка по аналитической геометрии.pdf