
Методичка по аналитической геометрии
.pdf
x 1 0 t, y 2 1t или |
x 1, y 2 t |
- |
искомые параметрические |
уравнения. |
|
|
|
Ответ: x 1, y 2 t . |
|
|
|
* Проведем радиус-векторы в точки M 0 |
и |
M1 , принадлежащие прямой L |
|
(рис. 8). Обозначим OM0 r0 , OM1 r. Вектор M0M1 (x1 x0 , y1 y0 ) коллинеарен
направляющему вектору a (l, m) , т.е. вектор M0M1 ta . |
Из треугольника OM0 M1 |
||
получим по правилу сложения векторов OM1 OM0 M0M1 |
или |
||
|
|
|
|
|
r r0 ta |
|
(3.8) |
|
|
|
|
- векторное уравнение прямой, где r0 - радиус-вектор точки M 0 , лежащей на прямой, a – направляющий вектор прямой L.
Подведем итог.
Виды уравнений прямой на плоскости:
1.x a - уравнение прямой, перпендикулярной оси Ox .
2.y b - уравнение прямой, параллельной оси Ox .
3. y kx b - уравнение прямой с заданным угловым коэффициентом, где k - угловой коэффициент прямой.
4. |
|
y y0 |
k(x x0 ) |
- уравнение прямой, проходящей через точку |
|||||||||
|
M0 (x0 , y0 ) с заданным угловым коэффициентом k . |
||||||||||||
5. |
|
x x0 |
|
|
y y0 |
- уравнение прямой, проходящей через 2 заданные |
|||||||
|
x x |
|
y y |
||||||||||
|
|
|
|
|
|
|
|
||||||
|
1 |
0 |
1 |
0 |
|
|
|
||||||
|
точки M0 (x0 , y0 ) и M1 (x1, y1 ) . |
|
|||||||||||
6. |
|
x x0 |
|
|
|
y y0 |
|
- |
каноническое уравнение |
прямой, проходящей |
|||
|
|
l |
|
|
|||||||||
|
|
|
|
|
|
m |
|
|
|
||||
|
через точку M0 (x0 , y0 ) с направляющим вектором a (l, m) . |
||||||||||||
7. |
|
x x0 |
lt, |
y y0 |
mt - параметрические |
уравнения прямой, |
|||||||
проходящей через точку M0 (x0 , y0 ) с направляющим вектором
a (l, m) .
30

8. |
A(x x0 ) B( y y0 ) 0 - уравнение прямой, проходящей через |
|
|
точку M0 (x0 , y0 ) |
с нормальным вектором n ( A, B) . |
9. |
Ax By C 0 |
- общее уравнение прямой, где А и В |
координаты нормального вектора прямой.
10. r r0 ta - векторное уравнение прямой, где r0 - радиус-вектор точки M 0 , лежащей на прямой, a – направляющий вектор прямой L.
Взаимное расположение прямых на плоскости
Вычисление угла между прямыми
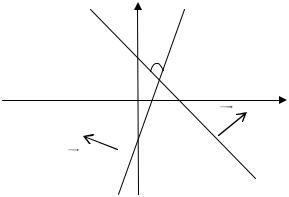
Определение. Углом между прямыми называется наименьший из двух смежных углов, образованных прямыми.
y |
n2 L2 |
L1 |
|
|
|
a1 |
|
n1 |
1 |
2 |
x |
a2
|
|
|
Рис. 14 |
|
|
|
|
На рисунке 14 - угол между прямыми. Пусть прямые L1 и L2 |
|||||||
заданы уравнениями с угловыми коэффициентами: |
|
||||||
L1 : y k1x b1, |
k1 tg 1 |
|
|
|
|
|
|
L2 : y k2 x b2 , |
k2 tg 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg |
|
k2 k1 |
|
|
|
|
|
1 k1k2 |
. |
|
(3.9) |
||
|
|
|
|
||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
31 |
|
|
|
|||
Формула (3.9) определяет угол между прямыми, если известны их угловые коэффициенты.
Если прямые параллельны, то 1 2 , а следовательно,
k1 k2 |
(3.10) |
|
|
- условие параллельности двух прямых, заданных уравнениями с угловыми коэффициентами.
Если прямые перпендикулярны, то тангенс угла между ними не
существует, т.е. знаменатель формулы tg |
k2 k1 |
равен нулю 1 k k |
|
0 , |
|
2 |
|||
1 k1k2 |
1 |
|
||
|
|
|
||
отсюда |
|
|
|
|
k |
|
1 |
|
|
|
|
(3.11) |
||
1 |
|
k2 |
||
|
|
|
||
- условие перпендикулярности двух прямых, заданных уравнениями с угловыми коэффициентами.
Пусть прямые заданы общими уравнениями.
L1 : A1x B1 y C1 0;
L2 : A2 x B2 y C2 0.
В этом случае задача об определении угла между прямыми сводится к определению угла между нормальными векторами.
L2 |
y |
L2 |
x
n2
n1
Рис. 15
32
Из курса векторной алгебры известно, что угол между векторами находят, используя скалярное произведение векторов:
cos |
n1 |
|
n2 |
. |
|
|
|
|
|
|
|
|
|
n1 |
|
n2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
А так как из уравнений прямых n1 A1, B1 |
и n2 |
A2 , B2 , то |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
cos |
|
A1 A2 B1 B2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
(3.12) |
|
|
|
|
|
|
A2 |
B2 |
A2 B2 |
|
|||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
1 |
1 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- формула для вычисления угла между прямыми, заданными общими уравнениями.
Если прямые параллельны, то векторы n1 A1, B1 |
и n2 A2 , B2 |
коллинеарны (рис. 16). Значит, их координаты пропорциональны,
т.е.
|
A1 |
|
B1 |
|
|
|
A2 |
B2 |
(3.13) |
||
|
|
||||
|
|
|
|||
|
|
|
|
|
|
- условие параллельности прямых, заданных общими уравнениями.
y |
L1 L2 |
n1 n2
x
Рис. 16
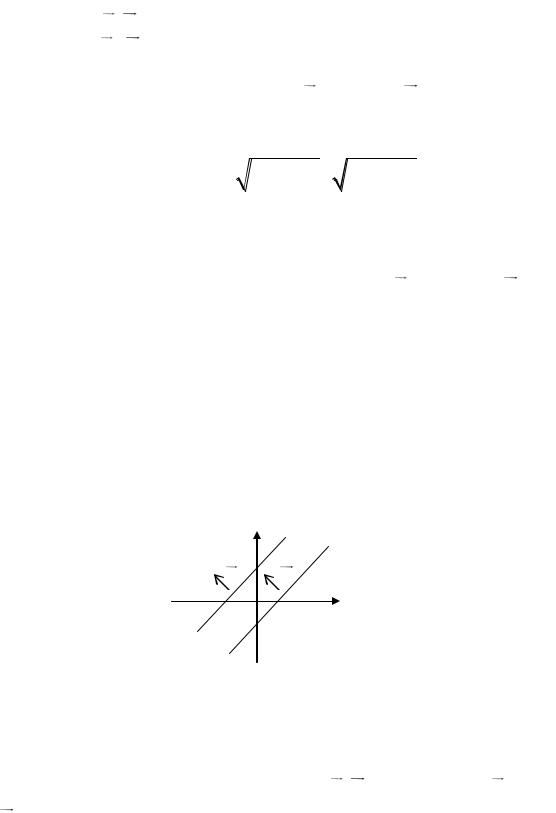
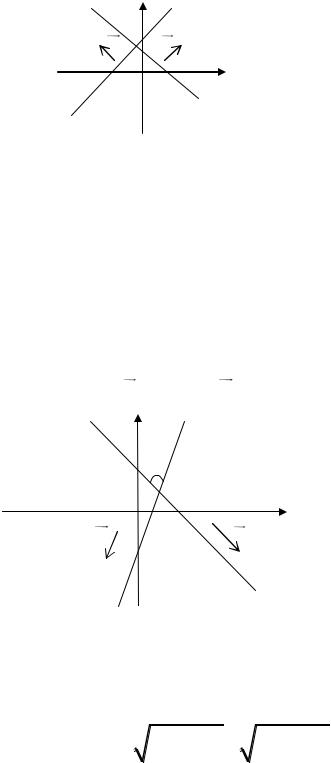
Если прямые перпендикулярны (рис. 17), значит, угол между ними равен 2 . Следовательно, скалярное произведение нормальных
векторов этих прямых равно нулю, т.е. n1 n2 0 . А так как n1 A1, B1 и
n2 A2 , B2 , то
33
|
A1 A2 |
B1 B2 |
0 |
(3.14) |
|
|
|
||
- условие перпендикулярности прямых, заданных общими |
||||
уравнениями. |
|
|
|
|
|
L1 y |
L2 |
|
|
n2 n1
x
Рис. 17
Пусть прямые заданы каноническими уравнениями.
L : |
|
x x1 |
|
|
y y1 |
; |
||
|
|
|
|
|||||
1 |
|
l1 |
|
|
m1 |
|||
|
|
|
|
|||||
L : |
x x2 |
|
y y2 |
. |
||||
|
|
|||||||
2 |
|
l2 |
|
|
m2 |
|||
|
|
|
|
|||||
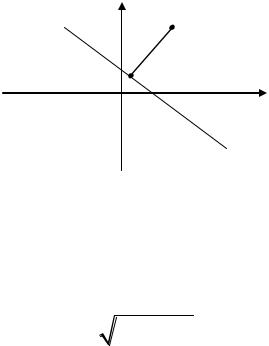
По полной аналогии с предыдущим случаем задача об определении угла между прямыми сводится к определению угла между направляющими векторами a1 l1, m1 и a2 l2 , m2 (рис. 18).
L2 |
y |
L2 |
a2 |
a1 |
Рис. 18
Угол между прямыми находят по формуле
|
|
|
|
|
||||||
cos |
|
l1 l2 m1 m2 |
|
|||||||
|
|
|
|
|
|
|
|
|
||
2 |
2 |
|
2 |
2 . |
(3.15) |
|||||
|
||||||||||
|
l1 |
m1 |
l2 |
m2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
34 |
|
|
|
|
|
|
|
Условие параллельности двух прямых:
|
|
|
l1 |
|
m1 |
|
|
|
|
|
|
|
l |
m . |
|
|
(3.16) |
||
|
|
|
|
|
|
||||
|
|
2 |
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Условие перпендикулярности двух прямых: |
|
||||||||
|
|
|
|
|
|
|
|
||
|
l1 l2 |
m1 m2 |
0 . |
(3.17) |
|||||
|
|
|
|
|
|
|
|
|
|
Расстояние от точки до прямой.
Пусть прямая задана общим уравнением Ax By C 0 . Точка N1 (x1, y1 ) не принадлежит прямой (рис. 19).
L |
y |
N1 |
N2 x
Рис. 19
Расстояние от точки N1 (x1, y1 ) до прямой вычисляется по формуле:
|
d |
|
Ax1 By1 C |
|
|
|
|
(3.18) |
|||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
A2 B2 |
|
||||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
- формула расстояния от точки N1 (x1, y1 ) |
до прямой Ax By C 0 . |
||||||||||
Пример. Найти расстояние от точки |
N1 ( 6, 3) |
до прямой, заданной |
|||||||||
уравнением 3x 4y 15 0 . |
|
|
|
|
|
|
|
|
|
||
Решение: По формуле (3.18) расстояние от точки до прямой:
35
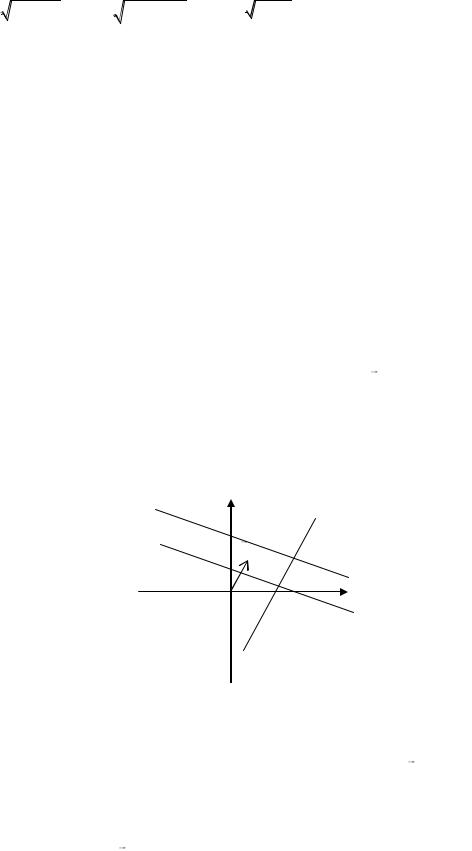
d |
|
Ax1 By1 C |
|
|
|
3 ( 6) 4 3 15 |
|
|
|
18 12 15 |
|
|
|
15 |
|
3 . |
|||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
A2 |
B2 |
|
32 |
( 4)2 |
9 |
16 |
5 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Ответ: d 3.
Решение задач.
1. Дана прямая L : x 3y 4 0 . Составить уравнение прямой, проходящей через точку M0 ( 2, 5) :
а) параллельно данной прямой L ;
б) перпендикулярно данной прямой L .
Решение:
Прямая |
L задана |
общим уравнением x 3y 4 0 . Следовательно, |
можно |
определить |
ее нормальный вектор n (1, 3) (координаты |
нормального вектора – это коэффициенты при x и y в общем уравнении прямой).
А. Пусть L1 - искомая прямая (рис. 20).
L1 |
y |
L2 |
L |
|
n |
|
|
x |
|
|
|
Рис. 20 |
|
|
|
Поскольку прямые L и L1 |
параллельны, то их нормальные векторы |
|||||
коллинеарны (в частности, |
равны). |
Значит, вектор n (1, 3) |
является |
|||
нормальным вектором и прямой L и прямой L1 . Так как известна точка |
||||||
M0 ( 2, 5) , которая принадлежит искомой прямой L1 |
и нормальный вектор |
|||||
этой |
прямой |
n (1, 3) , |
то |
используем |
уравнение |
(3.5): |
|
|
|
36 |
|
|
|

A(x x0 ) B( y y0 ) 0 - уравнение прямой, проходящей через точку M0 (x0 , y0 ) с нормальным вектором n ( A, B) .
Подставив координаты точки и координаты нормального вектора в это уравнение, получим:
1 (x ( 2)) 3 ( y 5) 0;
x2 3y 15 0;
x3y 13 0 - уравнение искомой прямой L1 .
Как видим, уравнения параллельных прямых отличаются только свободными членами.
Б. Пусть прямая L2 |
перпендикулярна данной прямой L (рис. 18). Тогда |
|||||||||||||||||||
нормальный вектор прямой L расположен параллельно прямой L2 , |
||||||||||||||||||||
значит, |
он |
является направляющим |
вектором |
для |
прямой L2 , |
т.е. |
||||||||||||||
a n (1,3) . |
Таким образом, |
для прямой L2 |
известна точка |
M0 ( 2, 5) , |
ей |
|||||||||||||||
принадлежащая, и |
направляющий |
вектор a (1,3) . |
Воспользуемся |
|||||||||||||||||
каноническим уравнением |
прямой (3.6): |
x x0 |
|
|
y y0 |
. |
Подставляя |
|||||||||||||
l |
m |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
координаты точки |
x0 2, y0 5 |
и координаты направляющего вектора |
||||||||||||||||||
l 1, m 3 в это уравнение, получим: |
|
|
|
|
|
|
|
|
||||||||||||
|
x 2 |
|
y 5 |
- уравнение искомой прямой L . |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
|
|
3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ: А. x 3y 13 0 ; Б. |
|
x 2 |
|
y 5 |
. |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
1 |
3 |
|
|
|
|
|
|
|
|
|||
2. Составить уравнение высоты AD и медианы AK треугольника
ABC , если A( 1, 2), B(6, 6), C( 3,9) .
Решение:
Рассмотрим треугольник ABC (рис. 21).
37
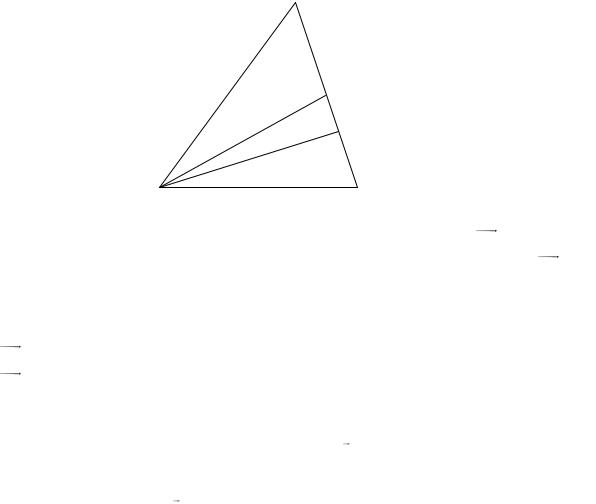
B
K
D
A |
Рис. 21 |
C |
|
|
|
||
AD - высота треугольника ABC , т.е. |
AD BC . Значит, вектор BC является |
||
нормальным вектором для прямой AD . Найдем координаты вектора BC . Чтобы найти координаты вектора, нужно из координат конца этого вектора вычесть координаты начала, т.е.
BC ( 3 6, 9 6);
BC ( 9,3) n.
Так как известна точка A( 1, 2) , которая принадлежит искомой прямой AD , и нормальный вектор этой прямой n ( 9, 3) , то воспользуемся уравнением (3.5) прямой, проходящей через точку M0 (x0 , y0 ) с нормальным вектором n ( A, B) : A(x x0 ) B( y y0 ) 0.
Подставим координаты точки x0 9, y0 3 и координаты нормального вектора A 9, B 3 в уравнение и получим:
9 (x ( 1)) 3 ( y 2) 0; 9x 9 3y 6 0;
9x 3y 15 0 - уравнение высоты AD . |
|
||||||||||||||
AK - медиана треугольника ABC , значит, точка |
K является серединой |
||||||||||||||
отрезка |
BC . |
|
Найдем координаты точки |
K по формулам |
|||||||||||
x |
x1 x2 |
, y |
y1 y2 |
. |
|
|
|
||||||||
|
|
|
|
|
|
||||||||||
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
x |
|
|
xB xC |
|
6 3 |
|
3 |
1,5, |
|
||||||
K |
2 |
|
|
|
2 |
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
y |
|
|
yB yC |
|
6 9 |
|
15 |
7,5. |
|
||||||
K |
2 |
|
2 |
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
38 |
|

K(1,5, 7,5)
Поскольку известны координаты двух точек A и K прямой, то воспользуемся уравнением (3.3) прямой, проходящей через 2 заданные
точки: |
x x0 |
|
y y0 |
, где (x , y ) |
- координаты |
точки А, (x , y ) - |
||||||||||||
|
|
|
||||||||||||||||
|
|
|
|
|
|
x1 x0 |
0 |
0 |
|
|
|
|
1 |
1 |
||||
|
|
|
|
|
|
y1 y0 |
|
|
|
|
|
|
|
|||||
координаты точки В. |
|
|
|
|
|
|
|
|||||||||||
Подставим координаты точек A(1, 2) |
и K(1,5, 7,5) |
в это уравнение: |
|
|||||||||||||||
|
x (1) |
|
|
|
y 2 |
; |
|
|
|
|
|
|
|
|
||||
1,5 (1) |
7,5 2 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x 1 |
|
y 2 |
; умножая обе части этого уравнения на |
1 |
, получим: |
|
|||||||||||
|
|
|
|
|
2 |
|
||||||||||||
2,5 |
|
5,5 |
|
|
|
|
|
|
|
|
|
|
||||||
|
x 1 |
|
y 2 |
- уравнение медианы AK . |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
5 |
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ: 9x 3y 15 0 - уравнение высоты |
AD ; |
|
|
|
|
|||||||||||||
|
x 1 |
|
y 2 |
- уравнение медианы AK . |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
5 |
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
3. |
Найти точку пересечения с осью Ox |
прямой, проходящей через |
||||||||||||||||
|
|
|
точку M (5, 1) , перпендикулярно прямой x 1 4t, y 2t . |
|
||||||||||||||
Решение:
Данная прямая задается параметрическими уравнениями. Направляющий вектор этой прямой a (4, 2) (коэффициенты перед параметром t в уравнениях). Так как по условию прямые перпендикулярны, то данный
вектор |
a (4, 2) |
будет |
являться |
нормальным вектором |
для искомой |
||
прямой, |
значит, |
n (4, 2) . |
Используем |
уравнение |
(3.5): |
||
A(x x0 ) B( y y0 ) 0 |
- уравнение прямой, |
проходящей |
через |
точку |
|||
M (x0 , y0 ) с нормальным вектором n ( A, B) , подставив в него координаты данной точки M (5, 1) и координаты нормального вектора n (4, 2) .
Для нашей прямой:
4 (x ( 5)) 2 ( y ( 1)) 0 ;
4 (x 5) 2 ( y 1) 0 ;
39
