Методичка по аналитической геометрии
.pdfТ. В. Бубнова, Ю. А. Виноградова
Аналитическая геометрия
Избранные главы
Москва
2012
0
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
Московский государственный технологический университет
«СТАНКИН»
Т. В. Бубнова, Ю. А. Виноградова
Аналитическая геометрия
Избранные главы
Допущено Учебно-методическим объединением по образованию в области автоматизированного машиностроения (УМО АМ) в качестве учебного пособия для студентов высших учебных заведений,
обучающихся по направлению подготовки: бакалавров и магистров
«Техносферная безопасность», «Защита окружающей среды», «Технология, оборудование и автоматизация машиностроительных производств» и дипломированных специалистов «Конструкторско-
технологическое обеспечение машиностроительных производств», «Проектирование технологических машин и комплексов».
Москва
2012
1
УДК 513
ББК 22.151 С23
Рецензенты: д-р ф.-м. н., проф. Л. Ю. Васильева (кафедра общей физики МФТИ); доц. Смирнова М. А. (кафедра информатики и прикладной математики
Тверского государственного технического университета)
Бубнова Т. В., Виноградова Ю. А.
С23 Аналитическая геометрия. Избранные главы: учеб. пособие / Т. В. Бубнова, Ю. А. Виноградова. – М.: ФГБОУ ВПО МГТУ
«СТАНКИН», 2012. – 87 с.: ил.
Содержит теоретический минимум для решения задач по аналитической геометрии, а также примеры решения всех типов задач, встречающихся в контрольной работе, приводятся задачи для самостоятельного решения.
Для использования на практических занятиях и самостоятельной работы студентов.
УДК 513
ББК 22.151
©Бубнова Т. В., Виноградова Ю. А., 2012
©ФГБОУ ВПО МГТУ «СТАНКИН», 2012
2
|
Содержание |
|
1. |
Простейшие задачи аналитической геометрии |
.............................................4 |
2. |
Векторы ............................................................................................................. |
9 |
3. |
Прямая на плоскости...................................................................................... |
23 |
4. |
Плоскость в пространстве. ............................................................................ |
44 |
5. |
Прямая в пространстве................................................................................... |
53 |
6. |
Полярные координаты ................................................................................... |
75 |
7. |
Параметрические уравнения линии.............................................................. |
83 |
Библиографический список............................................................................... |
87 |
|
3
1. Простейшие задачи аналитической геометрии
Расстояние между двумя точками
Если в пространстве Oxyz задана декартова система координат и точки M1 (x1, y1, z1 ) и M2 (x2 , y2 , z2 ) (рис.1),
z
M 2
M1
y
x
Рис. 1
то расстояние между ними вычисляется по формуле
|
|
|
|
|
|
|
|
|
|
|
d(M |
, M |
2 |
) (x x )2 |
( y y )2 |
(z |
2 |
z )2 |
(1.1) |
||
1 |
|
2 1 |
2 1 |
|
1 . |
|||||
|
|
|
|
|
|
|
|
|
|
|
Расстояние между двумя точками в плоскости Oxy :
|
|
|
|
|
|
|
|
d(M |
, M |
2 |
) (x x )2 |
( y y )2 |
(1.1’) |
||
1 |
|
2 1 |
2 1 . |
||||
|
|
|
|
|
|
|
|
Деление отрезка в данном отношении
Рассмотрим отрезок M1M2 , лежащий на некоторой прямой. Пусть M - любая, отличная от M 2 , точка прямой.
M1 |
M M2 |
Рис.2
4
Точка M делит отрезок |
M1M2 |
в отношении , если |
M1M |
. |
||
MM |
2 |
|||||
|
|
|
|
|||
Координаты этой точки вычисляют по формулам:
|
x x |
|
y y |
z z |
2 |
|
|
||
x |
1 2 |
, |
y |
1 2 |
, z |
1 |
. |
(1.2) |
|
1 |
1 |
1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
Формулы (1.2) называются формулами деления отрезка в данном отношении.
Если точки расположены в плоскости Oxy , то формулы (1.2) принимают вид:
x |
x x |
y |
y y |
|
||
1 2 |
, |
1 2 |
. |
(1.2’) |
||
1 |
1 |
|||||
|
|
|
|
|
|
|
При 1 точка M делит отрезок пополам. Тогда координаты середины отрезка определяют следующим образом:
x |
x1 x2 |
, y |
y1 y2 |
, z |
z1 z2 |
|
|
|
|
|
|
||||
2 |
2 |
2 . |
(1.3) |
||||
Формулы (1.3) называются формулами деления отрезка пополам. В случае плоскости Oxy формулы (1.3) принимают вид:
x |
x1 x2 |
, y |
y1 y2 |
|
|
|
|
|
|||
2 |
2 . |
(1.3’) |
|||
5
Решение задач.
1.Найти длину медианы АD треугольника АВС с вершинами А(2, 1,
0), В(-1, -1, 2) и С(3, -5, 4).
Решение:
В
D
По условию AD – медиана Следовательно, точка D делит отрезок ВС пополам. По формуле (1.3’) найдем координаты точки D:
A |
|
|
|
|
|
|
C |
|
|
|
|
|
|
||
|
|
|
|
Рис.3 |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
xB xC |
|
1 3 |
1, y |
|
|
yB yC |
|
1 5 |
3, |
|||
D |
2 |
|
2 |
|
D |
2 |
2 |
||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
z |
|
|
|
zB zC |
|
2 4 |
3. |
|
|
|
|
|
|
||
D |
|
2 |
|
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
D(1, 3,3) . Нахождение длины медианы сводится к нахождению расстояния между точками А и D. Воспользуемся формулой (1.1).
AD 
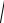(xD xA )2 ( yD yA )2 (zD zA )2 
(1 2)2 ( 3 1) 2 (3 0)2
1 16 9 
26.
Ответ: AD 
26 .
2. Найти координаты точки пересечения медиан треугольника с вершинами А(3, -4), В(11, 2) и С(1, 8).
Решение:
Пусть BM и AL - медианы треугольника АВС (рис. 4).
6
В
ОL
|
|
|
|
|
|
|
|
|
|
A |
|
M |
C |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4 |
|
|
Точка О пересечения медиан треугольника делит медиану BM в |
|||||||||||||||
отношении 2:1, т.е. |
BO |
|
|
2 |
. |
|
|
||||||||
OM |
1 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
Точка М делит сторону AC пополам. Пользуясь формулами (1.3’), |
|||||||||||||||
находим координаты точки М. |
|
|
|
||||||||||||
x |
xA xC |
|
3 1 |
2, |
y |
|
|
yA yC |
|
4 8 |
2. |
||||
|
|
M |
|
|
|
|
|
||||||||
M |
2 |
|
2 |
|
|
|
|
|
2 |
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
Теперь применим формулы (1.2’) для нахождения координат точки О.
x |
xB xM |
|
11 4 |
5, |
y |
yB yM |
|
2 4 |
2. |
|
1 |
1 2 |
1 |
1 2 |
|||||||
O |
|
|
O |
|
|
|||||
|
|
|
|
|
|
|
|
Ответ: O(5, 2) .
3.Даны точки А(-6, 1, -4) и С(2, 1, -2). Точка С делит отрезок АВ в отношении 3. Найти координаты точки В.
Решение:
Точка С делит отрезок АВ в отношении 3, т.е. CBAC 3 .
Воспользуемся формулами (1.2):
x |
xA xB , y |
yA yB , z |
zA zB . |
|||||
C |
|
1 |
C |
|
1 |
C |
|
1 |
|
|
|
|
|
|
|||
Подставим координаты точек А, С и 3 в эти формулы. Получим уравнения для определения координат точки В:
2 6 3 xB ; 1 |
1 3 yB |
; 2 |
4 3 zB |
x |
14 |
; y |
|
1; z |
|
4. |
||
|
|
|
B |
B |
||||||||
4 |
|
4 |
|
4 |
B |
3 |
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
Ответ: B( |
14 |
, 1, 4) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
4.Найти точку М, симметричную точке N(-2, 1) относительно точки K(-5, 3).
Решение: Точка М симметрична точке N относительно точки К, если точки M, N, K лежат на одной прямой и точка К делит отрезок MN пополам. Используем формулы (1.3’) для определения координат середины отрезка:
x |
|
xN xM |
; y |
|
|
yN yM |
. Подставляя в эти соотношения координаты |
|||
|
|
K |
|
|
||||||
K |
|
|
2 |
|
|
2 |
|
|||
|
|
|
|
|
|
|
||||
точек N и K, получим уравнения: |
||||||||||
5 |
|
2 xM |
; 3 |
1 yM |
, из которых найдем координаты точки М: |
|||||
|
2 |
2 |
||||||||
|
|
|
|
|
|
|
|
|||
xM 8, yM 5.
Ответ: M ( 8,5) .
Задачи для самостоятельного решения
1. A 2;1 , B 6; 3 . Точка С делит отрезок АВ в отношении 3. Найти координаты точки С.
|
|
Ответ: C(4, 2) . |
|||||
2. |
Даны точки |
A ( 6; 2; 4) и B (1; 2; 2) .Найти координаты точки С, |
|||||
|
делящей отрезок АВ в отношении 5. |
|
|
|
|
|
|
|
|
Ответ: C( |
1 |
, 2, 1) . |
|||
|
|
|
|||||
|
|
|
6 |
|
|||
3. |
Найти точку |
A1 , симметричную точке A ( 2;1) относительно точки |
|||||
|
B (3; 3) . |
|
|
|
|
|
|
|
|
Ответ: |
A1(8, 5) . |
||||
4. |
A 1;1; 2 , B (2;1; 1) , C ( 3;1; 0) . Найти длину медианы треугольника |
||||||
|
АВС, проведенной из вершины В. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
13 . |
|
|||
5.Точка B симметрична точке A ( 4; 1; 3) относительно оси Ox . Найти координаты точки B .
Ответ: B( 4, 1, 3)
8
2. Векторы
Определение. Геометрическим вектором (или просто вектором)
называется направленный отрезок. Вектор, начало которого в точке А, а конец – в точке В, обозначается AB . Также векторы обозначаются строчными буквами, например, a . Начало вектора называется точкой его приложения. Длина отрезка АВ называется длиной или модулем вектора AB и обозначается через | AB | . Длина вектора a обозначается через | a | .
Всякий геометрический вектор определяется точкой приложения, длиной и направлением.
Вектор, длина которого равна единице, называется единичным вектором.
Определение. Два вектора называются равными, если они имеют одинаковые длины и одинаковые направления.
Определение. Векторы, противоположно направленные и имеющие равные длины, называются противоположными. Вектор, противоположный вектору a , обозначается a .
Линейные операции над векторами
Определение. Суммой двух векторов a и b называется вектор a b , который определяется по “правилу треугольника” (рис. 5):
OA AB OB
(если a OA, b AB , то a b OB ).
b В
А
a |
a b |
|
О
Рис. 5
9