Методичка по аналитической геометрии

A(x x0 ) B( y y0 ) C(z z0 ) 0 , подставив в него координаты точки M (1, 2,3) , принадлежащей искомой плоскости, и координаты нормального вектора n KN 2, 2, 0 :

2 (x 1) 2 ( y 2) 0 (z 3) 0,

2x 2y 2z 6 0 - искомое уравнение плоскости.

Ответ: 2x 2y 2z 6 0 .

4.Составить уравнение плоскости, проходящей через точку P(1, 2, 3) параллельно плоскости 4x 5z 7 0 .

Решение:

Плоскость задана общим уравнением 4x 5z 7 0 .

Коэффициенты при x, y, z в этом уравнении есть координаты нормального вектора этой плоскости, т.е. n1 (4, 0, 5) .

Поскольку плоскости параллельны, то в качестве нормального вектора для искомой плоскости n2 мы можем использовать вектор n1 - нормальный вектор заданной плоскости, т.е. n2 (4, 0, 5) .

Применяя уравнение (4.2): A(x x0 ) B( y y0 ) C(z z0 ) 0 , получим:

4 (x 1) 0 ( y 2) ( 5) (z ( 3)) 0,

4x 5z 11 0 - искомое уравнение плоскости.

Ответ: 4x 5z 11 0 .

5.Точка М симметрична точке N(1, 2, 4) относительно оси Ox . Составить уравнение плоскости, проходящей через точку М перпендикулярно оси Oy .

Решение:

Так как точка М симметрична точке N относительно оси Ox , то точка М имеет координаты M (1, 2, 4) (рис. 24).

50

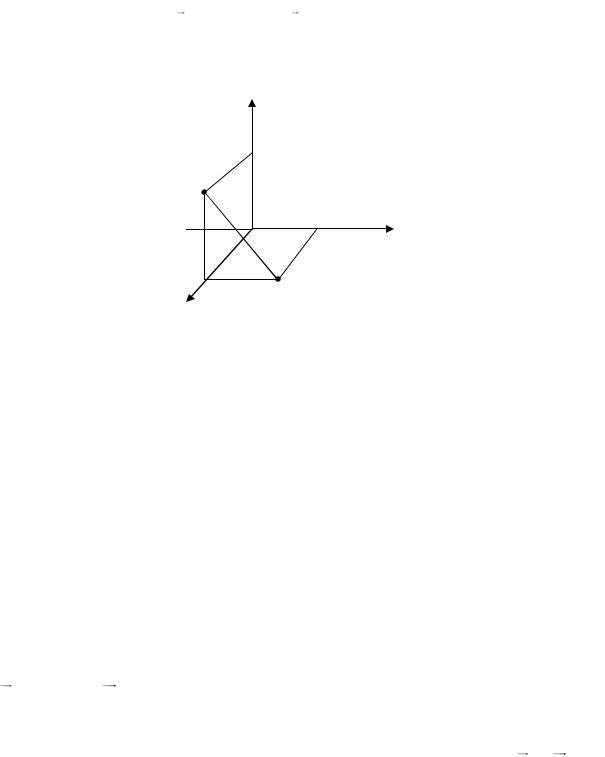
Плоскость перпендикулярна оси Oy , следовательно, в качестве нормального вектора можем взять любой из векторов, лежащих на оси Oy , например, вектор j (0, 1, 0) , т.е. n (0, 1, 0) .

z

N

Рис. 24

Пользуясь уравнением (4.2): A(x x0 ) B( y y0 ) C(z z0 ) 0 , получим:

0 (x 1) 1 ( y 2) 0 (z 4) 0,

y 2 0 - искомое уравнение плоскости.

Ответ: y 2 0 .

6.При каком значении плоскости 3x y 6z 2 0 и x 4y 2z 1 0 параллельны?

Решение:

Условием параллельности двух плоскостей является коллинеарность их нормальных векторов. Нормальные векторы данных плоскостей:

n1 (3, , 6) и n2 (1, 4, 2) .

Два вектора коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны. Для векторов n1 и n2

Ответ: 12.

51

через середину отрезка АВ перпендикулярно оси Oy . Ответ: y 3 0 .

3.Составить уравнение плоскости, проходящей через точку M ( 2; 2; 3) параллельно плоскости 3x y 4z 3 0 .

Ответ: 3x y 4z 8 0 .

4.Составить уравнение плоскости, проходящей через точку M ( 1; 2; 3) перпендикулярно радиус-вектору этой точки.

параллельны?

Ответ: 12 .

52

5.Прямая в пространстве

Уравнения прямой в пространстве.

Положение прямой линии в пространстве будет определено, если задана точка M 0 на прямой и ненулевой вектор a , которому прямая

параллельна.

z

M 0 M

x

Рис. 25

Определение. Любой ненулевой вектор, лежащий на данной прямой или параллельный ей, называется направляющим вектором этой прямой.

Обозначается a (l, m, n) .

Пусть точка M0 (x0 , y0 , z0 ) принадлежит прямой L (рис. 25).

Точка M (x, y, z) лежит на указанной прямой тогда и только тогда,

когда векторы M0M (x x0 , y y0 , z z0 ) и a (l, m, n) коллинеарны, т.е., их координаты пропорциональны, а именно

53

направляющего вектора. Подставив координаты вектора M0 M1 в уравнение (5.1), получим:

- уравнения прямой, проходящей через две заданные точки

M0 (x0 , y0 , z0 ) и M1 (x1, y1, z1 ) .

Пример.

Составить уравнения прямой, проходящей через точку M0 (1, 0, 1) и

M1 (3, 1, 2) .

Решение:

Воспользуемся уравнением (5.2), где

x0 1, y0 0, z0 1, x1 3, y1 1, z1 2 :

54

Пример.

Составить параметрические уравнения прямой, проходящей через точку

Любые две непараллельные и несовпадающие плоскости определяют прямую как линию их пересечения (рис. 26):

- общие уравнения прямой.

Рис. 26

От общих уравнений прямой можно перейти к каноническим уравнениям прямой. Пусть n1 (A1, B1,C1 ) и n2 ( A2 , B2 ,C2 ) - нормальные векторы плоскостей 1 и 2 .

Для составления канонических уравнений этой прямой нужно:

1.Найти какую-нибудь точку M0 (x0 , y0 , z0 ) , принадлежащую данной прямой. Для этого задаем численное значение одной из

неизвестных x, y, z , две другие находим, решая систему (5.4).

55

2.Найти направляющий вектор a . Прямая L – линия пересечения плоскостей, следовательно, она перпендикулярна каждому из нормальных векторов n1 и n2 . Значит, в качестве направляющего вектора можно взять любой вектор, перпендикулярный векторам n1 и n2 , например, их векторное произведение.

Пример.

Привести к каноническому виду общие уравнения прямой

3x 2 y 4z 5 0,

2x y z 1 0.

Решение:

Найдем координаты точки M 0 , принадлежащей прямой. Пусть z0 0 , тогда

Итак, прямая проходит через точку M0 ( 3, 7, 0) .

Найдем направляющий вектор a .

a ( 6, 11, 1) .

Канонические уравнения прямой, проходящей через точку M0 ( 3, 7, 0) с направляющим вектором a ( 6, 11, 1) :

56

Ax By Cz D 0 (рис. 27).

L

a

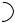
n

Рис. 27

Определение. Углом между прямой и плоскостью называется наименьший из углов, образованных прямой с ее проекцией на эту плоскость.

Обозначим - угол между прямой и перпендикуляром к плоскости.

a (l, m, n) - направляющий вектор прямой L.

n ( A, B,C) - нормальный вектор плоскости .

Угол между векторами a и n находят по формуле

57

- формула для определения угла между прямой и плоскостью.

Если прямая L перпендикулярна плоскости , то векторы a и n коллинеарны, значит, их координаты пропорциональны, т.е.

- условие перпендикулярности прямой и плоскости.

Если прямая параллельна плоскости, то направляющий вектор a прямой перпендикулярен нормальному вектору n плоскости, тогда их скалярное произведение равно нулю, т.е. a n 0 или

- условие параллельности прямой и плоскости.

Если прямая параллельна плоскости и точка M1 (x1, y1, z1 ) , лежащая на прямой, удовлетворяет своими координатами уравнению плоскости, то прямая целиком лежит в этой плоскости.

- условия принадлежности прямой линии плоскости.

Решение:

Направляющий вектор данной прямой a (2, 4, 4) , нормальный вектор плоскости n (4, 3, 6) .

Условие (5.7) не выполняется:

2 4 4 ( 3) 4 ( 6) 28 0 , значит, прямая не параллельна плоскости. Следовательно, прямая пересекает плоскость. Найдем координаты точки пересечения прямой и плоскости. Для этого перейдем от канонических уравнений прямой к параметрическим:

Значит, прямая пересекает плоскость в точке (10, 25, 19) .

Ответ: прямая пересекает плоскость в точке (10, 25, 19) .

Взаимное расположение прямых в пространстве

Рассмотрим две прямые в пространстве, заданные своими каноническими уравнениями:

Прямая L1 проходит через точку M1 (x1, y1, z1 ) , ее направляющий вектор a1 (l1, m1, n1 ) . Прямая L2 проходит через точку M2 (x2 , y2 , z2 ) , ее направляющий вектор a2 (l2 , m2 , n2 ) .

59