Лекция по теории систем 7
.docЛекция №7. Линейные непрерывные стационарные системы в пространстве состояний (микроподход)
Мы рассмотрим
возможность представления системы,
заданной дифференциальным уравнением:
,
с начальными условиями
методом пространства.
Рассмотрим простейший пример колебательной системы:
Введем переменные
состояния:
,тогда
имеем систему уравнений:
В матричном виде:
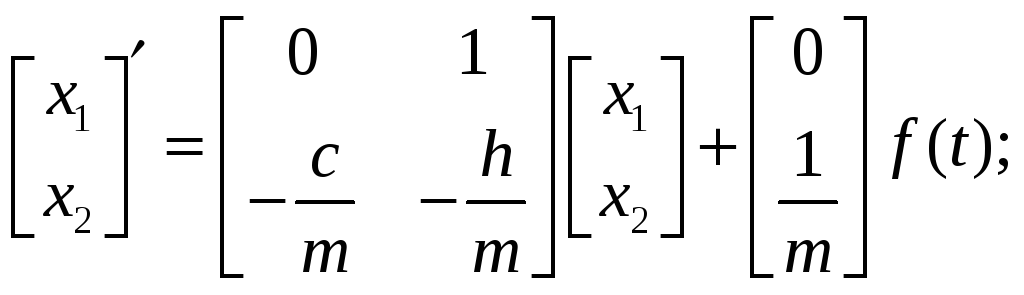(1)
(2)
Уравнение (1) называют уравнением динамики, а уравнение (2) – уравнением выхода.
В общем случае
рассмотрим первоначально уравнение:
, (3)
где
.
Введем переменные состояния следующим
образом:
,
и получим следующую систему дифференциальных уравнений:
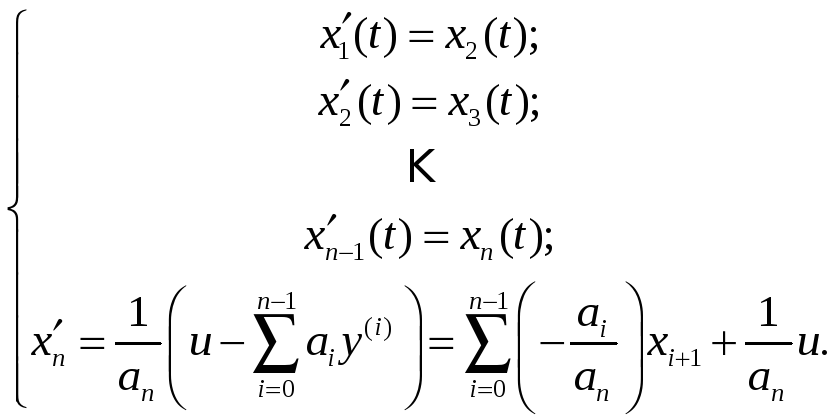
В матричном виде получим:
где
- матрица динамики;
- матрица входа;
- матрица выхода;
- коэффициент усиления по входу.
Приведенная система уравнений задает
представление исходной системы методом
пространства состояний.
При рассмотрении
системы с дополнитель-ным преобразованием
правой части:
,
где
воспользуемся тем, что достаточно
применить преобразование правой части
к переменным состояния (см. предыдущую
лекцию):
Тогда первое уравнение системы
преобразуется к уравнению динамики, а
уравнение выхода приобретает вид:
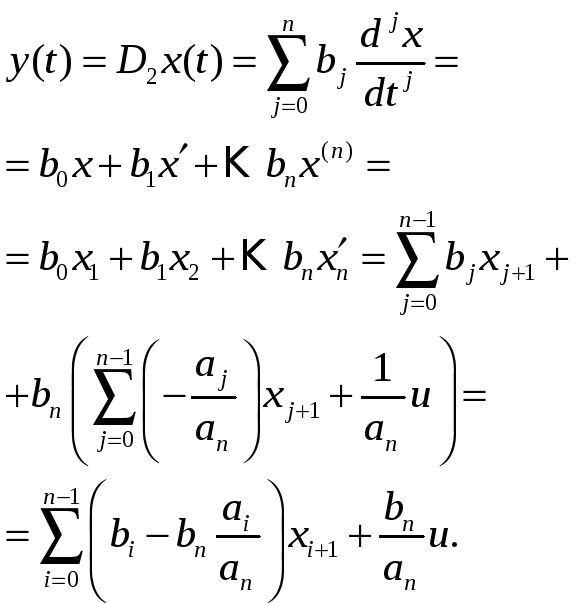
Теперь матрица
выхода
и коэффициент усиления по входу
и снова получаем представление системы
методом пространства состояний:
,
но, естественно, с другими матрицами в
уравнении выхода.
Структурная схема системы, реализующей уравнения динамики и выхода, приведена на рисунке.
Задание 1: Как
изменится уравнение выхода для случая
?
Задание 2:
преобразовать структурную схему для
случая
.
Структурная схема системы, реализующей уравнения динамики и выхода
