1. Теорема о циркуляции в вектора напряжённости электростатического поля

Существуют два равнозначных определения консервативной силы. Оба они подробно обсуждались в механике.

1. Консервативной называется сила, работа которой не зависит от формы траектории.

2. Консервативной называется сила, работа которой на замкнутой траектории равна нулю.

Рассмотрим перемещение заряда qв электростатическом полепо замкнутой траектории (рис. 3.5.). Заряд из точки 1 перемещается по путиL₁в точку 2, а затем возвращается в исходное положение по другому путиL₂. В процессе этого движения на заряд со стороны поля действует консервативная электрическая сила:

.

Работа этой силы на замкнутой траектории L=L₁+L₂равна нулю:

.

Это уравнение, упростив, запишем так:

. (3.18)

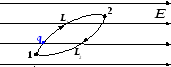
Рис. 3.5.

Разберём подробно последнее уравнение. Подынтегральное выражение — элементарная работа электрической силы, действующей на единичный положительный заряд, на перемещении (рис. 3.6.):

, (3.19)

здесь q= 1 — единичный заряд.

Рис. 3.6.

При подсчёте работы на замкнутой траектории необходимо сложить элементарные работы электрической силы на всех участках траектории. Иными словами, проинтегрировать (3.19) по замкнутому контуру L:

. (3.20)

Интеграл по замкнутому контуру =называется циркуляцией вектора напряжённости электростатического поля по контуруL.По своей сути циркуляция вектора напряжённости — это работа электростатического поля, совершаемая при перемещении по замкнутому контуру единичного положительного заряда.

Так как речь идёт о работе консервативной силы, то на замкнутой траектории она равна нулю:

.

Теорема о циркуляции в электростатике: циркуляция вектора напряжённости электростатического поля по любому замкнутому контуру равна нулю.

2. Связь напряжённости и потенциала электростатического поля

Потенциал и напряжённость — две локальные характеристики электростатического поля. То есть, это две характеристики — энергетическая и силовая — одной и той же точки поля.

Разумно предположить, что между ними должна существовать однозначная связь.

Для отыскания этой связи, вычислим работу электрической силы на элементарном перемещении dlзарядаqв электростатическом поле(рис. 3.7.).

Рис. 3.7.

С одной стороны:

. (3.21)

Но с другой стороны, эту же работу можно связать с разностью потенциалов (₁ – ₂) = –(₂ – ₁) = –d:

. (3.22)

Объединив (3.21) и (3.22), получим:

E_ldl= –d.

Или:

. (3.23)

Важно отметить, что здесь E_l— проекция вектора напряжённости поляна направление перемещения, а— изменение потенциала при переходе в поле из точки 1 в точку 2.

Записав (3.23) для направлений x,yиz, получим соответствующие составляющие (проекции) вектора напряжённости:

(3.24)

Первое уравнение этой системы означает, что проекция вектора напряжённости на ось xравна частной производной потенциала поx, взятой с противоположным знаком.

Полный вектор напряжённости можно, как обычно, представить в виде векторной суммы:

.

Последнее уравнение принято записывать так:

. (3.25)

Здесь векторный оператор «градиент»grad=.

Уравнение (3.25) устанавливает искомую связь двух характеристик электростатического поля — напряжённости и потенциала: напряжённость электростатического поля равна градиенту потенциала с обратным знаком.

До последнего времени мы измеряли напряжённость поля в :

.

Теперь, руководствуясь соотношением (3.23) можно получить ещё одну единицу измерения напряжённости:

.

Несложно показать, что эти две единицы измерения легко превращаются одна в другую:

.