1. Сила Лоренца

Известно, что на каждый элемент тока в магнитном поле действует сила Ампера:

. (9.9)

Если поместить в магнитное поле проводник без тока, то никакой силы мы не обнаружим. Это означает, что магнитное поле «не чувствует» неподвижные заряды. Но стоит им придти в направленное движение, в проводнике появляется ток и на проводник начинает действовать сила (9.9). Можно предположить, что магнитное поле действует на каждый отдельный носитель заряда, направленно движущийся в проводнике, а сила Ампера — интегральный результат сложения всех этих сил. Тогда силу, действующую в магнитном поле на движущийся заряд, можно вычислить, разделив силу Ампера на число носителей заряда dN, движущихся со скоростьюна элементе проводникаdl:

.

Здесь dN=nSdl— число носителей заряда. Вспомнив, чтоI=iS, а плотность токаi=nqV_н, представим (9.8) в таком виде:

. (9.10)

По определению, вектор совпадает по направлению с векторами плотности токаи скорости направленного движения. Поэтому (9.10) можно переписать ещё и так:

.

Теперь, разделив эту силу на число носителей заряда dN, получим силу Лоренца — силу, действующую на зарядq, движущийся со скоростьюв магнитном поле:

. (9.11)

Сила Лоренца пропорциональна заряду движущейся частицы q, её скоростиV_ни величине индукции магнитного поляB. Кроме того, эта сила зависит от угламежду векторамии(рис. 9.2.):

F_Л=qV_нBsin.

Рис. 9.2.

В любом случае сила Лоренца перпендикулярна и вектору и скорости движения частицы. Последний результат представляет особый интерес. Если, то работа такой силы всегда равна нулю:

=0.

Здесь =— угол между векторамии; следовательно,cos= 0 и работа= 0. Это тот случай, когда есть сила, есть перемещение точки её приложения, но работа отсутствует, благодаря особой взаимной ориентации этих двух векторов. Действие такой силы не может привести к изменению величины скорости частицы и её кинетической энергии. Действительно, согласно теореме о кинетической энергии, её изменение равно работе силы:

d_кин=dA.

Но если работа не производится, то и кинетическая энергия не меняется. Неизменность кинетической энергии означает постоянство скорости частицы.

Если заряженная частица движется со скоростью одновременно в двух полях: и в магнитном и в электростатическом, то сила, действующая на неё — сила Лоренца — будет в этом случае складываться из двух сил (опять принцип суперпозиции — теперь сил!):

. (9.12)

2. Теорема Гаусса и теорема о циркуляции магнитного поля. Система уравнений Максвелла электро- и магнитостатики.

Вычислив магнитное поле прямолинейного тока (8.7), мы обнаружили, что силовые линии этого поля — замкнутые окружности, охватывающие проводник с током (рис. 9.3.). Это поле можно «увидеть», разместив вокруг проводника небольшие магнитные стрелки (рис. 9.4.). Они укажут направление магнитных силовых линий в различных точках пространства.

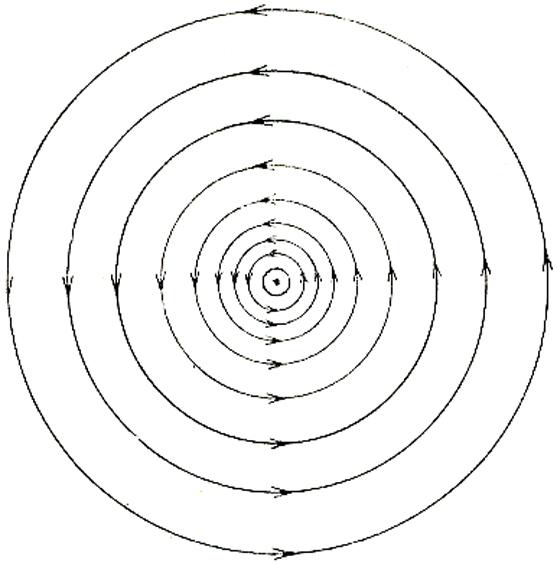
Рис. 9.3.

Рис. 9.4.

Ограниченное число магнитных стрелок можно заменить железными опилками. Каждый такой кусочек металла будет представлять собой магнитную микрострелку, которая будет ориентироваться вдоль магнитных силовых линий поля. На рис. 9.5. представлены магнитные поля кругового тока и катушки с током (соленоида), полученные с помощью таких опилок. Опилки насыпают на лист картона, пронизанный проводником с током. При постукивании по картону опилки распределяются вдоль магнитных силовых линий.

Рис. 9.5.

Присмотревшись к рисункам 9.4. и 9.5., легко обнаружить, что замкнуты не только силовые линии магнитного поля прямолинейного тока, но и силовые линии магнитных полей кругового тока и соленоида.

Можно показать, что замкнутость силовых линий магнитного поля — особенность любых магнитных полей. Здесь уместно напомнить, что силовые линии электростатического поля разомкнуты: они начинаются на положительных зарядах и заканчиваются на отрицательных. Замкнутость магнитных силовых линий приобретает принципиальное значение: из этого свойства следует вывод, что в природе нет магнитных зарядов. Электрические заряды существуют в природе. Они и являются источниками потенциальных электростатических полей. Магнитных зарядов в природе нет. Как же создаются тогда магнитные поля? Их источниками являются электрические токи. В отличие от электростатических полей, магнитные поля не потенциальные.Они называются вихревыми или соленоидальными.

Теперь обратимся к теореме Гаусса для магнитного поля. В этой теореме рассматривается поток вектора магнитной индукции через произвольную замкнутую поверхность:

. (9.13)

На рис. 9.6. замкнутая гауссова поверхность выбрана в магнитном поле прямолинейного тока.

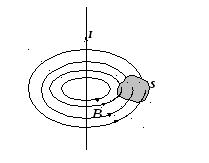
Рис. 9.6.

Если густота магнитных силовых линий соответствует величине вектора магнитной индукции в выбранной точке пространства, то интеграл (9.12) — есть алгебраическая сумма числа силовых линий входящих (–) и покидающих (+) замкнутую поверхность. Учитывая соленоидальность магнитного поля, то есть замкнутость его силовых линий, придём к выводу: число входящих и выходящих силовых линий одинаково и их сумма всегда равна нулю:

. (9.14)

Полученное выражение (9.13) — математическая запись теоремы Гаусса для магнитного поля: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.

Иными словами, эта теорема утверждает: в природе нет магнитных зарядов.

Напомним, что совсем по-другому заканчивается теорема Гаусса для электростатического поля:

.

Поток вектора напряжённости электростатического поля через любую замкнутую поверхность пропорционален величине заряда,заключённого внутри этой поверхности.

Это означает, что электрические заряды — реальность природы, а вот магнитных зарядов в природе нет.

Теорема о циркуляции магнитного поля

Теперь займёмся вычислением циркуляции вектора магнитной индукции по замкнутому контуру. Начнём с простого контура. Пусть для начала контур совпадает с силовой линией магнитного поля прямолинейного тока (рис. 9.7.). По определению, циркуляция вектора по замкнутому контуру равна следующему интегралу:

.

Рис. 9.7.

Обратим внимание на то, что модуль вектора магнитной индукции в нашем случае одинаков во всех точках силовой линии и, следовательно, контура L:

. (9.15)

Согласно (9.8), . Поэтому циркуляцию вектора(9.15) можно записать так:

.

Вывод. В рассмотренном частном случае циркуляция вектора магнитной индукции по замкнутому контуру пропорциональна току, охватываемому этим контуром.

Усложним задачу. Выберем теперь почти произвольный контур L в магнитном поле прямолинейного тока I. Контур по-прежнему охватывает ток и лежит в плоскости, перпендикулярной проводнику с током (рис. 9.8.). Циркуляция на участке контураравна:

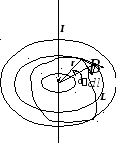
Рис. 9.8.

Здесь =d, поэтому циркуляцию по всему замкнутому контуруLможно записать так:

.

Мы вновь пришли к прежнему результату: циркуляция магнитного поляпо замкнутому контуру пропорциональна току, охватываемому этим контуром.

Что произойдёт, если контур не охватывает ток (рис. 9.9.)?

Рис. 9.9.

Циркуляция на участке по-прежнему будет равна:

.

При обходе такого контура на участке 1-а-2 угол  будет расти от нуля, а на участке 2-b-1 — уменьшаться до нуля. Поэтому циркуляция в этом случае окажется равно нулю:

.

Сделаем ещё одно важное замечание. Циркуляция вектора — скалярная величина. Она может быть положительной и отрицательной.

Циркуляция положительна, когда направление обхода контура связано с направлением тока правилом буравчика (рис. 9.10.a). В противном случае циркуляция отрицательна (рис. 9.10.b).

Рис. 9.10.

Если магнитное поле создаётся не одним, а несколькими токами, то циркуляция такого поля по замкнутому контуру будет пропорциональна алгебраической сумме токов, охватываемыхэтим контуром:

. (9.16)

Для случая, представленного на рис. 9.11.:

.

При выбранном направлении обхода контура (по часовой стрелке — на рис. 9.11.) знак тока определяется правилом буравчика. Токи I₁иI₅не вошли в сумму токов, так как они оказались вне замкнутого контура.

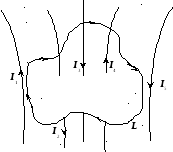
Рис. 9.11.

Подводя итог, сформулируем теорему о циркуляции магнитного поля: циркуляция вектора магнитной индукции по замкнутому контуру пропорциональна алгебраической сумме токов, охватываемых этим контуром.

Здесь заканчивается важный этап нашей работы: мы записали последнее уравнение системы уравнений Максвелла для электро- и магнитостатики. Вот эти уравнения:

,	(I)	,	(III)
,	(II)	.	(IV)

Система включает два уравнения потока (IиIII) и два уравнения циркуляции (IIиIV) для электростатических и магнитных полей.

Повторим физическое содержание этих уравнений:

I —	источником электростатического поля являются электрические заряды;
II —	электростатическое поле потенциально;
III —	в природе отсутствуют магнитные заряды;
IV —	источником магнитного поля является электрический ток.