
- •Курс общей физики (лекции)
- •Электродинамика и научно-технический прогресс
- •Свойства электрических зарядов
- •Закон Кулона
- •Электрическое поле
- •Идеи близко - и дальнодействия
- •Напряжённость электрического поля. Поле точечного заряда. Графическое представление электрических полей
- •Принцип суперпозиции электрических полей
- •Поле диполя
- •Поле бесконечно заряженной нити
- •Лекция 2«Теорема Гаусса для электрического поля»
- •Поток вектора напряжённости электрического поля
- •Теорема Гаусса для электрического поля
- •Применение теоремы Гаусса для расчёта электрических полей
- •Поле бесконечной заряженной нити
- •Поле бесконечной равномерно заряженной плоскости. Поле плоского конденсатора
- •Поле сферического конденсатора
- •Лекция 3 «Потенциал электростатического поля»
- •Работа сил электростатического поля при перемещении заряда. Потенциал и разность потенциалов.
- •Теорема о циркуляции в вектора напряжённости электростатического поля
- •Связь напряжённости и потенциала электростатического поля
- •Примеры расчёта потенциала электростатических полей
- •Потенциал поля точечного заряда (рис. 3.8.)
- •Разность потенциалов на обкладках сферического конденсатора (рис. 3.9.)
- •Лекция 4 «Электростатика проводников»
- •Электрическое поле заряженного проводника
- •Проводники во внешнем электрическом поле. Явление электростатической индукции. Электрическая защита.
- •Электроёмкость проводника. Конденсаторы. Емкость конденсаторов.
- •Ёмкость плоского конденсатора
- •Ёмкость сферического конденсатора
- •Ёмкость цилиндрического конденсатора
- •Энергия электрического поля. Плотность энергии.
- •Лекция 5 «Электрическое поле в диэлектриках»
- •Типы диэлектриков. Поляризация диэлектриков. Поляризуемость и вектор поляризации.
- •Диэлектрическая проницаемость. Вектор электрического смещения.
- •Законы электрического поля в диэлектриках
- •Закон Кулона
- •Теорема Остроградского-Гаусса
- •Условия на границе двух диэлектриков
- •Лекция 6 «Постоянный электрический ток»
- •Электрический ток. Характеристики электрического тока
- •Законы Ома для участка цепи
- •Закон Ома в интегральной форме
- •Закон Ома в дифференциальной форме
- •Пример расчёта силы тока в проводящей среде
- •Закон Джоуля-Ленца в интегральной и дифференциальной формах
- •Лекция 7 «Постоянный электрический ток»
- •Сторонние силы. Источники тока. Э.Д.С. Источника
- •Закон Ома для неоднородного участка цепи. Закон Ома для замкнутого контура.
- •Правила Кирхгофа
- •Классическая теория электропроводности металлов
- •Лекция 8 «Электромагнетизм. Основы магнитостатики»
- •Электростатика. Краткий обзор.
- •Магнитное взаимодействие электрических токов
- •Магнитное поле. Закон Ампера. Индукция магнитного поля.
- •Принцип суперпозиции магнитных полей. Закон Био-Савара-Лапласа.
- •Магнитное поле прямолинейного тока
- •Магнитное поле на оси кругового тока
- •Магнитное поле движущегося заряда
- •Лекция 9 «Основы магнитостатики»
- •Краткий обзор предыдущей лекции
- •Сила Лоренца
- •Теорема Гаусса и теорема о циркуляции магнитного поля. Система уравнений Максвелла электро- и магнитостатики.
- •Примеры расчёта магнитных полей
- •Поле прямолинейного тока
- •Поле бесконечного соленоида
- •Поле тороида
- •Лекция 10 «Электромагнитная индукция. Энергия магнитного поля»
- •Явление электромагнитной индукции
- •Опыты Фарадея
- •Правило Ленца
- •Электродвижущая сила индукции. Закон Фарадея.
- •Индуктивность. Индуктивность соленоида. Явление самоиндукции.
- •Токи размыкания и замыкания цепи. Энергия и плотность энергии магнитного поля.
- •Лекция 11 «Электрические колебания»
- •Колебательные контуры. Квазистационарные токи.
- •Собственные электрические колебания
- •Собственные незатухающие колебания
- •Собственные затухающие колебания
- •Вынужденные колебания
- •Резистор (r) в цепи переменного тока (рис. 11.7.)
- •Индуктивность в цепи переменного тока (рис. 11.9.)
- •Вынужденные колебания. Резонанс.
- •Проблема косинуса фи
- •Лекция 12 «Теория Максвелла»
- •Две трактовки явления электромагнитной индукции. Вихревое электрическое поле
- •Ток смещения. Обобщение теоремы о циркуляции магнитного поля
- •Полная система уравнений Максвелла и их физический смысл
- •Лекция 13 «Электромагнитные волны»
- •Волновой процесс. Уравнение плоской волны. Волновое уравнение.
- •Плоская электромагнитная волна. Свойства электромагнитных волн.
- •Энергия электромагнитных волн. Плотность потока энергии. Вектор Пойнтинга.
- •Примеры вычисления плотности потока энергии
- •Плотность потока энергии в плоской электромагнитной волне в вакууме
- •Плотность потока энергии электромагнитного поля в цепи постоянного тока. Выделение джоулева тепла в проводнике.
- •Лекция 14 «Магнетизм как релятивистский эффект»
- •Магнитная сила как релятивистское следствие закона Кулона
- •Релятивистское преобразование магнитных и электрических полей
- •Пример 1
- •Пример 2
- •Рекомендуемая литература
- •Содержание
Поле сферического конденсатора
Обкладками сферического конденсатора являются две концентрические сферы (R1иR2). Сообщим этим поверхностям одинаковые по величине, но разноимённые заряды+qи–qи вычислим электрическое поле, создаваемое этими зарядами в пространстве (рис. 2.10.).
Сферы делят пространство на 3 области:
I— внутри первой сферы (r1<R1),
II— между обкладками (R1r2<R2),
III— за пределами конденсатора (r3>R2).
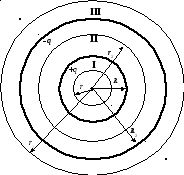
Рис. 2.10.
Область I.
Выберем замкнутую гауссову поверхность внутри первой области. Разумно, руководствуясь соображениями симметрии, эту поверхность выбрать сферической (r1).
Поток вектора напряжённости через эту поверхность (по определению потока) равен:
![]()
Этот поток, согласно теореме Гаусса, пропорционален заряду, заключённому внутри поверхности. Но внутри сферы радиуса r1заряд отсутствует. Поэтому и поток равен нулю
![]() (!)
(!)
Отсюда заключаем, что в области Iполе равно нулю
0 < r<R1,E= 0 (2.18)
Область II.
Вновь в качестве замкнутой поверхности выберем сферу, но теперь её радиус r2лежит в пределах отR1доR2.
Вычислим поток вектора напряжённости поля через эту гауссову поверхность.
![]()
Воспользуемся теорией Гаусса:
![]() :
:
![]()
Оказывается, что электрическое поле между обкладками сферического конденсатора неотличимо от поля точечного заряда
![]() . (2.19)
. (2.19)
Посмотрим теперь, как выглядит поле в области III.
Вновь выберем замкнутую гауссову сферическую поверхность (радиус r3>R2). Вычисляем поток вектора напряжённости
![]()
Этот поток равен нулю, так как он пропорционален алгебраической сумме зарядов, заключённых внутри этой поверхности. Но алгебраическая сумма одинаковых разноимённых зарядов равна нулю
![]()
Отсюда следует, что Е = 0 (r3R2)/
График Е=Е(r) приведён на рисунке 2.11.

Рис. 2.11.
Лекция 3 «Потенциал электростатического поля»
План лекции
3.1. Работа сил электростатического поля при перемещении заряда. Потенциал и разность потенциалов.
3.2. Теорема о циркуляции вектора напряжённости электростатического поля.
3.3. Связь напряжённости и потенциала электростатического поля.
3.4. Примеры расчёта потенциала электростатического поля.
3.4.1. Потенциал поля точечного заряда.
3.4.2. Разность потенциалов на обкладках сферического конденсатора.
Существуют две характеристики электрического поля. В любой точке пространства поле можно задать либо вектором напряжённости — это «силовая» характеристика поля, либо потенциалом — это его энергетическая характеристика.
Потенциал — энергетическая характеристика поля, связанная и с энергией заряда в электростатическом поле и с работой, совершаемой электрической силой при перемещении заряда.
Работа сил электростатического поля при перемещении заряда. Потенциал и разность потенциалов.
Рассмотрим произвольное перемещение (1–а–2) зарядаqв электростатическом поле. Пусть поле создаётся неподвижным точечным зарядомQ(рис. 3.1.). В процессе перемещения на зарядq действует кулоновская сила:
![]() . (3.1)
. (3.1)

Рис. 3.1.
Её работа на перемещении
![]() равна:
равна:
![]() . (3.2)
. (3.2)
Здесь dr=dlсos— толщина сферической оболочки, окружающей зарядQ. Полная работа электрической силы равна сумме работ на всех участках траектории:
![]() . (3.3)
. (3.3)
Теперь несложно показать, что эта работа
не зависит от формы траектории и остаётся
неизменной, если начальная и конечная
точки траектории не меняют своего
положения. Рассмотрим, например,
перемещение того же заряда q
из начальной точки 1 в конечную 2 по
новой траектории 1–b–2.
При преодолении прежнего сферического
слоя на перемещении![]() электрическая сила совершит работу:
электрическая сила совершит работу:
![]() . (3.4)
. (3.4)
Но ведь эта работа в точности совпадает с работой на перемещении dl(3.2) по первоначальной траектории 1–а–2.
Полная работа, равная сумме элементарных работ на всех участках новой траектории, будет равна работе электрической силы на траектории 1–а–2:
![]() . (3.5)
. (3.5)
Вспомним, что силы, работа которых не зависит от вида траектории и определяется только положением её начальной и конечной точек, называются консервативными.
Мы пришли к выводу, что кулоновская сила консервативна. Впрочем, ничего неожиданного в этом выводе нет: ведь сила взаимодействия двух точечных зарядов может быть отнесена к классу центральных сил, а все центральные силы, как было установлено в механике, консервативны.
Итак, вычислим работу кулоновской силы при перемещении заряда qиз точки 1 в положение 2 (по любой траектории):
 (3.6)
(3.6)
Как и следовало ожидать, величина работы никак не связана с видом траектории. Она зависит только от положения её начальной (r1) и конечной (r2) точек.
В механике было показано, что работа консервативной силы равна убыли потенциальной энергии системы:
![]() . (3.7)
. (3.7)
Присмотримся внимательнее к результату (3.6):
![]() .
.
Сопоставив этот результат с теоремой о работе консервативной силы (3.7), запишем уравнение:
![]() ,
,
из которого следует, что потенциальная энергия системы:
![]() +const. (3.9)
+const. (3.9)
Это потенциальная энергия системы двух точечных зарядов, или, что то же самое, энергия заряда qв электрическом поле точечного зарядаQ.
Константа в выражении (3.9) принимается
обычно равной нулю. Это означает, что
принимается равной нулю энергия
взаимодействия зарядов qиQна бесконечном удалении
их друг от друга (приr= ∞).Тогда на расстоянииrэнергия взаимодействия равна![]() . (3.10)
. (3.10)
Потенциальная энергия заряженной частицы в электрическом поле зависит, таким образом, от величины заряда qи от его положения в поле относительно зарядаQ, создающего поле.
Энергия единичного (q= 1) точечного заряда уже не будет связана с величиной этого пробного зарядаqи может быть принята в качестве энергетической характеристики данной точки электростатического поля:
![]() .
.
Эта энергетическая характеристика поля получила название потенциал — .
Потенциал произвольной точки электростатического поля равен энергии единичного положительного заряда, помещённого в эту точку.
Можно придать потенциалу и иной физический смысл.
Поместим заряд qв поле точечного зарядаQ. Первоначально расстояние между зарядами —r. Отпустим зарядq. Под действием электрической силы отталкивания зарядqудалится в бесконечность (рис. 3.2.). На этом перемещении кулоновская сила совершит работу:
![]() . (3.11)
. (3.11)
Эта работа не зависит от формы траектории, поэтому мы её вычислили, считая, что заряд qудаляется по радиусу.

Рис. 3.2.
Сравнивая (3.10) и (3.11), заключаем, что:
![]() . (3.12)
. (3.12)
Потенциал некоторой точки электростатического поля равен работе, совершаемой электрической силой при эвакуации единичного положительного заряда из этой точки в бесконечность.
Теперь вычислим потенциал поля, созданного системой точечных зарядов Q1,Q2, …,QN.
При перемещении заряда qиз точки 1 в бесконечность электрическая сила совершит работу, равную алгебраической сумме работ сил, действующих на движущийся заряд со стороны зарядовQ1,Q2, …,QN(рис. 3.3.):
![]()

Рис. 3.3.
Согласно (3.12) работа каждой силы равна:
![]() . (3.13)
. (3.13)
Здесь
![]() — потенциал поля, создаваемого в точке
1 зарядомQi.
— потенциал поля, создаваемого в точке
1 зарядомQi.
Таким образом, суммарная работа равна:
![]() ,
,
где
![]() .
.
Потенциал поля, созданного системой точечных зарядов, равен алгебраической сумме потенциалов, создаваемых в рассматриваемой точке каждым из зарядов в отдельности:
![]() . (3.14)
. (3.14)
Результат (3.14) известен как «принцип суперпозиции для потенциала». Это очень важный вывод, позволяющий использовать понятие потенциала не только для характеристики полей точечных зарядов, но и для любых произвольных электростатических полей.
Ещё раз обратимся к вычислению работы электрической силы при перемещении заряда qиз точки 1 теперь уже произвольного электростатического поля в бесконечность. Поскольку эта работа не зависит от формы траектории, унося заряд в бесконечность, пройдём предварительно точку 2 электростатического поля (рис. 3.4.).

Рис. 3.4.
Ясно, что вся работа на этом перемещении складывается из двух частей:
![]() .
.
Разделив это равенство на величину переносимого заряда q, получим:
![]() ,
,
или:
![]() . (3.15)
. (3.15)
Здесь
![]() —разность потенциаловдвух точек
поля. Она равна работе, совершаемой
электрической силой при перемещении
единичного заряда из первой точки во
вторую:
—разность потенциаловдвух точек
поля. Она равна работе, совершаемой
электрической силой при перемещении
единичного заряда из первой точки во
вторую:
![]() . (3.16)
. (3.16)
Таким образом, зная разность потенциалов двух точек поля, легко вычислить работу электрического поля, совершаемую при перемещении заряда qмежду этими точками:
![]() . (3.17)
. (3.17)
В международной системе единиц СИ потенциал (и разность потенциалов) измеряется в вольтах:

![]() .
.
Разность потенциалов двух точек электростатического поля равна одному вольту, если при переносе заряда q= 1Кл между этими точками, электрическая сила совершает работуА(Fэл.) = 1 Дж.
