
- •Курс общей физики (лекции)
- •Электродинамика и научно-технический прогресс
- •Свойства электрических зарядов
- •Закон Кулона
- •Электрическое поле
- •Идеи близко - и дальнодействия
- •Напряжённость электрического поля. Поле точечного заряда. Графическое представление электрических полей
- •Принцип суперпозиции электрических полей
- •Поле диполя
- •Поле бесконечно заряженной нити
- •Лекция 2«Теорема Гаусса для электрического поля»
- •Поток вектора напряжённости электрического поля
- •Теорема Гаусса для электрического поля
- •Применение теоремы Гаусса для расчёта электрических полей
- •Поле бесконечной заряженной нити
- •Поле бесконечной равномерно заряженной плоскости. Поле плоского конденсатора
- •Поле сферического конденсатора
- •Лекция 3 «Потенциал электростатического поля»
- •Работа сил электростатического поля при перемещении заряда. Потенциал и разность потенциалов.
- •Теорема о циркуляции в вектора напряжённости электростатического поля
- •Связь напряжённости и потенциала электростатического поля
- •Примеры расчёта потенциала электростатических полей
- •Потенциал поля точечного заряда (рис. 3.8.)
- •Разность потенциалов на обкладках сферического конденсатора (рис. 3.9.)
- •Лекция 4 «Электростатика проводников»
- •Электрическое поле заряженного проводника
- •Проводники во внешнем электрическом поле. Явление электростатической индукции. Электрическая защита.
- •Электроёмкость проводника. Конденсаторы. Емкость конденсаторов.
- •Ёмкость плоского конденсатора
- •Ёмкость сферического конденсатора
- •Ёмкость цилиндрического конденсатора
- •Энергия электрического поля. Плотность энергии.
- •Лекция 5 «Электрическое поле в диэлектриках»
- •Типы диэлектриков. Поляризация диэлектриков. Поляризуемость и вектор поляризации.
- •Диэлектрическая проницаемость. Вектор электрического смещения.
- •Законы электрического поля в диэлектриках
- •Закон Кулона
- •Теорема Остроградского-Гаусса
- •Условия на границе двух диэлектриков
- •Лекция 6 «Постоянный электрический ток»
- •Электрический ток. Характеристики электрического тока
- •Законы Ома для участка цепи
- •Закон Ома в интегральной форме
- •Закон Ома в дифференциальной форме
- •Пример расчёта силы тока в проводящей среде
- •Закон Джоуля-Ленца в интегральной и дифференциальной формах
- •Лекция 7 «Постоянный электрический ток»
- •Сторонние силы. Источники тока. Э.Д.С. Источника
- •Закон Ома для неоднородного участка цепи. Закон Ома для замкнутого контура.
- •Правила Кирхгофа
- •Классическая теория электропроводности металлов
- •Лекция 8 «Электромагнетизм. Основы магнитостатики»
- •Электростатика. Краткий обзор.
- •Магнитное взаимодействие электрических токов
- •Магнитное поле. Закон Ампера. Индукция магнитного поля.
- •Принцип суперпозиции магнитных полей. Закон Био-Савара-Лапласа.
- •Магнитное поле прямолинейного тока
- •Магнитное поле на оси кругового тока
- •Магнитное поле движущегося заряда
- •Лекция 9 «Основы магнитостатики»
- •Краткий обзор предыдущей лекции
- •Сила Лоренца
- •Теорема Гаусса и теорема о циркуляции магнитного поля. Система уравнений Максвелла электро- и магнитостатики.
- •Примеры расчёта магнитных полей
- •Поле прямолинейного тока
- •Поле бесконечного соленоида
- •Поле тороида
- •Лекция 10 «Электромагнитная индукция. Энергия магнитного поля»
- •Явление электромагнитной индукции
- •Опыты Фарадея
- •Правило Ленца
- •Электродвижущая сила индукции. Закон Фарадея.
- •Индуктивность. Индуктивность соленоида. Явление самоиндукции.
- •Токи размыкания и замыкания цепи. Энергия и плотность энергии магнитного поля.
- •Лекция 11 «Электрические колебания»
- •Колебательные контуры. Квазистационарные токи.
- •Собственные электрические колебания
- •Собственные незатухающие колебания
- •Собственные затухающие колебания
- •Вынужденные колебания
- •Резистор (r) в цепи переменного тока (рис. 11.7.)
- •Индуктивность в цепи переменного тока (рис. 11.9.)
- •Вынужденные колебания. Резонанс.
- •Проблема косинуса фи
- •Лекция 12 «Теория Максвелла»
- •Две трактовки явления электромагнитной индукции. Вихревое электрическое поле
- •Ток смещения. Обобщение теоремы о циркуляции магнитного поля
- •Полная система уравнений Максвелла и их физический смысл
- •Лекция 13 «Электромагнитные волны»
- •Волновой процесс. Уравнение плоской волны. Волновое уравнение.
- •Плоская электромагнитная волна. Свойства электромагнитных волн.
- •Энергия электромагнитных волн. Плотность потока энергии. Вектор Пойнтинга.
- •Примеры вычисления плотности потока энергии
- •Плотность потока энергии в плоской электромагнитной волне в вакууме
- •Плотность потока энергии электромагнитного поля в цепи постоянного тока. Выделение джоулева тепла в проводнике.
- •Лекция 14 «Магнетизм как релятивистский эффект»
- •Магнитная сила как релятивистское следствие закона Кулона
- •Релятивистское преобразование магнитных и электрических полей
- •Пример 1
- •Пример 2
- •Рекомендуемая литература
- •Содержание
Принцип суперпозиции электрических полей
Известна сила
![]() ,
с которой взаимодействуют два точечных
зарядаQ1иq(рис. 1.8.).Опыт свидетельствуето
том, что эта сила не изменится, если
рядом появятся другие точечные зарядыQ2…Qi…QN
(рис. 1.9.)
,
с которой взаимодействуют два точечных
зарядаQ1иq(рис. 1.8.).Опыт свидетельствуето
том, что эта сила не изменится, если
рядом появятся другие точечные зарядыQ2…Qi…QN
(рис. 1.9.)

Рис. 1.8.

Рис. 1.9.
Результирующая сила, действующая на заряд q,будет равна в этом случае векторной сумме отдельных сил
![]() (1.4)
(1.4)
Разделив (1.4) на величину заряда q, мы придём к важному выводу:
![]()
Если поле в некоторой точке пространства
создаётся отдельными точечными зарядами,
то напряжённость результирующего поля
![]() равна векторной сумме напряженностей
складываемых полей
равна векторной сумме напряженностей
складываемых полей
![]() (1.5)
(1.5)
Это правило получило название принципа суперпозиции электрических полей. Подчеркнем ещё раз, что справедливость этого принципа подтверждена экспериментально.
Принцип суперпозиции позволяет вычислить поля, созданные различными комбинациями зарядов.
Поле диполя
Диполемназывается система двух
точечных одинаковых по величине и
противоположных по знаку зарядов (рис.
1.10.). Расстояние между зарядамиlназываетсяплечом диполя. Плечу
приписывается направление по оси диполя
от отрицательного заряда к положительному.
Вектор![]() называетсяэлектрическим моментом
диполя.
называетсяэлектрическим моментом
диполя.
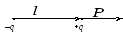
Рис. 1.10.
Воспользовавшись принципом суперпозиции электрических полей, вычислим поле на оси диполя в точке А, отстоящей от центра диполя на расстоянииrl(рис. 1.11.). Электрическое поле в рассматриваемой точке возникает как результат сложения двух полей, созданных точечными зарядами +qи –q.
![]()
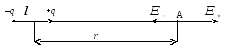
Рис. 1.11.
Спроецируем это уравнение на ось диполя и воспользуемся уравнением (1.3) для напряжённости поля точечного заряда
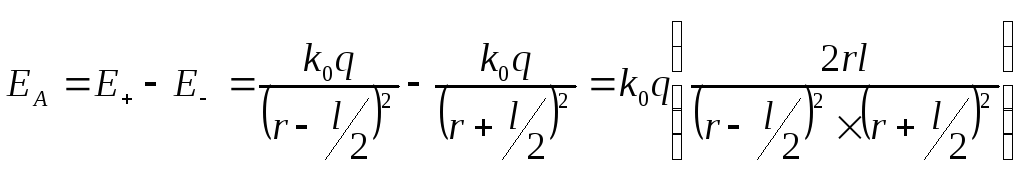
Учитывая, что
![]() <<r, окончательный
результат запишем так
<<r, окончательный
результат запишем так
![]() (1.6)
(1.6)
Здесь важно отметить три момента:
Напряжённость поля ЕАна оси диполя пропорциональна его электрическому моментуР.
Поле диполя убывает с расстоянием rбыстрее, чем поле точечного заряда —обратно пропорциональнокубурасстояния.
Напряжённость поля на оси диполя ЕАсовпадает по направлению с направлением плеча диполя
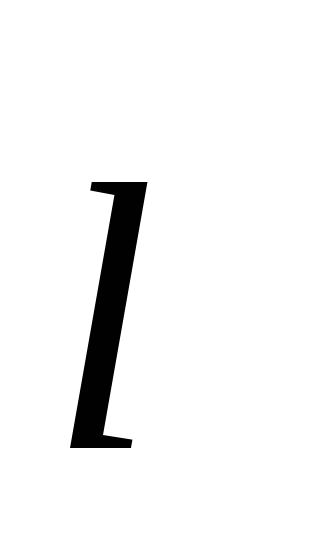 и его электрического момента
и его электрического момента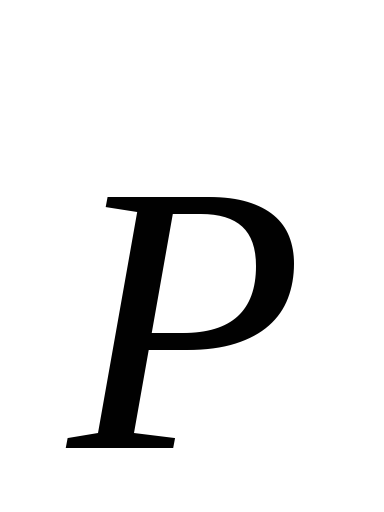 .
.
Поле бесконечно заряженной нити
Рассмотрим бесконечную нить, несущую заряд, равномерно распределённый по её длине. Заряд, сосредоточенный на бесконечно нити, конечно, тоже бесконечен, и поэтому он не может служить количественной характеристикой степени заряженности нити. В качестве такой характеристики принимается «линейная плотность заряда». Эта величина равна заряду, распределённому на отрезке нити единичной длины:
![]() .
.
Выясним, какова напряженность поля, создаваемого заряженной нитью на расстоянии а от неё (рис. 1.12).
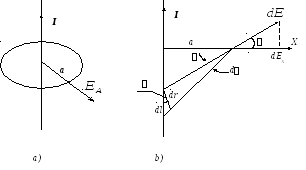
Рис. 1.12.
Для вычисления напряжённости вновь воспользуемся принципом суперпозиции электрических полей и законом Кулона. Выберем на нити элементарный участок dl.На этом участке сосредоточен зарядdq=dl, который можно считать точечным. В точке А такой заряд создаёт поле (см. 1.3)
![]()
Исходя из симметрии задачи, можно
заключить, что искомый вектор напряжённости
поля
![]() будет направлен по линии, перпендикулярной
нити, то есть вдоль осих. Поэтому
сложение векторов напряжённости, можно
заменить сложением их проекцией на это
направление.
будет направлен по линии, перпендикулярной
нити, то есть вдоль осих. Поэтому
сложение векторов напряжённости, можно
заменить сложением их проекцией на это
направление.
![]() (1.7)
(1.7)
Рис. (1.12 b) позволяет сделать следующие заключения:
 (1.8)
(1.8)
Таким образом
![]() . (1.9)
. (1.9)
Используя (1.8) и (1.9) в уравнении (1.7), получим
![]() (1.10)
(1.10)
Теперь для решения задачи осталось
проинтегрировать (1.10) по всей длине
нити. Это означает, что угол будет меняться от![]() до
до![]() .
.
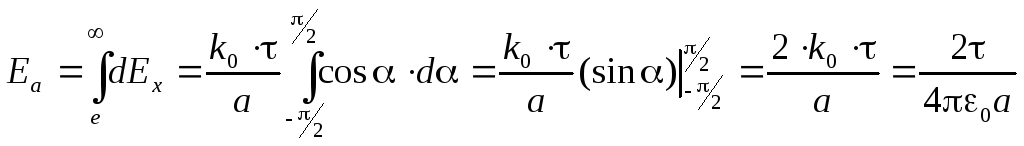 (1.11)
(1.11)
В этой задаче поле обладает цилиндрической симметрией. Напряжённость поля прямо пропорциональна линейной плотности заряда на нити и обратно пропорциональна расстояниюаот нити до той точки, где измеряется напряжённость.
