
- •Курс общей физики (лекции)
- •Электродинамика и научно-технический прогресс
- •Свойства электрических зарядов
- •Закон Кулона
- •Электрическое поле
- •Идеи близко - и дальнодействия
- •Напряжённость электрического поля. Поле точечного заряда. Графическое представление электрических полей
- •Принцип суперпозиции электрических полей
- •Поле диполя
- •Поле бесконечно заряженной нити
- •Лекция 2«Теорема Гаусса для электрического поля»
- •Поток вектора напряжённости электрического поля
- •Теорема Гаусса для электрического поля
- •Применение теоремы Гаусса для расчёта электрических полей
- •Поле бесконечной заряженной нити
- •Поле бесконечной равномерно заряженной плоскости. Поле плоского конденсатора
- •Поле сферического конденсатора
- •Лекция 3 «Потенциал электростатического поля»
- •Работа сил электростатического поля при перемещении заряда. Потенциал и разность потенциалов.
- •Теорема о циркуляции в вектора напряжённости электростатического поля
- •Связь напряжённости и потенциала электростатического поля
- •Примеры расчёта потенциала электростатических полей
- •Потенциал поля точечного заряда (рис. 3.8.)
- •Разность потенциалов на обкладках сферического конденсатора (рис. 3.9.)
- •Лекция 4 «Электростатика проводников»
- •Электрическое поле заряженного проводника
- •Проводники во внешнем электрическом поле. Явление электростатической индукции. Электрическая защита.
- •Электроёмкость проводника. Конденсаторы. Емкость конденсаторов.
- •Ёмкость плоского конденсатора
- •Ёмкость сферического конденсатора
- •Ёмкость цилиндрического конденсатора
- •Энергия электрического поля. Плотность энергии.
- •Лекция 5 «Электрическое поле в диэлектриках»
- •Типы диэлектриков. Поляризация диэлектриков. Поляризуемость и вектор поляризации.
- •Диэлектрическая проницаемость. Вектор электрического смещения.
- •Законы электрического поля в диэлектриках
- •Закон Кулона
- •Теорема Остроградского-Гаусса
- •Условия на границе двух диэлектриков
- •Лекция 6 «Постоянный электрический ток»
- •Электрический ток. Характеристики электрического тока
- •Законы Ома для участка цепи
- •Закон Ома в интегральной форме
- •Закон Ома в дифференциальной форме
- •Пример расчёта силы тока в проводящей среде
- •Закон Джоуля-Ленца в интегральной и дифференциальной формах
- •Лекция 7 «Постоянный электрический ток»
- •Сторонние силы. Источники тока. Э.Д.С. Источника
- •Закон Ома для неоднородного участка цепи. Закон Ома для замкнутого контура.
- •Правила Кирхгофа
- •Классическая теория электропроводности металлов
- •Лекция 8 «Электромагнетизм. Основы магнитостатики»
- •Электростатика. Краткий обзор.
- •Магнитное взаимодействие электрических токов
- •Магнитное поле. Закон Ампера. Индукция магнитного поля.
- •Принцип суперпозиции магнитных полей. Закон Био-Савара-Лапласа.
- •Магнитное поле прямолинейного тока
- •Магнитное поле на оси кругового тока
- •Магнитное поле движущегося заряда
- •Лекция 9 «Основы магнитостатики»
- •Краткий обзор предыдущей лекции
- •Сила Лоренца
- •Теорема Гаусса и теорема о циркуляции магнитного поля. Система уравнений Максвелла электро- и магнитостатики.
- •Примеры расчёта магнитных полей
- •Поле прямолинейного тока
- •Поле бесконечного соленоида
- •Поле тороида
- •Лекция 10 «Электромагнитная индукция. Энергия магнитного поля»
- •Явление электромагнитной индукции
- •Опыты Фарадея
- •Правило Ленца
- •Электродвижущая сила индукции. Закон Фарадея.
- •Индуктивность. Индуктивность соленоида. Явление самоиндукции.
- •Токи размыкания и замыкания цепи. Энергия и плотность энергии магнитного поля.
- •Лекция 11 «Электрические колебания»
- •Колебательные контуры. Квазистационарные токи.
- •Собственные электрические колебания
- •Собственные незатухающие колебания
- •Собственные затухающие колебания
- •Вынужденные колебания
- •Резистор (r) в цепи переменного тока (рис. 11.7.)
- •Индуктивность в цепи переменного тока (рис. 11.9.)
- •Вынужденные колебания. Резонанс.
- •Проблема косинуса фи
- •Лекция 12 «Теория Максвелла»
- •Две трактовки явления электромагнитной индукции. Вихревое электрическое поле
- •Ток смещения. Обобщение теоремы о циркуляции магнитного поля
- •Полная система уравнений Максвелла и их физический смысл
- •Лекция 13 «Электромагнитные волны»
- •Волновой процесс. Уравнение плоской волны. Волновое уравнение.
- •Плоская электромагнитная волна. Свойства электромагнитных волн.
- •Энергия электромагнитных волн. Плотность потока энергии. Вектор Пойнтинга.
- •Примеры вычисления плотности потока энергии
- •Плотность потока энергии в плоской электромагнитной волне в вакууме
- •Плотность потока энергии электромагнитного поля в цепи постоянного тока. Выделение джоулева тепла в проводнике.
- •Лекция 14 «Магнетизм как релятивистский эффект»
- •Магнитная сила как релятивистское следствие закона Кулона
- •Релятивистское преобразование магнитных и электрических полей
- •Пример 1
- •Пример 2
- •Рекомендуемая литература
- •Содержание
Энергия электромагнитных волн. Плотность потока энергии. Вектор Пойнтинга.
Разумно предположить, что энергия электромагнитной волны складывается из энергии электрического поля волны и магнитного. Тогда энергия единицы объема — объемная плотность энергии — может быть представлена такой суммой (см. 4.14 и 10.11):
= E
+H=
![]() . (13.11)
. (13.11)
Учитывая, что
![]() плотность энергии электромагнитной
волны можно записать еще и так:
плотность энергии электромагнитной
волны можно записать еще и так:
=
![]() (13.12)
(13.12)
По мере распространения волны, все новые
и новые области пространства вовлекаются
в волновой процесс. В эти области от
источника волна приносит энергию.
Выделим в пространстве площадку Sи вычислим энергию, которая за времяпроходит с волной через эту площадку
(рис. 13.4.). Построим наSпараллелепипед, ребра которого параллельны
скорости распространения волны![]() .
Длина ребер равна произведениюv.
Тогда за времячерез площадкуSпройдет с волной вся энергия, сосредоточенная
в объеме этого параллелепипеда.
.
Длина ребер равна произведениюv.
Тогда за времячерез площадкуSпройдет с волной вся энергия, сосредоточенная
в объеме этого параллелепипеда.
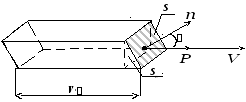
Рис. 13.4.
W
=V
=
S![]() S
S![]() EHS
EHS![]()
Здесь мы учли, что
![]() иSn=Scos— площадь нормального сечения
параллелепипеда.
иSn=Scos— площадь нормального сечения
параллелепипеда.
Ежесекундно через поверхность единичной площади, перпендикулярную направлению распространения волны, проходит энергия
![]() (13.13)
(13.13)
Этот результат принято записывать в виде векторного произведения
![]() . (13.14)
. (13.14)
Вектор
![]() называется вектором Пойнтинга. Его
направление совпадает с направлением
вектора фазовой скорости.Численно
вектор Пойнтинга равен плотности потока
энергии, то есть той энергии, которая в
единицу времени протекает через единичную
площадку, перпендикулярную направлению
скорости распространения волны.
Напомним, что в электромагнитной волне
направления векторов
называется вектором Пойнтинга. Его
направление совпадает с направлением
вектора фазовой скорости.Численно
вектор Пойнтинга равен плотности потока
энергии, то есть той энергии, которая в
единицу времени протекает через единичную
площадку, перпендикулярную направлению
скорости распространения волны.
Напомним, что в электромагнитной волне
направления векторов![]() и
и![]() связаны правилом правого винта.
связаны правилом правого винта.
Примеры вычисления плотности потока энергии
Рассмотрим два примера расчета потока электромагнитной энергии.
Плотность потока энергии в плоской электромагнитной волне в вакууме
Пусть волна распространяется в положительном направлении оси x:
E = E0cos(t – kx)
H = H0cos(t – kx).
(Колебания EиHсинфазны и, кроме того,![]() ).
).
Тогда мгновенное значение плотности потока энергии
P = E0H0 cos2(t – kx)
Среднее значение модуля вектора Пойнтига мы получим, усреднив квадрат косинуса:
![]()
Учитывая, что
![]() этому результату можно придать такой
вид:
этому результату можно придать такой
вид:
![]()
Средняя плотность потока энергии
(интенсивность) электромагнитной
волны пропорциональна квадрату амплитуды
колебания вектора![]() или вектора
или вектора![]()
Плотность потока энергии электромагнитного поля в цепи постоянного тока. Выделение джоулева тепла в проводнике.
По цилиндрическому проводнику радиуса
rтечет постоянный
ток с плотностью![]() .
.
На поверхности проводника напряженности электрического и магнитного полей направлены так, как показано на рис. 13.5. Их модули соответственно равны
![]() (закон Ома) и
(закон Ома) и
![]() (теорема о циркуляции вектора
(теорема о циркуляции вектора![]() ).
).
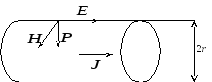
Рис. 13.5.
Плотность потока энергии
![]()
Вектор Пойнтинга направлен от поверхности внутрь проводника (рис. 13.5.).
В единицу времени внутрь проводника длины lчерез его боковую поверхность втечет энергия
![]() .
.
Вспомним, что
![]() — это джоулево тепло, выделяющееся в
единичном объеме проводника ежесекундно
(закон Джоуля-Ленца в дифференциальной
форме), а
— это джоулево тепло, выделяющееся в
единичном объеме проводника ежесекундно
(закон Джоуля-Ленца в дифференциальной
форме), а![]() — объем участка проводника. Следовательно
— объем участка проводника. Следовательно![]() — джоулево тепло, выделяющееся за
единицу времени на участкеlпроводника!
— джоулево тепло, выделяющееся за
единицу времени на участкеlпроводника!
Наш расчет привел к неожиданному результату: тепло, выделяющееся в проводнике, есть электромагнитная энергия, втекающая в проводник через его поверхность, а не перемещается вдоль его оси вместе с носителями заряда, как это могло бы показаться на первый взгляд.
