2. Магнитное поле. Закон Ампера. Индукция магнитного поля.

В электростатике на этом этапе вводится основная характеристика электрического поля — вектор напряжённости (Э2).

Подобный шаг нам предстоит сделать и сейчас: ввести основную характеристику магнитного поля — вектор магнитной индукции .

Магнитное поле не действует на неподвижные заряды. В магнитном поле сила действует на электрический ток.

Согласно закону Ампера, максимальнаясилаdF_max, действующая на участок проводникаdlс токомI, пропорциональна произведениюIdl(рис. 8.4.):

dF_max=BIdl. (8.2)

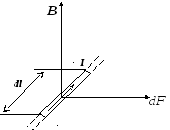
Рис. 8.4.

Коэффициент пропорциональности В— модуль вектора магнитной индукции поля:

.

Направление вектора магнитной индукции определяется по правилу левой руки: руку располагают так, чтобы четыре пальца были направлены по току в проводнике, а отставленный большой палец — по направлению силы, действующей со стороны магнитного поля на ток. При этом вектор магнитной индукции направлен в ладонь.

Напряжённость электрическогополя определялась как сила, действующая в поле наединичныйположительныйзаряд.

Модуль вектора магнитнойиндукции равен максимальной силе, действующей наединичный элемент тока. Под элементом тока подразумевается произведение.

Окончательно представим закон Ампера в векторном виде:

. (8.3)

Сила Ампера , действующая в магнитном поле, пропорциональна векторному произведению.

Здесь — вектор, равный длине участкаdlи направленный по току. В соответствии с правилом векторного произведения, сила Ампераперпендикулярна плоскости, содержащей перемножаемые векторыи. Это означает, что сила, действующая в магнитном полена элемент тока, перпендикулярна и вектору магнитной индукциии элементу тока.

Единица измерения вектора магнитной индукции называется тесла (Тл):

.

В этом ряду приведены различные, часто встречающиеся наименования единицы магнитной индукции.

В заключение напомним, что при определении направления силы Ампера (7.3), можно не только руководствоваться свойством векторного произведения, но и использовать правило «винта» («буравчика») и правило «левой руки».

3. Принцип суперпозиции магнитных полей. Закон Био-Савара-Лапласа.

Опыт, как уже отмечалось, свидетельствует о том, что источником магнитного поля является электрический ток. Но каким образом можно вычислить вектор магнитной индукции поля, зная этот ток?

Для магнитного поля, также как и для электрического, справедлив принцип суперпозиции электрических полей. Справедливость этого принципа нельзя доказать теоретически. Он подтверждается только экспериментально.

Суть этого принципа состоит в следующих двух положениях.

1) Если ток I₁создаёт в некоторой точке пространства магнитное поле, то этот вектор магнитной индукции не изменится при появлении других токов:I₂,I₃, …,I_n. Это означает, что появление новых токов и новых полей не искажает индукциимагнитного поля исходного токаI₁.

2) Если магнитное поле создаётся несколькими токами, то индукция такого поля равна векторной сумме магнитных индукций складываемых полей:

(8.4)

Эти положения многократно подтверждены экспериментально.

Теперь применим принцип суперпозиции для расчёта магнитного поля электрического тока: вектор магнитной индукции поля, созданного электрическим током, равен векторной сумме магнитных индукций от отдельных элементов этого тока:

.

Для окончательного решения этой задачи нужно только знать, какое поле создаёт элемент тока.

В решении этой проблемы добились успеха французские учёные: физики экспериментаторы Био и Савар и математик Лаплас. Они установили, что вектор магнитной индукции поля, созданного элементом тока , равен:

(закон Био-Савара-Лапласа, 1820 г.), (8.5)

здесь: — элемент тока;

— радиус-вектор, проведённый от элемента тока в точку, где вычисляется магнитное поле (рис. 8.5.)

Рис. 8.5.

Таким образом, был найден «элементарный кирпичик» магнитного поля. Зная поле элемента тока (8.5), можно теперь, опираясь на принцип суперпозиции магнитных полей, рассчитать поле любого тока.

Прежде, чем перейти к примерам расчёта магнитных полей, напомним, что точно тот же самый метод мы использовали и при рассмотрении электростатических полей. Что являлось «элементарным кирпичиком» электростатического поля? Поле точечного заряда. А далее, используя принцип суперпозиции электрических полей, мы получали возможность рассчитать поле любого заряда, разделяя его на составляющие точечные заряды.