2. Пример расчёта силы тока в проводящей среде

Пространство между обкладками сферического конденсатора заполнено проводящей средой с удельной электропроводимостью . Какой ток потечёт в таком конденсаторе, если потенциалы электродов₁и₂поддерживать постоянными (рис. 6.6.)?

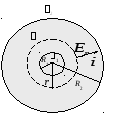
Рис. 6.6.

Задача обладает сферической симметрией. Выделим сферическую эквипотенциальную поверхность радиуса r. Во всех точках этой поверхности не только потенциал одинаков, но и плотность тока по величине одна и та же (6.13):

i=E_r,

где E_r— напряжённость поля в проводящей среде на поверхности выделенной сферыr. Это поле совпадает с электростатическим полем в вакууме при разности потенциалов на обкладках конденсатораU=₁–₂. Несложно показать, что для сферического конденсатора:

.

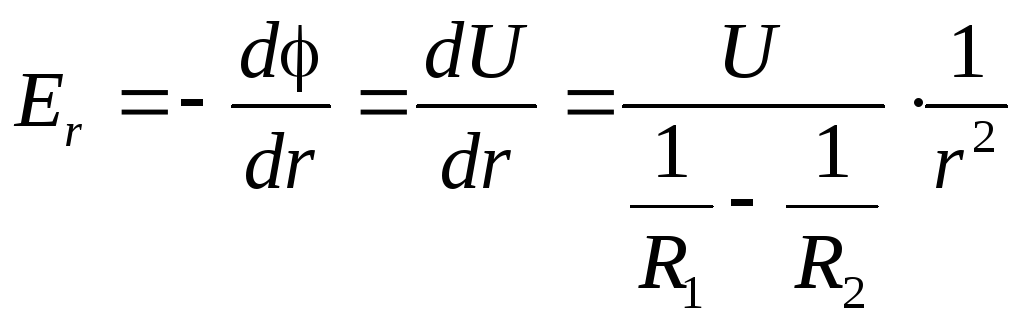(При выводе этого выражения, можно воспользоваться следующими ранее полученными соотношениями: (2.19),(4.8),(4.5)).

Теперь, воспользовавшись законом Ома в дифференциальной форме, вычислим плотность тока

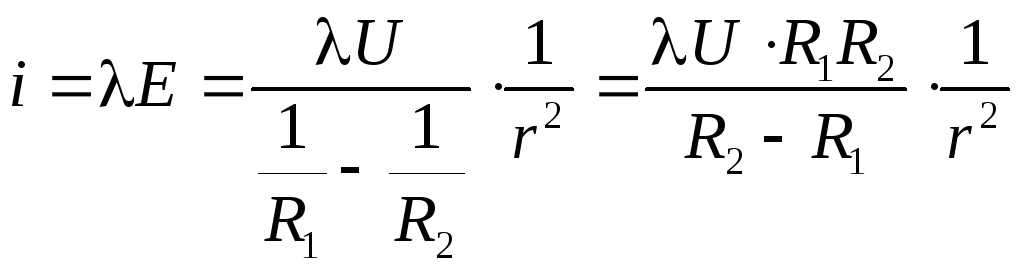
и полный ток, протекающий через замкнутую поверхность выделенной сферы:

.

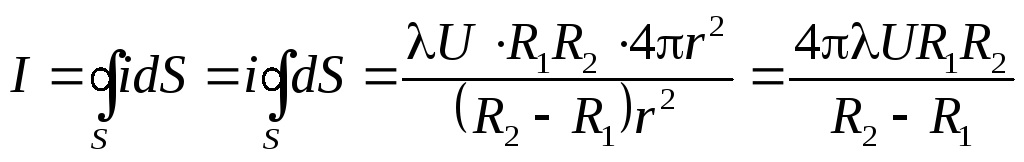Величина этого тока не зависит, конечно, от радиуса rвыделенной сферической поверхности:If(r). Зная закон сохранения электрического заряда, этот результат можно было бы предсказатьa priori.

Теперь легко вычислить электрическое сопротивление проводящего слоя в конденсаторе:

.

Нелишне ещё раз напомнить, что здесь — удельное сопротивление среды,R—сопротивление проводящего слоя, а вотR₁иR₂—радиусысферических обкладок конденсатора.

3. Закон Джоуля-Ленца в интегральной и дифференциальной формах

Пусть на участке электрической цепи протекает постоянный ток I(рис. 6.7.). НапряжениеUна концах этого участка численно равно работе, совершаемой электрическими силами при перемещении единичного положительного заряда по этому участку. Это следует из определения напряжения (см. 3.16).

.

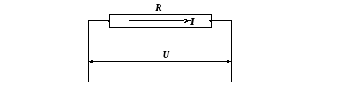
Рис. 6.7.

Отсюда работа A=qU. За времяtпо участку будет перенесён зарядq=Itи при этом будет совершена работа:

A=qU=UIt. (6.14)

Это выражение работы электрического тока справедливо для любых проводников.

Работа, совершаемая в единицу времени — мощность электрического тока:

. (6.15)

В системе СИ мощность измеряется в ваттах:

1 Вт = 1 Дж/1 с = 1 В 1 А.

Работа электрического тока (6.14) может затрачиваться на нагревание проводника, совершение механической работы (электродвигатель) и на химическое действие тока при его течении через электролит (электролиз).

Если химическое действие и механическая работа при течении тока не производятся, то вся работа электрического тока расходуется только на нагревание проводника:

Q=A=UIt=I²Rt. (6.15)

Закон о тепловом эффекте электрического тока (6.15) был экспериментально установлен независимо английским учёным Д. Джоулем и русским академиком Э.Х. Ленцем. Формула (6.15) — математическая запись закона Джоуля-Ленца в интегральной форме, позволяющая вычислить количество теплоты, выделяющейся в проводнике. Для того, чтобы характеризовать тепловой эффект тока в различных точках проводника, выделим в нём элементарный участок трубки тока (рис. 6.8.). Запишем для этого элемента закон Джоуля-Ленца:

.

Здесь мы использовали хорошо известные соотношения:

— сопротивление участка;

i=E— закон Ома в дифференциальной форме;

dV=dldS— объём выделенного элемента трубки тока.

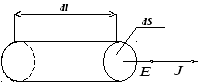
Рис. 6.8.

Разделив количество выделившейся теплоты dQна времяdt, получимтепловую мощность электрического тока:

,.

Отнеся эту величину к объёму элемента трубки тока, придём к удельной тепловой мощности:

. (6.16)

Перед нами закон Джоуля-Ленца в дифференциальной форме.

Учитывая, что i=E= , это выражение можно записать ещё и так:

,.

Подводя итог, ещё раз запишем формулы законов постоянного тока, рассмотренные на этой лекции.

Закон Ома для участка цепи:

в интегральной форме: ;

в дифференциальной форме: .

Закон Джоуля-Ленца:

в интегральной форме: Q=I²Rt;

в дифференциальной форме: Р_уд=Е²=.