Лекция 5 «Электрическое поле в диэлектриках»
План лекции
1. Типы диэлектриков. Поляризация диэлектриков. Поляризуемость и вектор поляризации.
2. Диэлектрическая проницаемость. Вектор электрического смещения.
3. Законы электрического поля в диэлектриках.
3.1. Закон Кулона.
3.2. Теорема Остроградского-Гаусса.
4. Граничные условия для электрического поля на поверхности раздела двух диэлектриков.
На прошлой лекции рассматривалось явление электростатической индукции — разделение зарядов проводника в электрическом поле. Свободные заряды в проводнике перемещаются под действием внешнего поля до тех пор, пока результирующее электрическое поле внутри проводника не окажется равным нулю. В связи с этим говорят, что проводник «разрушает электрическое поле, низводя его напряжённость до нуля».
Из школьного курса известно, что и
диэлектрики оказывают заметное влияние
на электрическое поле: напряжённость
поля в диэлектрике уменьшается в раз по сравнению с полем в вакуумеЕ0:
.
Здесь— диэлектрическая
проницаемость вещества.
Такое влияние диэлектрика на электрическое поле обусловлено поляризацией диэлектрика.
Явление поляризации и законы электрического поля в диэлектриках — тема настоящей лекции.
Типы диэлектриков. Поляризация диэлектриков. Поляризуемость и вектор поляризации.
Главное отличие диэлектриков от проводников состоит в том, что в диэлектриках отсутствуют свободные носители заряда. Заряженные частицы входят в состав атомов и молекул диэлектриков, но они не могут свободно перемещаться в межмолекулярном пространстве, что доступно, например, свободным электронам в металлических проводниках. Смещение зарядов в молекулах диэлектрика ограничено атомными масштабами.
Различают три типа диэлектриков: неполярные, полярные и ионные.
К неполярным диэлектрикам (N2,H2,O2,CO2и пр.) относятся
вещества, молекулы которых имеют
симметричное строение. В отсутствие
внешнего электрического поля центры
положительного и отрицательного зарядов
таких молекул совпадают. Другими словами,
их дипольный момент
равен нулю.
Молекулы диэлектриков второй группы — полярных — имеют асимметричное строение (H2O,CO,SO2и пр.). Такие молекулы и в отсутствие внешнего электрического поля имеют изначальный дипольный момент, отличный от нуля. Полярные молекулы принято условно изображать в виде гантельки (рис. 5.1.).
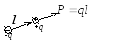
Рис. 5.1.
Кристаллическую структуру ионных диэлектриков (NaCl,KCl,KBrи др.) можно рассматривать как систему двух ионных решёток, вдвинутых одна в другую.
Теперь посмотрим, что будет происходить с молекулами диэлектриков в электрическом поле.
а) Неполярные диэлектрики
В диэлектрическом поле на положительные
и отрицательные заряды молекул будут
действовать равные и противоположные
силы, растягивающие молекулу (рис. 5.2.).
Действие этих сил приводит к деформации
молекул и к возникновению у них дипольного
момента:
.
Величина этого момента, как показывает
опыт, пропорциональна напряжённости
поля
,
поэтому такие молекулы называют ещё
упругими диполями.
Рис. 5.2.
б) Полярные диэлектрики
Полярные молекулы не меняют величину своего дипольного момента под действием электрического поля. В отличие от неполярных молекул, они ведут себя как жёсткие диполи.
В электрическом поле на такую жесткую молекулу действует вращающий момент, стремящийся ориентировать дипольные моменты молекул вдоль поля (рис. 5.3.).
Рис. 5.3.
в) Ионные диэлектрики
В электрическом поле положительные и отрицательные подрешётки ионной структуры смещаются друг относительно друга, и при этом возникает дипольный момент.
Все эти явления, происходящие в диэлектриках в присутствии электрического поля, называются поляризацией. В первом случае это была деформационнаяполяризация, во втором —ориентационная, в третьем —ионная.
Обратимся к количественной мере этих процессов. Для определённости рассмотрим подробнее ориентационную поляризацию полярного диэлектрика.
Молекулы такого вещества имеют дипольные моменты. Но в отсутствиеэлектрического поля в однородном диэлектрике нет какого-либо преимущественного направления, и тепловое движение хаотически перемешивает дипольные моменты молекул таким образом, что суммарный момент молекул единицы объёма вещества равен нулю.
В электрическом поле на молекулы действуют вращающие моменты, стремящиеся ориентировать диполи вдоль поля. На границах диэлектрика при этом возникают «связанные» заряды с поверхностной плотностью +’ и –’ (рис. 5.4.).
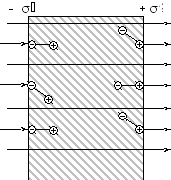
Рис. 5.4.
Степень поляризации диэлектрика в
электрическом поле характеризуется
вектором поляризации
,
равным векторной сумме дипольных
моментов всех молекул единицы объёма
вещества (теперь эта сумма не равна
нулю):
. (5.1)
Опыт показывает, что вектор поляризации
диэлектрика пропорционален напряжённости
поля
:
. (5.2)
Здесь: — диэлектрическая восприимчивость вещества;
0— знакомая нам электрическая постоянная.
В случае неполярного диэлектрика дипольный момент отдельной молекулы, как уже упоминалось, пропорционален напряжённости электрического поля:
. (5.3)
Здесь — поляризуемость молекулы.
Тогда суммарный дипольный момент всех молекул в объёме Vбудет равен:
.
Вектор поляризации (поляризованность) в этом случае, как и в случае полярного диэлектрика, оказывается пропорциональным напряжённости поля:
. (5.4)
Здесь диэлектрическая восприимчивость равна произведению числа молекул в единице объёма (n) и коэффициента поляризуемости ():
=n. (5.5)
Покажем, что вектор
поляризации
определяется величиной связанного
заряда’.
Рассмотрим однородно поляризованный
диэлектрик, выполненный в виде наклонной
призмы с основанием Sи ребромL, параллельным
вектору поляризации
(рис. 5.5).
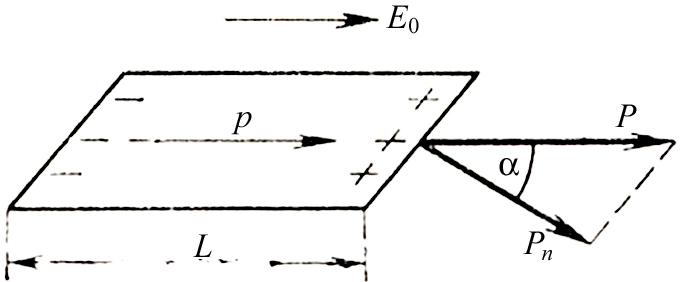
Рис. 5.5.
Электрический момент призмы равен q’L=’SL. Здесьq’ и’ — связанный заряд и плотность связанного заряда на основании призмы.
Учитывая, что объём призмы равен V=SLcos, этот же электрический момент представим в виде:
’ SL = P V = P SLcos = Pn SL.
Отсюда легко получить искомое соотношение:
’ =Pn. (5.6)
Этот результат позволяет сделать следующие заключения:
1. поверхностная плотность связанных зарядов равна нормальной составляющей вектора поляризации;
2. заряд, прошедший в процессе поляризации через единичную поверхность, нормальную к направлению смещения зарядов, равен модулю вектора поляризации.