Вопрос 43. Система линейных уравнений, однородная и неоднородная система, решение системы, совместная и несовместная система, эквивалентные системы

Системой  линейных алгебраических уравнений с  неизвестными называется система уравнений вида

Числа  называются коэффициентами системы;  — свободными членами,  — неизвестными. Количество  уравнений в системе может быть меньше, больше или равно числу неизвестных.

Система называется однородной, если все свободные члены равны нулю; в противном случае она называется неоднородной.

Решением системы называется упорядоченная совокупность  чисел  такая, что после замены неизвестных  соответственно числами  каждое уравнение системы превращается в верное числовое равенство.

Система называется совместной, если она имеет хотя бы одно решение. Если система не имеет ни одного решения, то она называется несовместной.

Две системы уравнений называются эквивалентными, если множество их решений совпадают

Вопрос 44. Матрица системы линейных уравнений, матричная форма записи системы

Исходную Системой линейных алгебраических уравнений можно записать в матричном виде:

 ,

где матрица  называется матрицей системы, это матрица, составленная из коэффициентов при неизвестных;  - вектором-столбцом неизвестных,  - вектором-столбцом правых частей или свободных коэффициентов.

Вопрос 45. Правило Крамера

Системой однородных линейных уравнений называется система вида

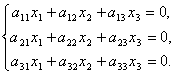
Ясно, что в этой случае , т.к. все элементы одного из столбцов в этих определителях равны нулю.

Так как неизвестные находятся по формулам , то в случае, когда Δ ≠ 0, система имеет единственное нулевое решение x = y = z = 0. Однако, во многих задачах интересен вопрос о том, имеет ли однородная система решения отличные от нулевого.

Вопрос 46. Минор к-ого порядка, ранг матрицы, базисный минор

Определитель, который образован элементами матрицы, стоящими на пересечении произвольно выбранных k строк и k столбцов, называется минором k-го порядкаэтой матрицы ( при этом минор 1-го порядка – это произвольный элемент данной матрицы).

Рангом матрицыназывается наивысший порядок ее миноров, отличных от нуля (ранг нулевой матрицы полагается равным нулю). Ранг матрицы А обозначается символомr(А).

Всякий неравный нулю минор, порядок которого равен рангу матрицы, называется ее базисным минором.

Вопрос 47. Элементарные преобразования над матрицами

Элементарными преобразованиями матрицы называются следующие 4 операции:

1. перестановка двух строк (столбцов)

2. умножение строки (столбца) на число, неравное нулю

3. прибавление к строке (столбцу) другой строки ( другого столбца), умноженной (умноженного) на любое число

4. отбрасывание нулевой строки (нулевого столбца)

Вопрос 48. Теорема об элементарных преобразованиях

Ранг матрицы не меняется при ее элементарных преобразованиях.

Вопрос 49. Теорема Кронекера-Капелли

Теорема Кронекера-Капелли. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы.

Система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

Решить систему — это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение.

 

Вопрос 50. Условия существования ненулевого решения у однородной системы mхn и системы nхn

Условия существования ненулевого решения у однородной системы mхn:однородная система mхn имеет ненулевое решение тогда и только тогда, когда ранг матрицы системы меньше числа неизвестных.

Условия существования ненулевого решения у однородной системы nхn:однородная система nхn имеет ненулевое решение тогда и только тогда, когда определитель системы равен нулю.

Вопрос 51. Изображение на числовой оси множеств действительных чисел, заданных равенством и неравенством

52. Модуль действительного числа и его свойства

Модулем неотрицательного действительного числа х называют само это число: | х | = х; модулем отрицательного действительного числа х называют противоположное число: I х | = - х.

INCLUDEPICTURE "http://school.xvatit.com/images/f/f3/14-06-125.jpg" \* MERGEFORMATINET

1. |а| 0.

2.|аb| =|a| |b|.

INCLUDEPICTURE "http://school.xvatit.com/images/b/b2/14-06-127.jpg" \* MERGEFORMATINET

53. Геометрический смысл модуля числа и модуля разности двух чисел

Геометрический смысл – расстояние от точки с координатой Х на числовой прямой до начала координат.

Модуль разности – расстояние между соответствующими точками на числовой прямой.

54. Определение функции, определение графика функции

Функция (отображение, оператор, преобразование) — математическое понятие, отражающее связь между элементами множеств. Можно сказать, что функция — это «закон», по которому каждому элементу одного множества (называемого областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

График функции — понятие в математике, которое даёт представление о геометрическом образе функции.

В этом случае, график функции — это геометрическое место точек плоскости, абсциссы (x) и ординаты (y) которых связаны указанной функцией: точка располагается (или находится) на графике функции тогда и только тогда, когда INCLUDEPICTURE "http://upload.wikimedia.org/math/7/c/1/7c1c9491ba7c6e8d6d2cfa82e39b22ca.png" \* MERGEFORMATINET