Вопрос 27. Формула расстояния от точки до прямой, формулы вычисления угла между прямыми

Расстояние от точки до прямой:

Угол между двумя прямыми:

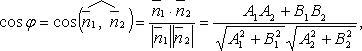
Вопрос 28. Условия параллельности и перпендикулярности двух прямых

Условия параллельности двух прямых:

а) Если прямые заданы уравнениями y = k₁x + B₁,y = k₂x + B₂, с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

k₁ = k₂.     

б) Для случая, когда прямые заданы уравнениями в общем виде A₁x + B₁y + C₁ = 0, A₂x + B₂y + C₂ = 0, необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями y = k₁x + B₁,y = k₂x + B₂,с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

Это условие может быть записано также в виде: k₁k₂ = -1. 

б) Если уравнения прямых заданы в общем виде A₁x + B₁y + C₁ = 0, A₂x + B₂y + C₂ = 0, то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства:

A₁A₂ + B₁B₂ = 0.  

Вопрос 29. Виды уравнений плоскости

1. уравнение плоскости, проходящей через данную точку с данным нормальным вектором:

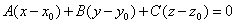
2. общее уравнение плоскости:

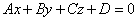
3. нормальное уравнение плоскости:

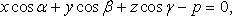
Вопрос 30. Формула расстояния от точки до плоскости, формулы вычисления угла между плоскостями

Расстояние от точки до плоскости:

Если две плоскости  и  заданы общими уравнениями вида:

 

Под углом между плоскостями ипонимается один из двугранных углов, образованных этими плоскостями.

Очевидно, что угол между иравен углу между их нормалями, то есть между векторами₁и₂.

Из формулыполучаем, чтокосинус угла между плоскостямии

равен

Вопрос 31. Условия параллельности и перпендикулярности двух плоскостей

Условие параллельности плоскостей заключается в параллельности нормалей , а условие перпендикулярности плоскостей – в перпендикулярности нормалей  или равенстве нулю их скалярного произведения: .

Вопрос 32. Виды уравнений прямой в пространстве

1. векторное:

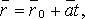
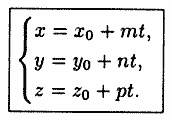
2) параметрическое:

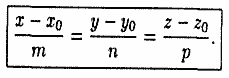
3) каноническое:

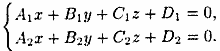
4) общее:

Вопрос 33. Кривые второго порядка: эллипс, гипербола, парабола (определения и их канонические уравнения)

Линиями второго порядка являются: эллипс (в частности окружность), гипербола, парабола, две прямые, одна прямая, одна точка и, наконец, линия не содержащая ни одной точки(т.е. просто пустое множество).

Общий вид уравнения второй степени с двумя переменными х и у:  

Ax² + 2Bxy + Cy² + 2Dx + 2Ey + F = 0 

1) Эллипсом называется множество всех точек плоскости, сумма расстояний каждой из которых до двух данных точек этой плоскости (называемых фокусами), есть величина постоянная (большая, чем расстояние между фокусами)

Каноническое уравнение эллипса: 

2) Гиперболойназывается множество всех точек плоскости, модуль разности расстояний каждой из которых до двух данных точек этой плоскости (называемых фокусами), есть величина постоянная ( положительная и меньшая, чем расстояние между фокусами).

Каноническое уравнение гиперболы:

3) Параболой называется множество всех точек плоскости, каждая из которых равноудалена от данной точки этой плоскости (называемой фокусом) и данной прямой, лежащей в этой плоскости и не проходящей через фокус ( она называется директрисой)

Каноническое уравнением параболы:  y² = 2px