Решение задач одномерной оптимизации методом золотого сечения

Пусть f(x) - функция, определенная на отрезке [a,b]. Функция f(x) называется унимодальной, если существует единственная точка х*, в которой f(x) принимает экстремальное значение. Так как max f = -min (-f), то в дальнейшем будем считать, что речь идет о минимуме функции f(x) отрезке [a,b].

Отметим, что унимодальная функция не должна быть гладкой, т.е. имеющей непрерывную производную, и даже непрерывной. Примеры унимодальных функций приведены на рисунке 1.

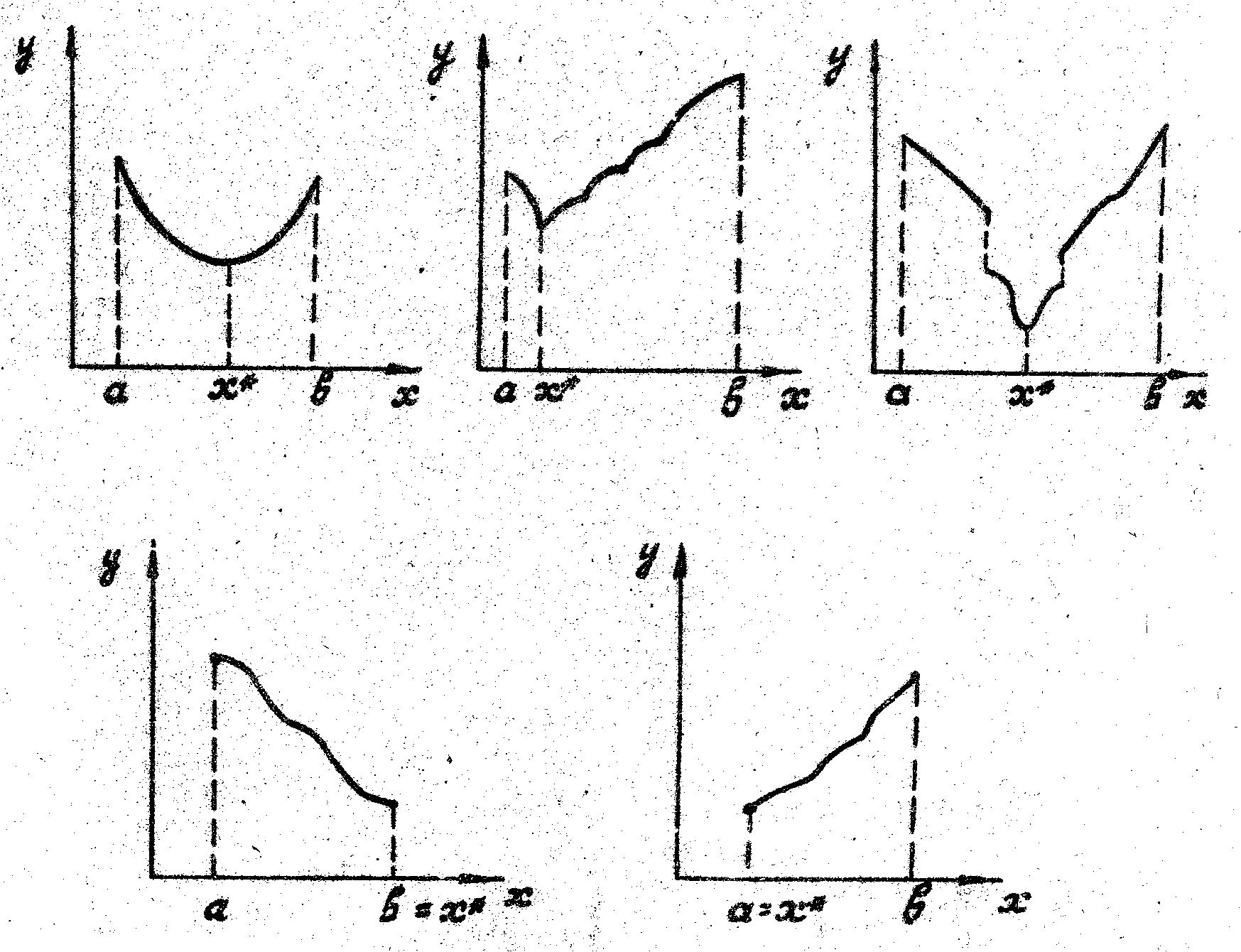
Рисунок 1-Унимодальные функции

Из определения унимодальности следует, что если Х₁<Х₂Х*, то f(Х₁)>f(Х₂). Аналогично, если Х*Х₁<Х₂, то f(Х₁)<f(Х₂).

Задача минимизации функция f(Х) состоит в построении такой последовательности чисел {Х_к}, для которой минимальное значение, функции f(X) будет находиться в интервале X_к-1X*X_к. Такой интервал называется интервалом неопределенности.

Алгоритм выбора абсцисс {Х_к} называется стратегией поиска. При заданном количестве вычислений функции наилучшей стратегией будет та, которая даст меньший интервал неопределенности. Известно, что оптимальной является стратегия Фибоначчи. Метод золотого сечения при достаточно большом количестве вычислений дает окончательный интервал неопределенности лишь на 17 % больше, чем метод Фибоначчи, однако организация вычислительного процесса в методе золотого сечения значительно проще.

Как известно, золотым сечением отрезка называют деление отрезка на две части так, что отношение длины всего отрезка к длине большей части равно отношению длины большей части к меньшей. Золотое сечение отрезка [a,b] производят две симметрично расположенные точки

Х₁=а + (1 - )*(b - a);X₂=a + *(b - a),

где  =(5-1)/2=0,6180339. Точка Х₁, в свою очередь, производит золотое сечение отрезка [а, X₂], а точка Х₂ - золотое сечение отрезка [X₁, b].

Алгоритм поиска минимального значения функции f(Х) на отрезке [a, b] заключается в следующем. Начальный отрезок [a, b] делим точками Х₁ и Х₂ по "правилу золотого сечения" и в точках Х₁ и Х₂ вычисляем значения функций f(X₁) и f(X₂). Если f(X₁)<f(X₂), то для дальнейшего деления берем отрезок [a, X₂]. Если же f(X₁)>f(x₂), то берем отрезок [X₁, b]. Покажем это.

Пусть f(X₁)<f(X₂), то для дальнейшего рассмотрения берем отрезок [a, X₂], т.е. считаем Х* расположенным левее точки Х₂. Действительно, предположим, что оптимум Х*>X₂, т.е. расположен наоборот правее точки Х₂, но тогда Х₁ и Х₂ будут находиться с одной стороны от оптимума: X₁<X₂<X*. По определению унимодальности это означало бы, что f(X₁)>f(X₂), но это противоречит условию f(X₁)<f(X₂). Аналогично, если f(X₁)>f(X₂).

В первом случае одной из двух точек, делящих в золотом отношении отрезок [a, X₂], будет точка Х₁, а во втором для отрезка [X₁, b] - точка Х₂. Это следует из свойств золотого сечения. Таким образом, из двух значений функции, необходимых на новом шаге расчета, вычисляется всего одно: другое было получено на предыдущем шаге вычислений. Итак, на каждом шаге поиска, начиная со второго, требуется лишь одно вычисление функции, и интервал неопределенности уменьшается в (0,618)^-1 раз. Итерации продолжаются до тех пор, пока интервал неопределенности не станет меньше некоторого заданного достаточно малого положительного числа .

Алгоритм поиска минимума функции f(X) на отрезке [a, b] поясняется на рисунке 2

Рисунок 2-Поиск минимума методом золотого сечения

Meтод золотого сечения аналогичен методу половинного деления, применяемого при нахождении корней алгебраических и трансцендентальных уравнений, в том смысле, что он гарантирует нахождение минимума в самых неблагоприятных условиях.