Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

ГОУ ВПО «Магнитогорский государственный технический университет

им. Г.И.Носова»

Кафедра химической технологии неметаллических материалов

и физической химии

РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ 1

По курсу «Физическая химия»

раздел «Термодинамика»

вариант 1-2

Выполнил: Студент гр. МСЭ-10 Айменов Н.К.

Проверил: Доц., канд. техн. наук Смирнов A.H.

1.Формулировка задания

Исследование 1

Дана реакции 2AlCl₃+3H₂=2Al+6HCl . Выполнить следующее:

1. Составить уравнение зависимости от температуры величины теплового эффекта ∆H⁰т = f(T) и изменения энтропии ∆S⁰т = f(T).

2. Вычислить величины ∆Ср, ∆Н⁰т, ∆S⁰т, ∆Gт и lnKр при нескольких температурах, значения которых задаются температурным интервалом (300 – 440) и шагом температур = 20. Полученные значения используются при построении графиков в координатах ∆Ср – Т; ∆Н⁰т – Т; ∆S⁰т - Т; ∆G⁰т – Т и lnKр – 1/Т.

3. Пользуясь графиком lnKр – 1/Т , вывести приближенное уравнение вида lnKр = А/Т + В, где А,В – постоянные.

Исследование 2

1. Используя правило фаз Гиббса для рассматриваемой системы, определить количество фаз независимых компонентов и число степеней свободы.

2. Определить возможное направление протекания исследуемой реакции и равновесный состав газовой фазы при давлении Робщ = 101,3 кПа, и температуре Т = 500К. При решении задачи использовать выведенное в исследовании 1 эмпирическое уравнение lnKр = А/Т + В и данные об исходном составе газовой фазы ( Н₂ = 50%, НСl = 50%).

3. Установить направление смещения состояния равновесия рассматриваемой системы при:

а) увеличении давления (постоянная температура );

б) увеличении температуры (постоянное давление).

3.1. Исследование 1

Таблица 2

Исходные данные для термодинамического исследования реакции

2AlCl₃+3H₂=2Al+6HCl

№ п\п	Вещество	∆H⁰₂₉₈, КДж/моль	S⁰₂₉₈, Дж/моль∙К	Коэффициенты a+bt+c’T⁻²,	в Дж/моль∙К	уравнение
				a	b*10³	c’∙10⁻⁵
1	AlCl₃	-697400	167,00	55,44	117,15	0
2	H₂	0	130,60	27,28	3,26	0,50
3	Al	0	25.31	20,67	2,39	0
4	HCl	-96420	186,80	28,05	3,52	-

3.1.1. Расчет изменения изобарной теплоемкости ∆Сp и теплового эффекта реакции ∆н⁰т

Зависимость теплового эффекта реакции от температуры определяется законом Кирхгофа

∆Н⁰т = ∆Н⁰₂₉₈ + ∆CpdT , (1)

где ∆Н⁰₂₉₈ - стандартный тепловой эффект реакции при 298 К;

∆Cp - изменение теплоемкости системы в результате протекания реакции.

Последняя величина рассчитывается по уравнению

∆Cp = Σ(niCp,i) кон –Σ(niCp,i) исх , (2)

Где Cp,i- мольная изобарная теплоемкость i-го вещества определяемая из уравнения

Сp,i = ai + biT + ci’T⁻² (3)

ni - стехиометрический коэффициент i-го вещества в уравнении реакции.

Для исследуемой реакции, после подстановки в уравнение (2) ni , оно примет вид

∆Cp=(6 Cp + 2Cp )-(2 Cp + 3 Cp ) (4)

Определим температурные зависимости Сp,i для всех реагентов, используя уравнение (2) и термодинамические данные в табл. 2:

Cp =55,44+117,15∙10⁻³T; (5a)

Cp =27,28+3,26∙10⁻³Т+0,5∙10⁵Т⁻² (5b)

Cp =20,67+2,39∙10⁻³Т (5с)

Cp =28,05+3,52∙10⁻³Т (5d)

Определим расчетные уравнения ∆Cp = f(T) для исследуемой реакции. Для чего подставим уравнения (5а, 5b, 5c и 5d) в уравнение (4). После подстановки получим

∆Cp=[6(28,05+3,52∙10⁻³Т)+2(20,67+2,39∙10⁻³Т)]-[2(55,44+117,15∙10⁻³Т)+3(27,28+3,26∙10⁻³Т+0,5∙10⁵Т⁻²)] = 16,92-218,18∙10⁻³-1,5∙10⁵T⁻².

Рассчитаем значение ∆Cp при различных температурах и сведем эти значения в табл. 3. При шаге по температуре в 20 К необходимо рассчитать ∆Cp при следующих температурах: 300, 320, 340, 360, 380, 400, 420 и 440 К.

Таблица 3

Величина ∆Cp при различных температурах для реакции

2AlCl₃ + 3H₂ = 2Al + 6HCl

Т, К	298	300	320	340	360	380	400	420	440
∆Cp, Дж/К	-4,47	-4,5	-4,8	-5,1	-5,4	-5,7	-6	-6,3	-6,6

По данным табл. 3. Строим зависимость ∆Cp=f(T) , как на рис.1.

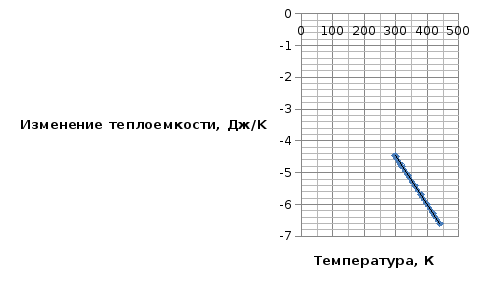
Рис. 1. Зависимость изменения изобарной теплоемкости от температуры

Значение ∆Н⁰₂₉₈ в уравнении (1) определяется по стандартным теплотам образования ∆Н⁰₂₉₈‚i

∆Н⁰₂₉₈ = Σ(niH⁰₂₉₈ i )кон – Σ(niH⁰₂₉₈,i )исх (7)

В рассматриваемом случае уравнение (7) имеет вид

∆Н⁰₂₉₈ = (6∆Н ₂₉₈ + 2∆Н ₂₉₈) – (2∆Н ₂₉₈ + 3∆Н⁰₂₉₈) (8)

или в числовом виде

∆Н⁰₂₉₈ = (-96,46∙6-2∙0)-(-697,4∙2) = -578,76+1394,8 = 816040 Дж.

Чтобы в дальнейшем избежать ошибки при расчете∆Н⁰т, необходимо теплоты образования реагентов в табл. 2 из килоджоулей перевести в джоули.

В соответствии с заданием необходимо рассчитать тепловые эффекты в интервале температур 300-440 К. То есть для исследуемой реакции, в интервале температур 300-440 К, после подстановки численных значений ∆Н⁰₂₉₈ и уравнения (6) в уравнение (1), получим уравнение зависимости теплового эффекта для первой реакции от температуры:

∆Н⁰ = ∆Н⁰₂₉₈ + 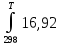dT - 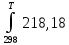∙10⁻³TdT-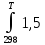∙10⁵T⁻²dT =

816040+16,92(Т-298)-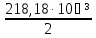(Т²-298²)+1,5∙10⁵(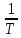-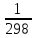). (9)

После подстановки значений температур в уравнение (9) получим тепловые эффекты, значения которых сведем в табл. 4.

Таблица 4

Величина ∆Н⁰ при различных температурах для реакции

2AlCl₃₍тв₎ + 3H₂₍г₎ = 2Al₍тв₎+6HCl₍г₎

Т, К	298	300	320	340	360	380	400	420	440
∆Н⁰Т, кДж	816,04	815,94	814,89	813,76	812,55	811,25	809,87	808,40	806,84

Зависимость ∆Н⁰Т = f(T), построенная по данным табл. 3, представлена на рис. 2.

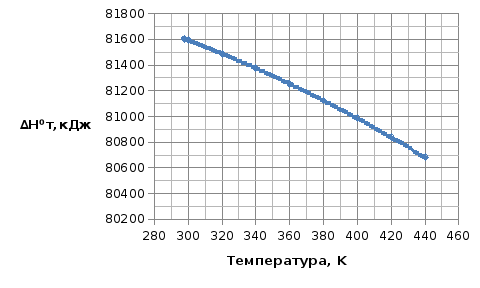
Рис. 2. Зависимость теплового эффекта реакции 2AlCl₃+3H₂=2Al+6HCl от температуры

tgα = ∆C⁰i,₃₆₀ = = = 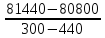- 4,5Дж/К.