Глава 3. Уравнения движения электропривода

Наиболее удобным методом составления уравнения движения механической части привода являются уравнения движения Лагранжа второго рода. При этом предполагается, что движение механической части исследуется в системе обобщенных координат, в качестве которых должны быть приняты независимые параметры, определяющие положения механизма. Такими параметрами являются углы поворота вращающихся вокруг неподвижных осей дискретных инерционных элементов и их линейные перемещения (рис. 3.1).

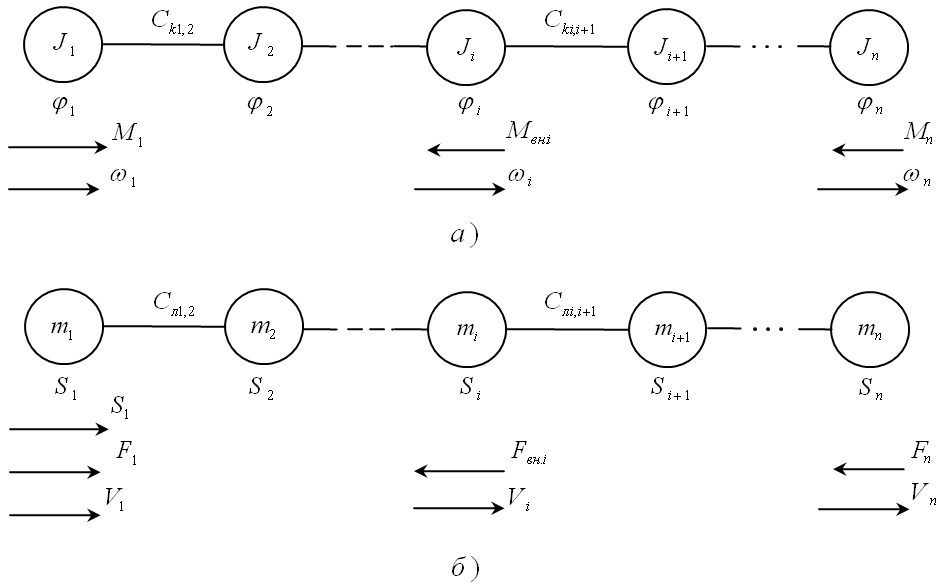
Рис. 3.1 Расчетные схемы механической части (а – для вращающихся элементов, б – для поступательно-движущихся элементов)

Уравнения Лагранжа второго рода

, (3.1)

где – кинетическая энергия систем;

–потенциальная энергия системы;

–работа сил рассеяния (диссипативная функция Релея);

–обобщенная координата;

–обобщенная скорость;

–обобщенная внешняя сила, соответствующая обобщенной координате.

При вращательном движении , ; при поступательном движении , , .

Число уравнений Лагранжа второго рода для системы равно числу дискретных инерционных элементов, т.е. числу степеней свободы механизма.

Для механической системы, содержащей инерционных и упругих элементов:

или ; (3.2)

или ; (3.3)

или . (3.4)

Моменты (силы), входящие в левую часть уравнения Лагранжа (1) и действующие на 1-й инерционный элемент системы, определяются как:

1) инерционные

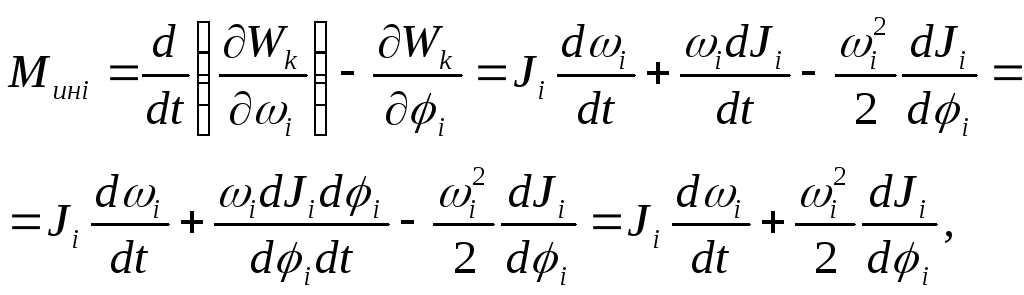(3.5)

где ;

2) потенциальные

; (3.6)

. (3.7)

3) диссипативные

; (3.8)

. (3.9)

Для (для первой массы)

. (3.10)

Производная (момент)

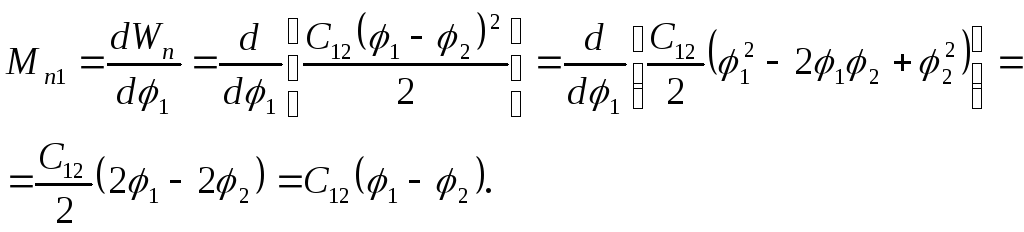(3.11)

Для

. (3.12)

Производная (момент)

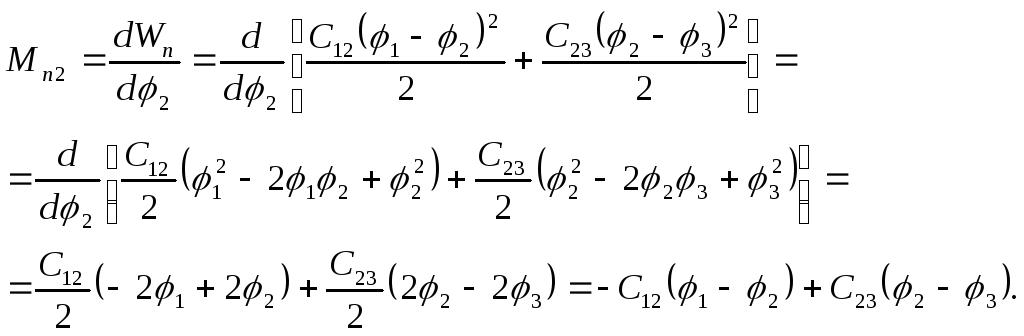(3.13)

В соответствии с уравнением Лагранжа (1) для любого i-го звена может быть записано уравнение движения

; (3.14)

, (3.15)

где ,– суммарный внешний момент (сила), действующий наi-е звено.

В тех случаях, когда момент инерции (масса) звена не зависит от его положения, , получим

; (3.16)

, (3.17)

где – угловое и линейное ускорение.

Диссипативные силы в упругих связях, обусловленные силами вязкого трения существенно меньше потенциальных сил, в связи с чем при исследовании законов движения электроприводов механизмов в первом приближении их можно не учитывать.

С учетом указанных допущений уравнения движения в случае трехмассовой системы имеют следующий вид

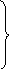
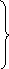(3.18)

Для двухмассовой системы

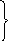
(3.19)

С учетом, что момент упругой связи уравнения (3.19) запишутся в следующем виде

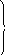
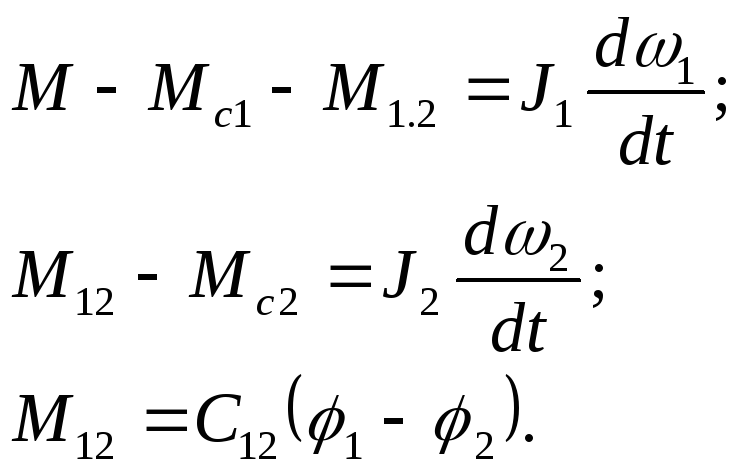(3.20)

Для одномассовой абсолютно жесткой системы на основании (3.5) при можно записать уравнение движения

, (3.21)

а при

. (3.22)

Глава 4. Механическая часть электропривода как объект управления

Двухмассовая упругая система (рис. 2.2, б) является основным объектом при инженерных исследованиях динамических процессов с учетом упругих связей, в которой коэффициентом пропорциональности учитывается момент внутреннего вязкого трения (диссипативные силы)

. (4.1)

Структурная схема двухмассовой упругой Э.М.С. представлена на рис. 4.1, которая составлена на основании системы дифференциальных уравнений в операторном виде, где

(4.2)

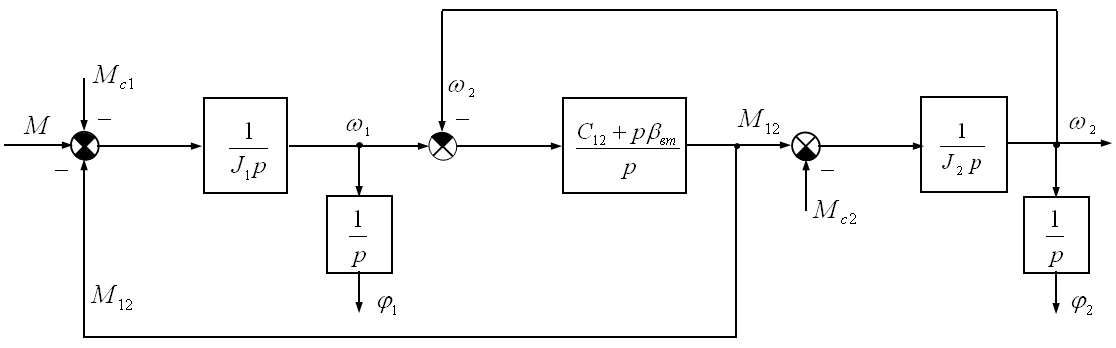
Рис. 4.1. Структурная схема двухмассовой упругой Э. М. С.

В рассматриваемой структурной схеме управляющем воздействием является электромагнитный момент двигателя М, а возмущающими воздействиями – моменты сопротивлений . В качестве выходных координат можно рассматривать скорости, упругий моменти углы перемещения инерционных масс

. (4.3)

Структурная схема двухмассовой системы электропривода (рис.4.1) позволяет получить передаточные функции по управляющему и возмущающим воздействиям для анализа поведения выходных координат ,.

По управляющему воздействию при после структурных преобразований в схеме (рис.4.1) передаточная функция по выходной переменнойопределяется следующим образом (см. рис. 4.2)

Рис. 4.2. Преобразованная структурная схема по двухмассовой системы при

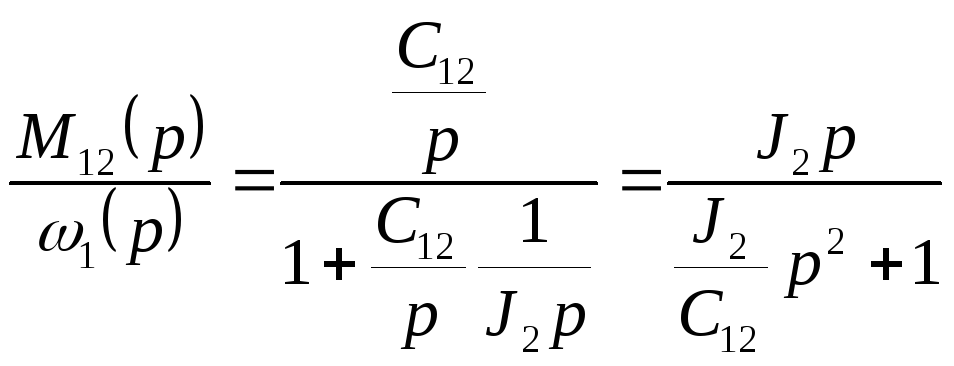; (4.4)

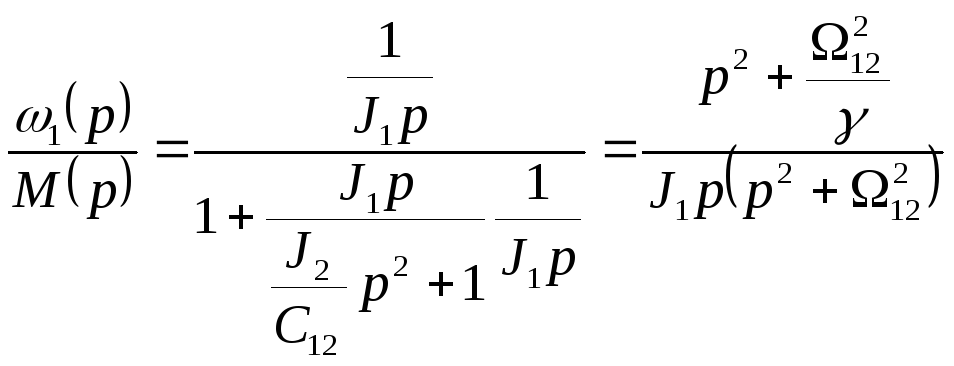, (4.5)

где 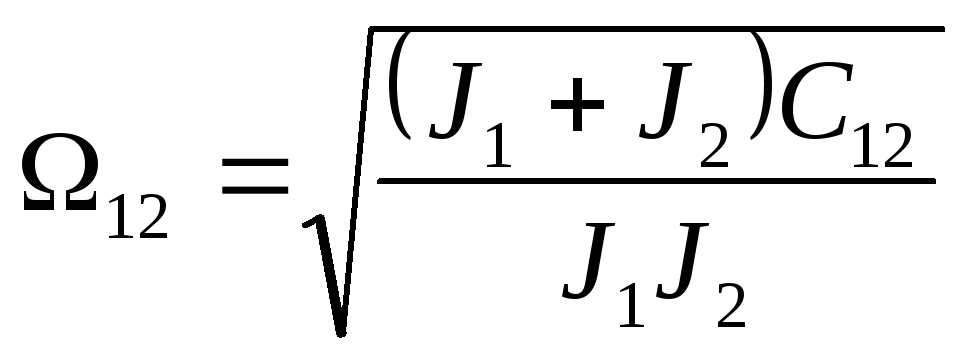– частота свободных колебаний двухмассовой упругой системы;

.

Передаточная функция по выходной переменной после структурных преобразований схемы (рис. 4.3) приопределяется следующим образом

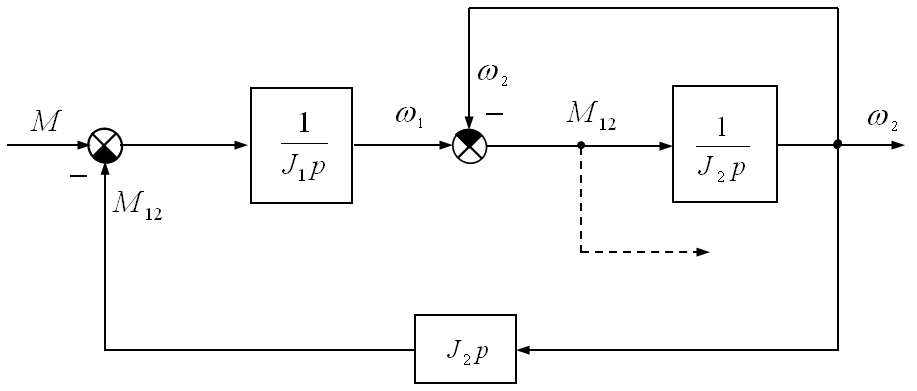
Рис. 4.3. Преобразованная структурная схема по двухмассовой системы при

.

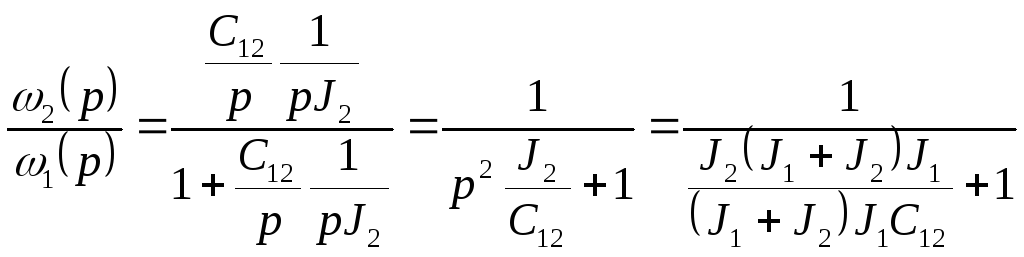С учетом

;

,

получим

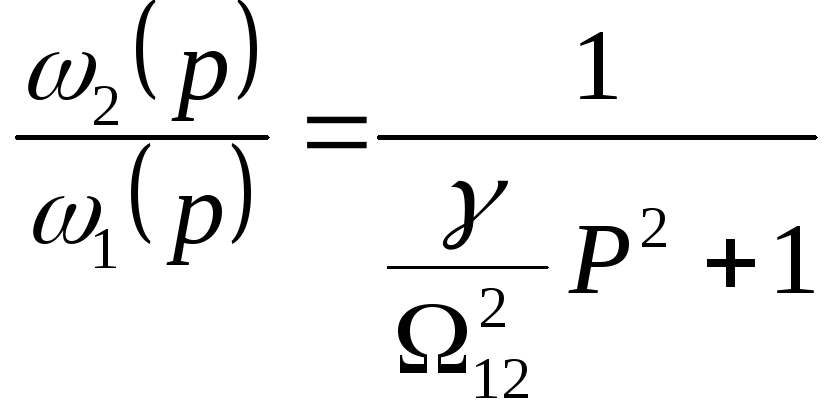. (4.6)

Уравнение (4.5) представим в следующем виде

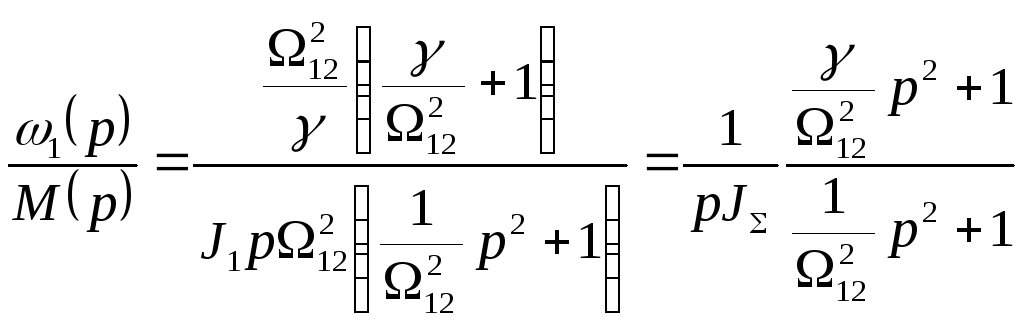. (4.7)

Тогда имеем структурную схему по выходной координате (см. рис. 4.4)

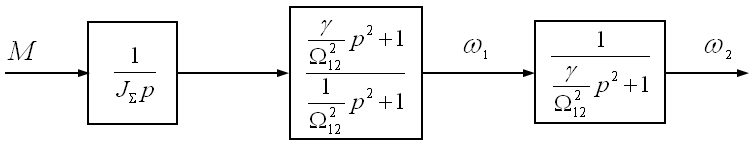
Рис. 4.4 Структурная схема по выходной координате

Передаточная функция

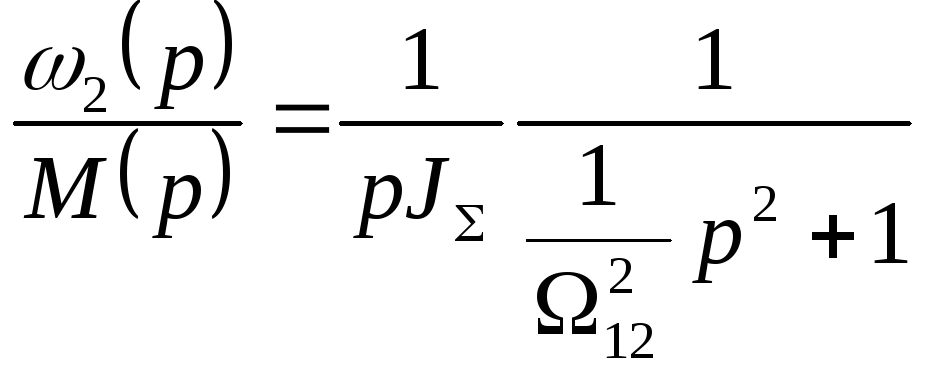, (4.8)

т.е. соответствует двум последовательно соединенным звеньям интегрирующего и колебательного.

Передаточная функция по выходной координате в соответствии со структурными преобразованиями в схеме рис. 4.1. приможет быть определена следующим образом.

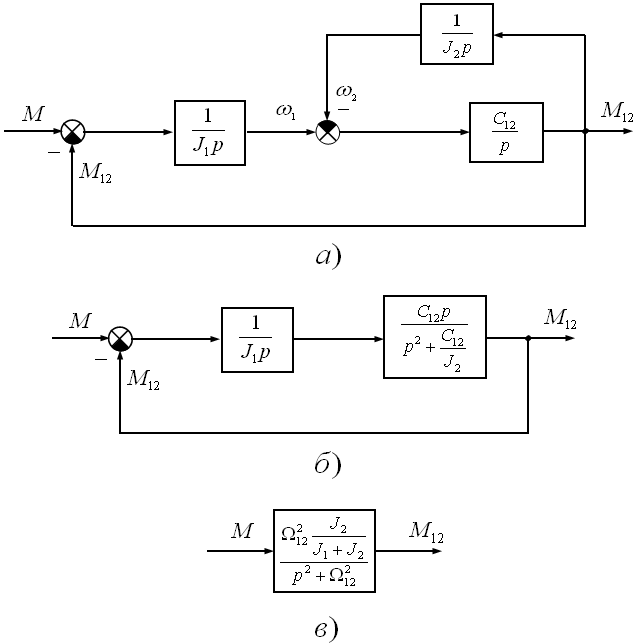
Рис. 4.5. Структурные преобразования для получения передаточной функции

Для схемы рис. 4.5, а передаточная функция

, (4.9)

а для схемы рис.4.5, б передаточная функция

. (4.10)

После соответствующих преобразований в формуле 4.10 получим

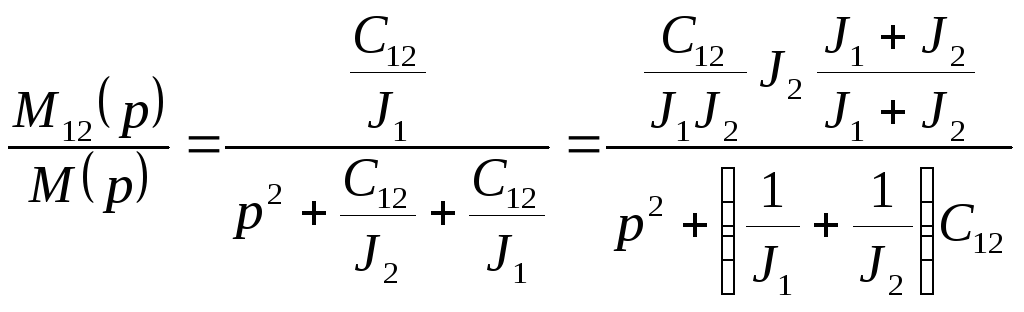
и окончательно

. (4.11)

Как видно из полученных передаточных функций ,,характеристическое уравнение системы (знаменатель в формулах 4.5, 4.6, 4.11), описывающее движение двухмассовой системы при

, (4.12)

а корни

. (4.13)

Поведение такой системы рассмотрим на примере приложения управляющего воздействия в виде электромагнитного момента М, изменяющегося во времени по гармоническому сигналу с переменной частотой . Амплитудно-частотные и фазочастотные характеристики такой системы, полученных при помощи (4.8), имеют вид

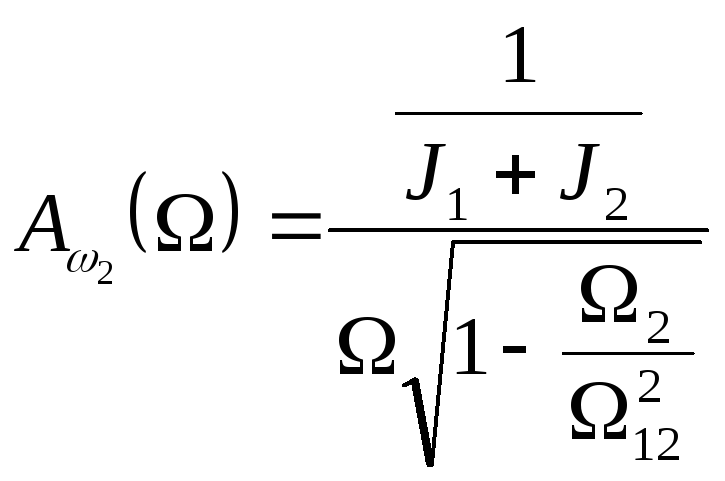; (4.14)

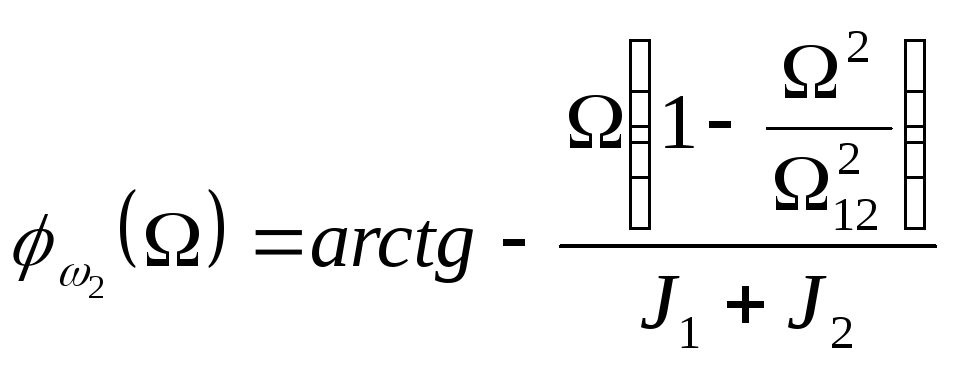. (4.15)

Анализ формул 4.14, 4.15 показывает, что при иамплитуды стремятся к бесконечности, а фазаприскачком изменяется на(). Зависимость,представлены на рис. 4.6, из которого следует, что принаступает механический резонанс,претерпевает разрыв, амплитуда колебаний возрастает до бесконечности.

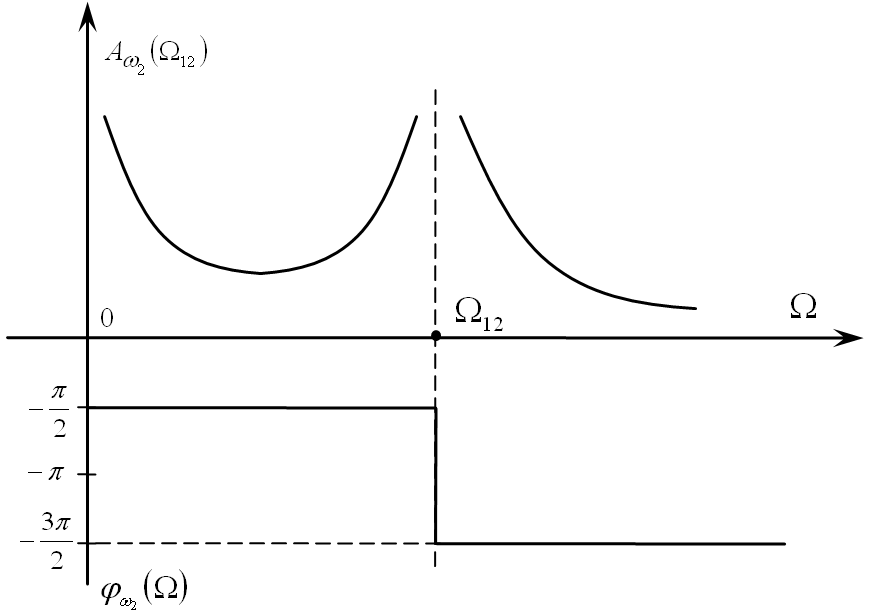
Рис. 4.6 Амплитудно-частотная АЧX и фазовая частотная ФЧХ характеристики двухмассовой системы

В реальных механических системах происходит ограничение резонансных амплитуд колебаний силами, обуславливающими рассеяние энергии механических колебаний. К внешним силам относятся трение колеблющейся системы о среду, к внутренним – диссипативные силы в упругих элементах (силы вязкого трения).

Система уравнений, описывающая движение двухмассовой системы с учетом сил вязкого трения (коэффициент β_в.т= β₁₂ ) представлена в виде (4.2), структурная схема на рис. 4.1.

Произведя структурные преобразования схемы рис. 1.2, получим передаточную функцию по управляющему воздействию

. (4.16)

Если обозначить

;

,

то уравнение (4.16) запишется в виде

. (4.17)

Корни характеристического равнения системы

. (4.18)

Выражение (4.18) показывает, что силы вязкого терния вносят в систему затухание и двухмассовая упругая система приобретает свойства колебательного звена с коэффициентом затухания и частотой колебаний. Так как,.

Логарифмический декремент затухания , представляющий собой отношения двух последующих амплитуд колебаний(рис. 4.27), характеризует рассеяние энергии в упругом звене. Он может быть определен по известной величине действительной и мнимой части корней характеристического уравнения (4.18).

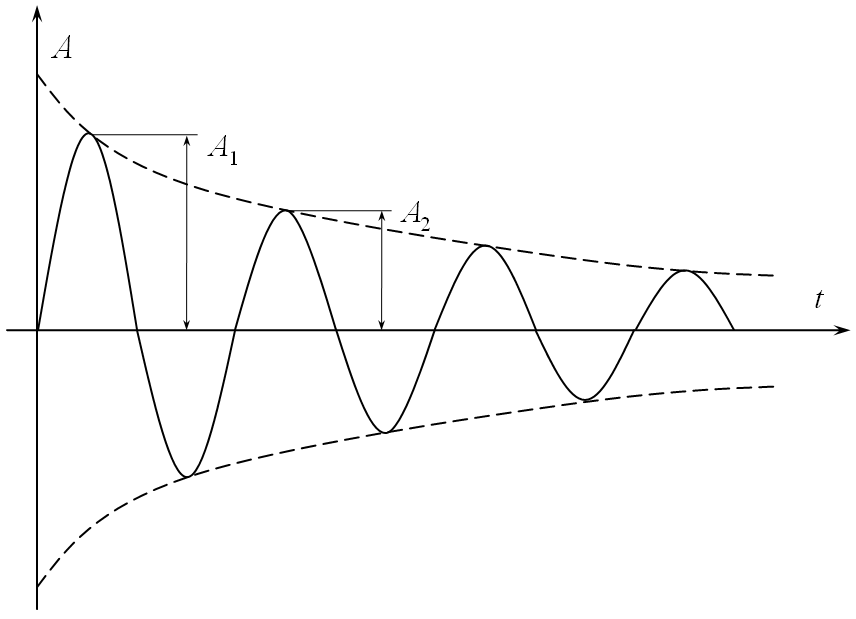
Рис. 4.7. К определению логарифмического декремента затухания

. (4.19)

Исследование показывают, что естественное механическое демпфирование обеспечивает значение . При таких значениях, несмотря на ограничение амплитуд резонансных колебаний, резонансный пик остается по-прежнему большим и колебания в зоне резонанса увеличиваются в (10-30) раз.

Выражение АЧХ для двухмассовой системы с учетом демпфирования принимает вид

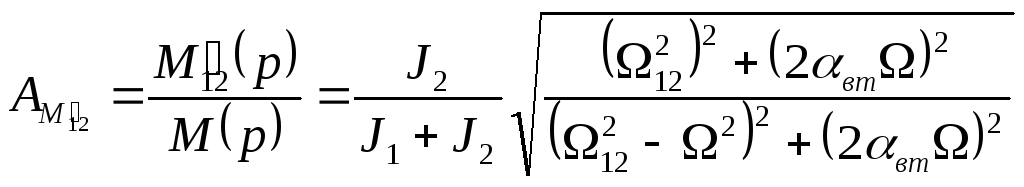. (4.20)

На рис. 4.8 приводятся зависимости резонансного коэффициента усиления системы от частоты, рассчитанные в соответствии с (4.20) для различных значений .

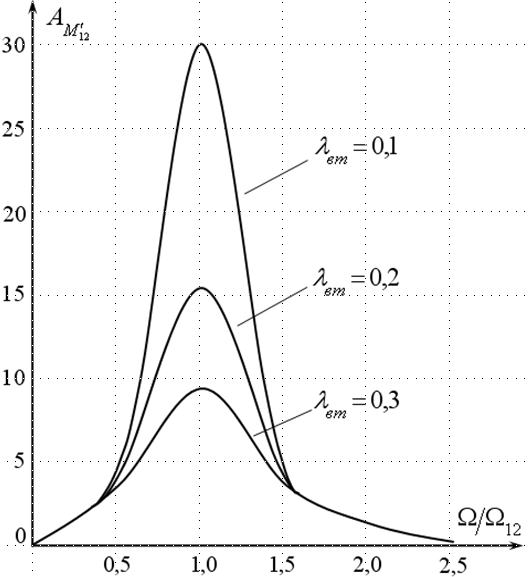
Рис. 4.8. Зависимости резонансного коэффициента усиления системы от частоты