
- •II.Элементы функционального и комплексного анализа.
- •Решение задачи:
- •6. Формула включений и исключений.
- •Упражнения и задачи по теории множеств
- •III. Введение в математический анализ. Дифференциальное исчисление функции.
- •Тема 1. Введение в математический анализ. Область определения функции совпадает с одз (областью допустимых значений) правой части, т.Е. С множеством всех значений х, при которыхвычисляется.
- •Вопросы для самопроверки:
- •Тема 2. Пределы
- •Вопросы для самопроверки:
- •Тема 3. Дифференциальное исчисление
- •Вопросы для самопроверки:
- •Тема 4. Приложения дифференциального исчисления
- •Вопросы для самопроверки:
- •Тема 5. Функции нескольких переменных
- •Вопросы для самопроверки:
- •Задачи для самоконтроля
- •IV. Интегральное исчисление функции одной переменной.
- •Тема 1. Неопределенный интеграл
- •Вопросы для самопроверки.
- •Тема 6. Определенный интеграл
- •Вопросы для самопроверки:
- •Задачи для самоконтроля
- •V. Дифференциальные уравнения.
- •Вопросы для самопроверки:
- •Задачи для самоконтроля
- •VI. Числовые и функциональные ряды. Числовые ряды
- •Функциональные ряды
- •VII. Элементы теории вероятностей. Случайные события
- •Вопросы для самопроверки:
Вопросы для самопроверки:
Какая функция называется бесконечно малой?
Какова связь между бесконечно малой и бесконечно большой функциями?
Сформулируйте основные теоремы о пределах.
Дайте определение непрерывной функции в точке и на промежутке (а;в).
Тема 3. Дифференциальное исчисление
Полезно выписать производные основных элементарных функций для случая, когда аргумент этих функций U есть в свою очередь функция от независимой переменной х, т.е. U=U(x):
 ,
,
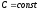 ;
2.
;
2.
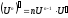 ,
,
3.
 ;
4.
;
4.
 ;
5.
;
5. ;
;
6.
 ;
7.
;
7. ;
;
8.
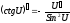 ;
9.
;
9. ;
;
10.
 ;
; 11.
11.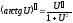 ;
;
12.
 ;
13.
;
13.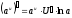 ;
;
14.
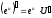 ;
15.
;
15. ;
16.
;
16. ;
;
Данные
производные позволяют дифференцировать
всякую сложную функцию, которая
представляет собой цепочку основных
элементарных функций. Если
 ,
то
,
то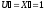 и вышеприведенный перечень упрощается:
и вышеприведенный перечень упрощается:
1.
 ,
, ;
;
2.
 ,
, ;
;
3.
 ;
и т.д.
;
и т.д.
Задача
1.
Найти производную функции
 .
.
Решение:


Задача
2.
Найти
 .
.
Решение:
 Тогда
Тогда .
.
Если
известна производная
 функции
функции ,
то дифференциал функции может быть
легко вычислен по формуле:
,
то дифференциал функции может быть
легко вычислен по формуле: .
.
Решение:
Найдем производную
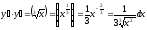 .
.
Вопросы для самопроверки:
Дайте определение производной функции. Найдите производную функции
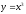 с помощью определения производной.
с помощью определения производной.Геометрический смысл производной функции.
Физический смысл первой и второй производной.
Сформулируйте правила дифференцирования сложных функций.
Чем отличается дифференциал функции от ее приращения?
Тема 4. Приложения дифференциального исчисления
Согласно
правилу Лопиталя, если функции
 и
и одновременно стремится к 0 или
одновременно стремится к 0 или при
при ,
то
,
то .
.
Если
отношение производных функций тоже
имеет вид
 или
или ,
то можно снова применить правило Лопиталя
и так несколько раз до получения
результата.
,
то можно снова применить правило Лопиталя
и так несколько раз до получения
результата.
Задача
1.
Найти
 .
.
Решение:
При
х, стремящемся к 0, числитель и знаменатель
стремятся также к 0, т.е. имеем
неопределенность вида
 и применимо правило Лопиталя:
и применимо правило Лопиталя:

При х, стремящемся к 0, числитель и знаменатель новой дроби стремятся к 0. По правилу Лопиталя:

По-прежнему
имеем неопределенность вида
 ,
т.к.
,
т.к.
Применяя еще раз правило Лопиталя, получаем:

Для
отыскания экстремумов и промежутков
монотонности функции
 поступаем следующим образом:
поступаем следующим образом:
Находим производную
 .
.Находим точки, в которых
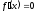 или
или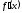 не существует.
не существует.Разбиваем этими точками область определения
 на промежутки.
на промежутки.Методом проб определяем знак
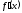 в этих промежутках и находим интервалы
монотонности.
в этих промежутках и находим интервалы
монотонности.Применяем достаточное условие экстремума. Согласно ему точка, в которой
 определена, а
определена, а меняет знак с минуса на плюс, есть точка
минимума. Точка, в которой
меняет знак с минуса на плюс, есть точка
минимума. Точка, в которой определена, а
определена, а меняет знак с плюса на минус, есть точка
максимума.
меняет знак с плюса на минус, есть точка
максимума.
Задача
2.
Найти интервалы монотонности и точки
экстремума функции
 .
.
Решение:
1.
 ;
;
2.
 существует для
существует для .
.
3.
Разбиваем значениями Х= 1
числовую ось Х на промежутки:
1
числовую ось Х на промежутки:

4.
 и, следовательно,
и, следовательно, во всем промежутке
во всем промежутке Функция в этом промежутке возрастает.
Функция в этом промежутке возрастает.
 и,
следовательно,
и,
следовательно,
 во всем промежутке
во всем промежутке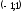 и здесь функция убывает.
и здесь функция убывает.
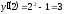 и,
следовательно,
и,
следовательно,
 в промежутке
в промежутке ,
а функция возрастает.
,
а функция возрастает.
5.
Из чертежа следует, что
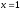 есть точка максимума, а
есть точка максимума, а
 есть точка минимума, а
есть точка минимума, а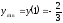 .
.
