- •Слайд №1Тригонометрические функции
- •Слайд№20Выражение тригонометрических функций через одну из них того же аргумента
- •Слайд№23Преобразование суммы тригонометрических функций
- •Слайд№31Обратные тригонометрические функции, их свойства и графики.
- •Слайд№36Определение тригонометрических функций через окружность
- •Слайд№37
- •Слайд№45Литература
- •[Править] Ссылки
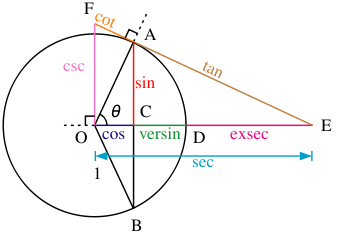
Слайд№36Определение тригонометрических функций через окружность
|
|
Пусть
на плоскости задана прямоугольная
система координат с началом в точке
O и с осями OX и OY. Возьмём в этой системе
координат окружность с центром в точке
O и радиусом, равным единице. Пусть
отрезок OA поворачивается на произвольный
угол
|
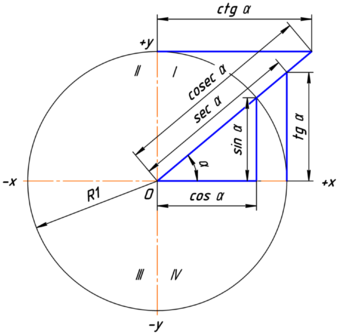
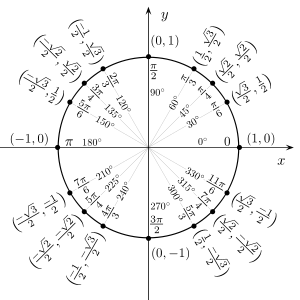
Слайд№37
|
Значения
тригонометрических функций на
окружности.
|
Слайд№38
Определение тригонометрических функций как решений дифференциальных уравнений
Функции косинусисинусможно определить какчётное(косинус) инечётное(синус) решениедифференциального уравнения
![]()
с
начальными условиями
![]() ,
то есть как функций одной переменной,
вторая производная которых равна самой
функции, взятой со знаком минус:
,
то есть как функций одной переменной,
вторая производная которых равна самой
функции, взятой со знаком минус:
![]()
![]()
Слайд№39
[править] Определение тригонометрических функций как решений функциональных уравнений
Функции косинусисинусможно определить какнепрерывные решения(fиgсоответственно) системыфункциональных уравнений:
![]()
[править]
Слайд№40
Определение тригонометрических функций через ряды
Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлораи представить синус и косинус в виде степенны́х рядов:
![]()
![]()
Пользуясь
этими формулами, а также уравнениями
![]()
![]()
![]() и
и![]() можно
найти разложения в ряд Тейлора и других
тригонометрических функций:
можно
найти разложения в ряд Тейлора и других
тригонометрических функций:
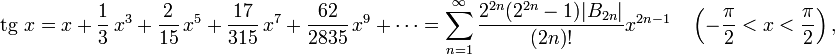
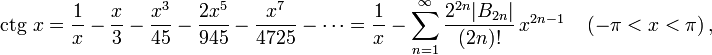
![]()
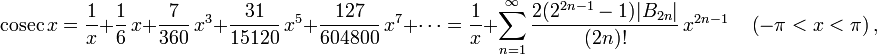
где
![]() —числа
Бернулли,
—числа
Бернулли,
![]() —числа
Эйлера.
—числа
Эйлера.
Слайд№41
Производные и интегралы
Все тригонометрические функции непрерывно и неограниченно дифференцируемы на всей области определения:
![]()
![]()
![]()
![]()
![]()
![]()
Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом:
![]()
![]()
![]()
![]()
![]()
![]()
Слайд№42
[править] Тригонометрические функции комплексного аргумента
[править] Определение
Формула Эйлера:
![]()
позволяет определить тригонометрические функции от комплексных аргументов через экспонентуили (с помощьюрядов) каканалитическое продолжениеих вещественных аналогов:
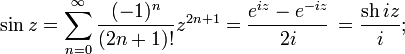
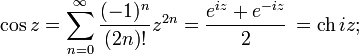
![]()
![]()
![]()
![]() где
где![]()
Соответственно, для вещественного x,
![]()
![]()
Комплексные синус и косинус тесно связаны с гиперболическими функциями:
![]()
![]()
Слайд№43
[править] Комплексные графики
На следующих графиках изображена комплексная плоскость, а значения функций выделены цветом. Яркость отражает абсолютное значение (чёрный — ноль). Цвет изменяется от аргумента и угла согласно карте.
|
Тригонометрические функции в комплексной плоскости | |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[править] Слайд№44
История названий
Тригонометрические функции были введены еще древними греками и определялись, как отношения сторон прямоугольного треугольника. Они считаются функциями от величины угла. Благодаря Тейлору, эти функции могут быть так же представлены в виде суммы степенных рядов.
Тригонометрические функции используются в основном при исследовании периодических процессов.
Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива», то есть половина хорды), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающимтетивуи хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как варабском языкекраткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений налатыньевропейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.
Современные краткие обозначения sinиcosвведеныУильямом Отредоми закреплены в трудахЭйлера.
Термины «тангенс» (от лат.tangens— касающийся) и «секанс» (лат.secans— секущий) были введены датским математикомТомасом Финке(1561—1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583).
Сам термин тригонометрические функциивведёнКлюгелемв1770 году.