Слайд №1Тригонометрические функции

Тригонометрические функции — математические функции от угла. Они важны при изучении геометрии, а также при исследовании периодических процессов. Обычно тригонометрические функции определяют как отношения сторон прямоугольного треугольника или длины определённых отрезков в единичной окружности. В настоящее время выделяют шесть основных тригонометрических функций, указанных ниже вместе с уравнениями, связывающими их друг с другом. Для последних четырёх функций, эти соотношения часто называют определениями этих функций, однако можно определять эти функции геометрически или как-нибудь по-другому. С тригонометрическими функциями тесно связаны обратные им функции.

Слайд №2К тригонометрическим функциям относятся:

прямые тригонометрические функции

• синус (sin x)

• косинус (cos x)

производные тригонометрические функции

• тангенс (tg x)

• котангенс (ctg x)

другие тригонометрические функции

• секанс (sec x)

• косеканс (cosec x)

Слайд №3Свойства тригонометрических функций

Простейшие тождества

Поскольку синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α, то, согласно уравнению единичной окружности или теореме Пифагора, имеем:

Это соотношение называется основным тригонометрическим тождеством.

Деля это уравнение на квадрат косинуса и синуса соответственно имеем далее:

Слайд№4Непрерывность

Синус и косинус — непрерывные функции. Тангенс и секанс имеют точки разрыва котангенс и косеканс —

Слайд№5Чётность

Косинус и секанс — чётные. Остальные четыре функции — нечётные, то есть:

Слайд№6Периодичность

Функции —периодические с периодом 2π, функции и— c периодомπ.

Слайд№7Формулы приведения

Формулами приведения называются формулы следующего вида:

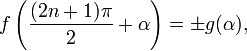
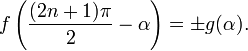
Слайд№8Формулы сложения

Значения тригонометрических функций суммы и разности двух углов:

Аналогичные формулы для суммы трёх углов:

Слайд№9Формулы для кратных углов

Формулы двойного угла:

Слайд№10Формулы тройного угла:

Слайд№11Прочие формулы для кратных углов:

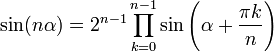следует из формулы дополнения и формулы Гаусса для Гамма-функции.

Слайд№12Из формулы Муавра можно получить следующие общие выражения для кратных углов:

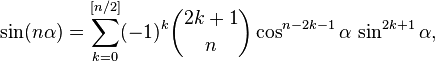
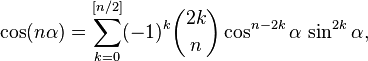
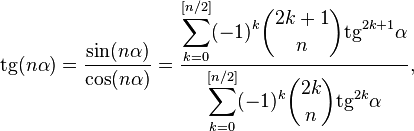
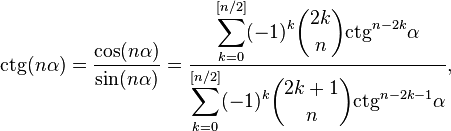
где —целая часть числа ,—биномиальный коэффициент.

Слайд№13Формулы половинного угла:

Слайд№13Произведения

Формулы для произведений функций двух углов:

Слайд№14Аналогичные формулы для произведений синусов и косинусов трёх углов:

Слайд№15Степени

Слайд№16Суммы

Для функций от аргумента существует представление:

где угол находится из соотношений:

Слайд№17Однопараметрическое представление

Все тригонометрические функции можно выразить через тангенс половинного угла.

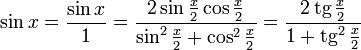
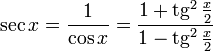
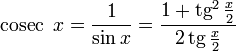
Слайд№18Знаки тригонометрических функций

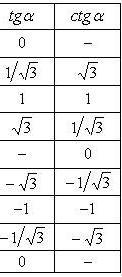
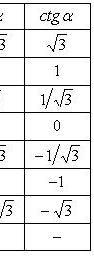
Слайд№19Некоторые значения тригонометрических функций