1.3. Внутренние силы и напряжения

Числовой мерой распределения внутренних сил по сечению является напряжение.

Рассмотрим сечение А некоторого тела (рис. 5). В окрестности точки K выделим элементарную площадку , в пределах которой выявлена внутренняя сила. За среднее напряжение на площадкеAF принимаем отношение

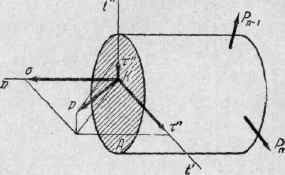
Рис. 5

Будем уменьшать площадку , стягивая ее в точкуК. Поскольку среда непрерывна, возможен предельный переход при .

Векторная величина представляет собой полное напряжение в точ­ке К в сечении А. Напряжение имеет размерность силы, деленной на площадь

Полное напряжение может быть разложено на три составляю­щие по нормали к плоскости сечения и по двум осям в плоскости сечения (рис. 5). Проекция вектора полного напряжения на нормаль обозначается через и называетсянормальным напряжением. Со­ставляющие в плоскости сечения называются касательными напря­жениями и обозначаются через . В зависимости от расположения и наименования осей обозначения и снабжаются системой ин­дексов, порядок которых будет установлен в дальнейшем.

Сово­купность напряжений для множества площадок, проходящих через точку, образует напряженное состояние в точке, которое опреде­ляется шестью числовыми величинами и является в сопротивлении материалов одним из наиболее важных понятий.

1.4. Перемещения и деформации

При нагружении тел внешними силами или при изменении температуры происходит их деформация. При деформи­ровании тела его точки, а также мысленно проведенные линии или сечения перемещаются в плоскости или в пространстве относи­тельно своего исходного положения.

Под нагрузкой в твердом теле возникают внутренние силы взаимодействия между частицами, оказывающие противодействие внешним силам и стремящиеся вернуть частицы тела в положение, которое те занимали до деформации.

Деформации бывают упругие, т. е. исчезающие после прекраще­ния действия вызвавших их сил, и пластические, или остаточные,— не исчезающие.

С увеличением внешних сил внутренние силы также увеличи­ваются до известного предела, зависящего от свойств ма­териала. Наступает момент, когда тело уже не в состоянии сопро­тивляться дальнейшему увеличению внешних сил. Тогда оно раз­рушается. В большинстве случаев для величины деформаций эле­ментов конструкции устанавливают определенные ограничения.

В сопротивлении материалов изучают следующие основные виды деформаций стержня: растяжение и сжатие, сдвиг (срез), кручение и изгиб и более сложные деформации, получаю­щиеся в результате сочетания нескольких основных.

Основным объектом, рассматриваемым в сопротивлении матери­алов, является стержень с прямолинейной осью.

Растяжение или сжатие возникает, например, в случае, когда к стержню по его оси приложены противоположно направленные силы (рис. 6). При этом про­исходит перемещение сечений вдоль оси стержня, который при растяжении удлиняется, а при сжатии укорачивается.

Рис. 6

Изменение первоначальной длиныl стержня называют абсолютным удлинением при растяжении или абсолютным укорочением при сжатии. От­ношение абсолютного удлинения (укорочения) к первоначальной длине стержня называют средним относительным удлинением на длине и обозначают обычно буквой е_ср:

На растяжение или сжатие работают многие элементы конструк­ций: стержни ферм, колонны, штоки паровых машин и поршневых насосов, стяжные винты и другие детали.

Сдвиг (срез) возникает, когда внешние силы смещают два па­раллельных плоских сечения стержня одно относительно другого при неизменном расстоянии между ними (рис. 7).

Рис 7.

Величина сме­щения называется абсолютным сдвигом.

Относительным сдвигом называют отношение абсолютного сдвига к расстоянию а между смещающимися плоскостями (тангенс угла ). Вследствие малости угла при упругих деформациях его тангенс принимают равным углу перекоса рассматриваемого элемента. Следовательно, относитель­ный сдвиг

Относительный сдвиг является угловой деформацией, характери­зующей перекос элемента. На сдвиг или срез работают, например, заклепки и болты, скрепляющие элементы, которые внешние силы стремятся сдвинуть один относительно другого.

Кручение возникает при действии на стержень внешних сил, об­разующих момент относительно оси стержня (рис. 8).

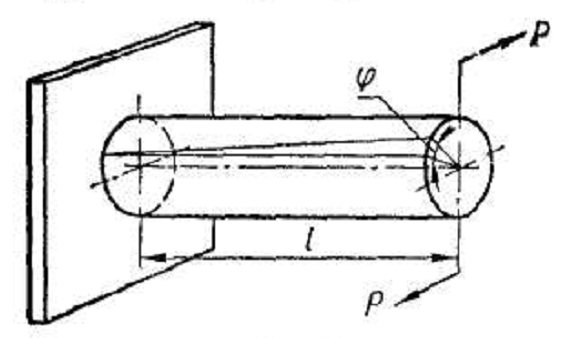
Рис 8

Деформация кручения сопровождается поворотом поперечных сечений стержня относительно друг друга вокруг его оси. Угол поворота одного се­чения стержня относительно другого, находящегося на расстоянии l, называют углом закручивания на длине l.

Oтносительным углом закручи­вания называют отношение угла за­кручивания к длинеl

На кручение работают валы, шпин­дели токарных и сверлильных стан­ков и другие детали.

Деформация изгиба (рис. 9) заключается в искривлении оси прямого или кривого стержня.

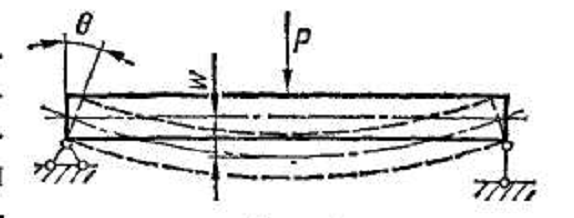
Рис 9.

Происходящее при этом перемещение какой-либо точки оси стерж­ня выражается вектором, начало которого совмещено с первона­чальным положением точки, а конец — с положением той же точки в деформированном стержне. В прямых стержнях перемещения то­чек, направленные перпендикулярно к начальному положению оси, называют прогибами и обозначают буквой w. При изгибе происхо­дит также поворот сечений стержня вокруг осей, лежащих в плос­костях сечений. Углы поворота сечений относительно их начальных положений обозначаются буквой .

На изгиб работают, например, оси железнодорожных вагонов, листовые рессоры, зубья шестерен, спицы колес, балки междуэтажных перекрытий, рычаги и многие другие детали.

В результате одновременного дей­ствия на тело сил, вызывающих раз­личные виды указанных основных де­формаций, возникает более сложная деформация.

Для определения деформации в какой-либо точке A (рис. 10) проведем в недеформированном теле отрезок прямой АВ, исходя­щий из этой точки в произвольном направлении и имеющий длину S

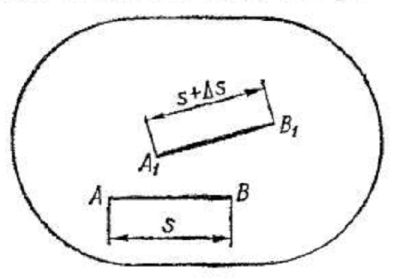
Рис. 10

После деформации точки А и В переместятся и займут положения и соответственно, а расстояние S между ними изменится на величину . Отношение

называется средней относительной линейной деформацией отрезка АВ. Приближая точку В к точ­ке A, т. е. уменьшая длину отрезка s, в пределе получим

Величина представляет собой относительную линейную де­формацию в точке А по направлению АВ. Если , то рас­стояние между точкамиА и В увели­чивается, (относитель­ным удлинении), при наблюдается относительным уко­рочение.

В точке А относи­тельные линейные деформации по раз­личным направлениям могут быть различны. В выбранной прямоуголь­ной системы координат ОХУZ относительные линейные деформа­ции в точке A обозначают соответственно через .

Для полной характеристики деформации в точке вводят еще и угловые деформации. Если до деформации тела из точки А (рис. 11) провести два отрезка АВ и AС, образующих прямой угол, то после перемещения точек вследствие дефор­мации тела отрезки займут положения и а угол между ними изме­нитсяна величину .

Приближая точки В и С к точке А, в пределе получим изменение первона­чально прямого угла на величину

Это изменение прямого угла, выра­женное в радианах, называется

относительной угловой деформаци­ей в точке А в плоскости, где лежат отрезки

АВ и АС. В точке А относительные угловые деформации в трех взаимно перпендикулярных координатных плоско­стях различны и обозначаюся соответственно -

Рис. 11

Деформированное состояние в точке тела полностью определяет­ся шестью компонентами деформации — тремя относительными ли­нейными деформациями и тремя относительными угло­выми деформациями .