Лекция 2 Геометрический метод решения злп с двумя переменными.

1. Геометрический смысл злп с двумя переменными

Рассмотрим ЗЛП в стандартной форме при условии, что ее система ограничений содержит только две переменные. В этом случае задача имеет простой геометрический смысл, и, используя геометрическую интерпретацию, легко найти ее решение.

Система ограничений задачи с двумя переменными в стандартной форме имеет вид:

(1)

(2)

Среди неотрицательных решений системы (1) требуется найти такое решение , при котором линейная функция

(3) принимает наименьшее значение.

Обсуждение этой задачи начнем с рассмотрения одного линейного неравенства . Выберем на плоскости систему координат. Естественно, встает вопрос: какую область на плоскости определяет это неравенство? Ответ на этот вопрос известен из школьного

курса математики. Следует рассмотреть прямую l, определяемую уравнением . Эта прямая разбивает всю плоскость на две полуплоскости (на рис. 3.1 изображен случай). В одной из них выполняется неравенство, а в другой. Саму прямуюl мы считаем принадлежащей каждой из указанных

Рис. 3. 1

полуплоскостей. Практически, для того чтобы узнать, какая из двух полуплоскостей соответствует неравенству , поступают так: если, то приводят неравенство к одному из видовили. В первом случае искомая полуплоскость лежит выше прямойl, во втором – ниже прямой l. Если же , то неравенство приводится к одному из видовили, соответствующая полуплоскость лежит слева или справа от прямой.

Таким образом, первое неравенство системы (1) определяет некоторую полуплоскость , а второе – полуплоскостьи т.д. Если какая-нибудь пара чиселудовлетворяет каждому неравенству системы (1), то точкапринадлежит пересечению полуплоскостей, которое является некоторой многоугольной областью М. Нетрудно заметить, что эта область может быть замкнутой или незамкнутой неограниченной.

Рис. 3. 2 Рис. 3. 3

Штрихи на рис. 3.2 и рис. 3.3 указывают, с какой стороны от прямой лежит полуплоскость, соответствующая заданному неравенству.

Область М называют областью решений системы (1). Так как граница области М состоит из отрезков прямых, то М является многоугольной областью; если область М ограничена, то ее называют многоугольником решений системы (1). Может случиться, что , в этом случае система (1) несовместна. Заметим, что если добавить условие (2), то область решений вся будет находиться в первой четверти.

Область решений М обладает очень важным свойством: она является выпуклой. Фигура называется выпуклой, если она вместе с любыми двумя своими точками A и B содержит и весь отрезок АВ.

Рис. 3. 4 Рис. 3. 5

Выпуклая область Невыпуклая область

Из геометрии известно, что точка С=принадлежит отрезкуAB, где A=,B=, тогда и только тогда, когда выполняются равенства (4):

(4) , .

Условие (4) можно записать короче в виде (5):

(5) С = A + B, .

Если =0, то = 1 и C = B, если = 1, то = 0 и C = A.

Известно, что полуплоскость – выпуклая фигура, пересечение выпуклых фигур – также выпуклая фигура, поэтому область решений системы неравенств (1) и (2) является выпуклой.

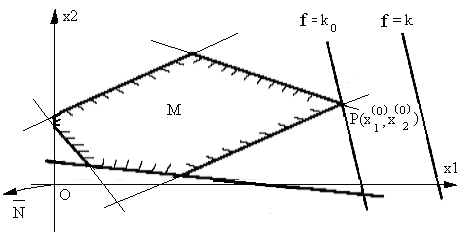
Рис. 3. 6

Итак, область решений системы неравенств (1) и (2) есть выпуклая многоугольная область, которая получается в результате пересечения всех полуплоскостей, соответствующих неравенствам системы (1), с первой четвертью.

Изобразим теперь на плоскости множество точек, в которых функция принимает одно и то же значение:. Ясно, что это множество точек прямой. Эту прямую называют прямой (линией) уровня функции, отвечающей значению. Векторперпендикулярен прямой.

Множество точек плоскости, в которых функция принимает значение, где, представляет собой другую прямую уровня, которая параллельна прямой. Изменяяотдо, мы будем перемещать прямую уровня параллельно самой себе, «зачерчивая» всю плоскость. Из геометрии известно, что вектор(градиент функции) показывает направление смещения линии уровняпри измененииотдо.

При этом смещении наступит такой момент, когда при некотором значении линия уровня коснется области М хотя бы в одной точке. Пустьбудет одной из первых точек прикосновения линии уровня с областью М. Тогда пара чисели будет оптимальным решением ЗЛП (1), (2), (3), иmin.

Если область М – неограниченная, то может оказаться, что первой точки прикосновения линии уровня функции , соответствующей наименьшему уровню, с областью М нет. В этом случае задача не имеет оптимального решения (min).

Прямая, которая имеет с областью М по крайней мере одну общую точку и вся область М лежит по одну сторону от этой прямой, называется опорной по отношению к этой области.

Исходная задача на геометрическом языке теперь может быть сформулирована так: среди прямых уровня функции найти такую опорную прямую по отношению к области М, чтобы вся область лежала со стороны больших значений функции. Любая из общих точек этой прямой с областью М даст оптимальное решение задачи. Если область М ограниченная (выпуклый многоугольник), то среди линий уровня две являются опорными для М; из этих двух нужно выбрать ту, которая отвечает меньшему значению.