
- •Глава 10. Нелинейные электрические цепи переменного тока
- •10.1. Общая характеристика нелинейных цепей переменного тока
- •10.2. Реактивная катушка с сердечником из ферромагнитного материала
- •10.3. Потери в сердечниках из ферромагнитного материала
- •10.3.1. Потери на вихревые токи.
- •10.3.2. Потери на гистерезис
- •10.3.3. Разделение потерь на вихревые токи и гистерезис
- •10.4. Форма кривой тока в катушке с ферромагнитным сердечником
- •10.5. Векторная диаграмма и эквивалентная схема реактивной катушки с ферромагнитным сердечником
- •10.6. Феррорезонанс напряжений
- •10.7. Ферромагнитный стабилизатор напряжения
- •10.8. Ферромагнитный усилитель мощности
- •10.9 Выпрямление переменных токов
10.9 Выпрямление переменных токов
Для выпрямления, т.е. для преобразования переменного тока в постоянный, применяются нелинейные сопротивления с несимметричными вольтамперными характеристиками, имеющие одностороннюю проводимость. Таким свойством обладают германиевые, кремниевые и другие полупроводниковые вентили, ртутные выпрямители, газотроны и электронные лампы.
На рис. 10.17,а изображена типичная ВАХ полупроводникового вентиля и характеристика идеального вентиля (рис. 10.17,б),
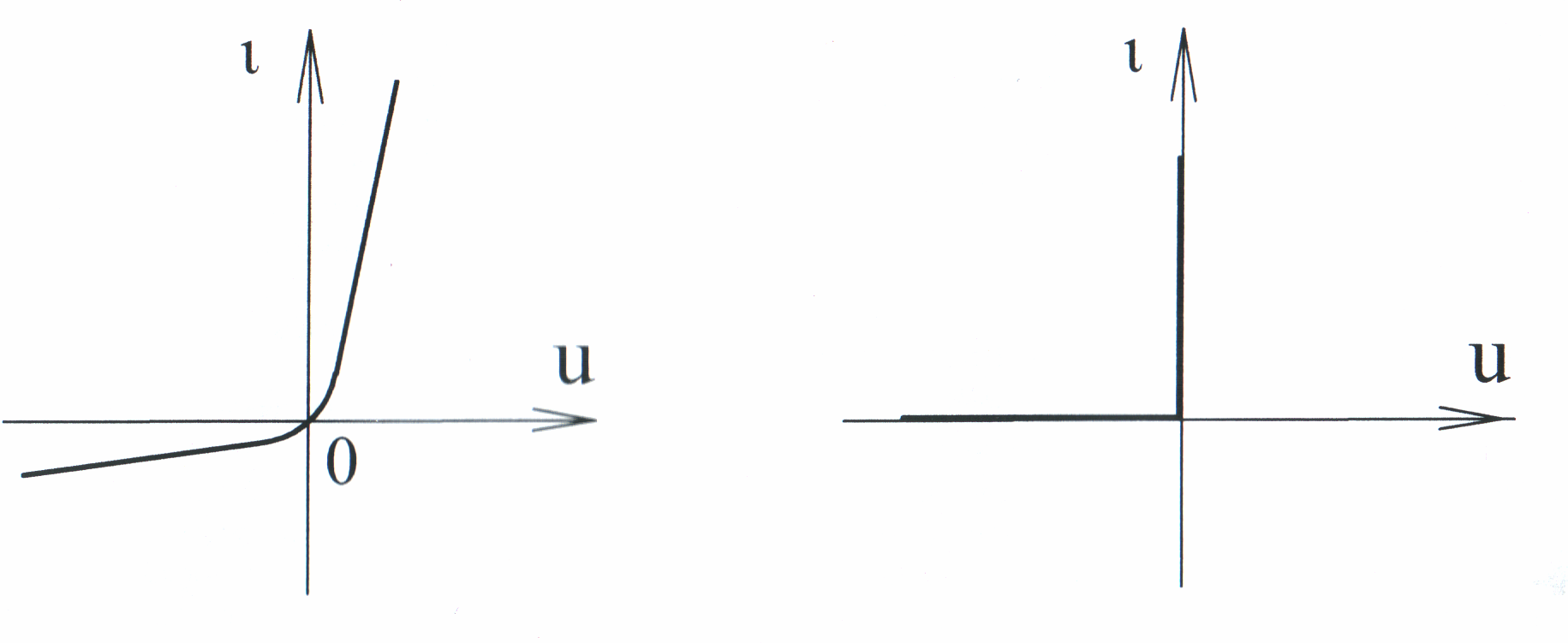
а) б)
Рис. 10.17
сопротивление которого равно нулю для прямого направления тока и – для обратного.
Е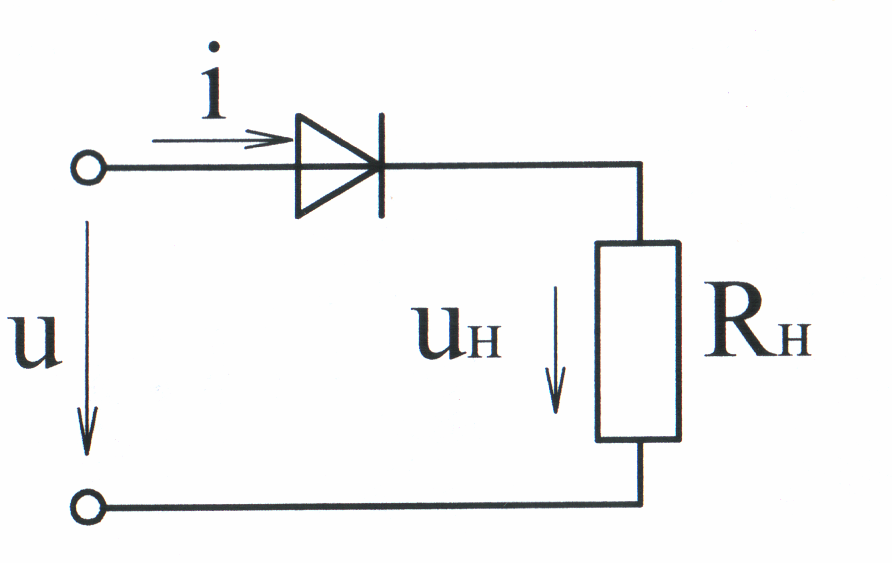 сли
включить идеальный вентиль последовательно
с нагрузкой, имеющей активное сопротивление
(рис. 10.18), то для прямого полупериода
напряжения
сли
включить идеальный вентиль последовательно
с нагрузкой, имеющей активное сопротивление
(рис. 10.18), то для прямого полупериода
напряжения
![]() ток
ток
![]()
Рис. 10.18
![]() а для обратного полупериода
а для обратного полупериода
![]() так как сопротивление
вентиля для
так как сопротивление
вентиля для
обратного направления тока равно , т.е. по цепи идет ток одного направления (рис. 10.19). Рассмотренное выпрямление называется
о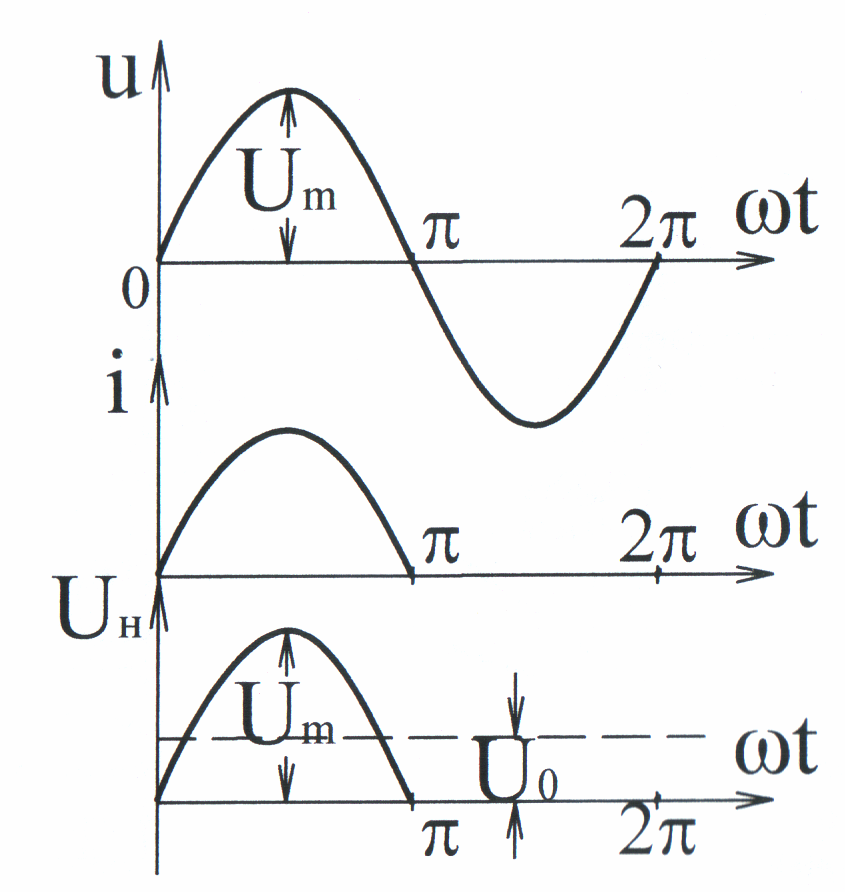 днополупериодным.
Напряжение на нагрузке
днополупериодным.
Напряжение на нагрузке
![]() резко несинусоидально и имеет наряду
с постоянной составляющей
резко несинусоидально и имеет наряду
с постоянной составляющей
![]() еще первую и все четные гармоники:
еще первую и все четные гармоники:
![]()

![]()
![]() (10.30)
(10.30)
Рис. 10.19 Рассмотрим, каковы будут значения тока,
напряжения и мощности источника и
приемника при отсутствии фильтра.
Действующее
значение напряжения источника
![]() ,
т.е. остается тем же, что и при отсутствии
выпрямителя.
,
т.е. остается тем же, что и при отсутствии
выпрямителя.
Ток источника и приемника:
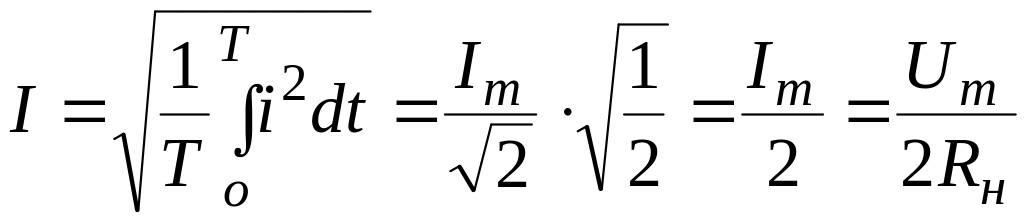 ,
,
т.е. действующее значение тока зависит от напряжения источника по линейному закону
Напряжение на нагрузке
![]() .
.
Активная мощность нагрузки и источника
![]() ,
,
т.е. в 2 раза меньше мощности выделяемой при отсутствии выпрямителя.
Полная мощность источника
![]() .
.
Коэффициент мощности источника
![]() (не равен 1,0).
(не равен 1,0).
Это объясняется в рассматриваемом случае не наличием реактивного сопротивления, а искажением формы кривой тока по отношению к форме кривой напряжения источника.
Коэффициент мощности нагрузки
![]()
![]() ;
;
![]()
(В данном случае кривые тока и напряжения по форме одинаковы).
Для осуществления двухполупериодного выпрямления применяется мостовая схема (рис. 10.20) из четырех вентилей. На рис. 10.21 изображены кривые напряжений и тока при этом выпрямлении. Разложение кривой напряжения на нагрузке в ряд Фурье дает:
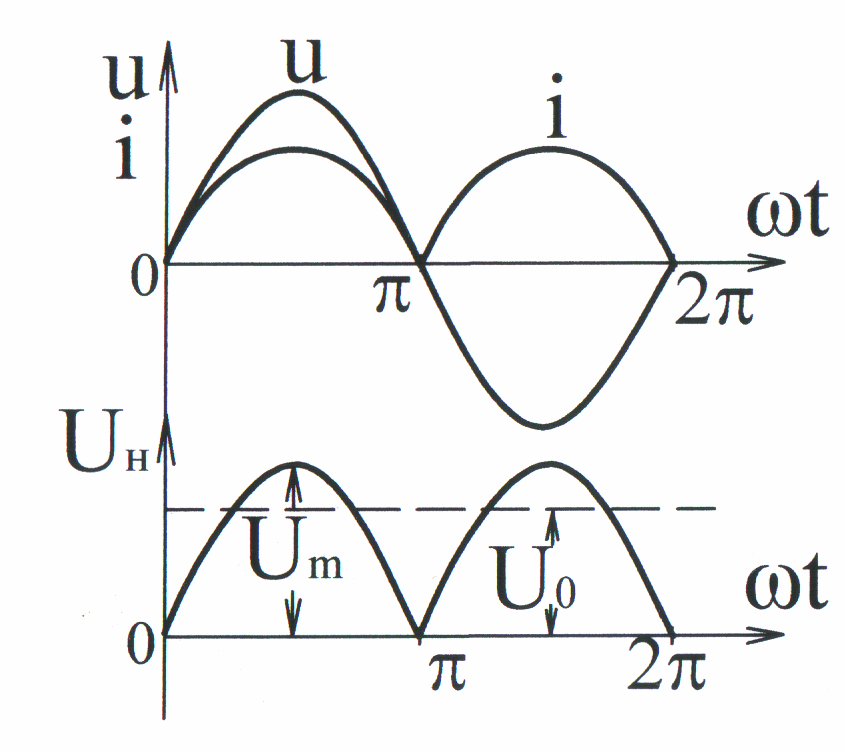
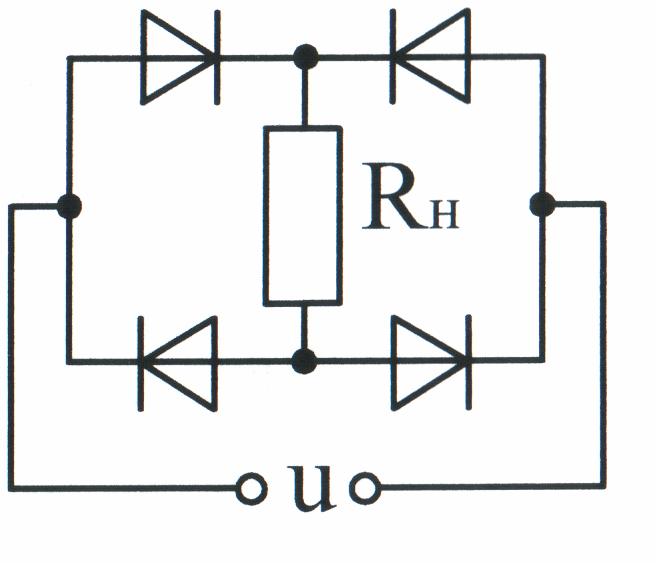
Рис. 10.20 Рис. 10.21
![]()
![]() (10.31)
(10.31)
т.е. при двухполупериодном выпрямлении постоянная составляющая напряжения в 2 раза больше чем при однополупериодном.
Пример 10.1.
Разделить
потери на гистерезис и на вихревые токи
в сердечнике трансформатора, собранном
из плоских листов (толщина 0,5 мм)
высоколегированной стали Э41, если
известно, что при частоте
![]() Гц потери в сердечнике
Гц потери в сердечнике
![]() Вт/кг и при
Вт/кг и при
![]() Гц
Гц
![]() Вт/кг. Определить также потери на вихревые
токи и гистерезис и
Вт/кг. Определить также потери на вихревые
токи и гистерезис и
![]() при частоте
при частоте
![]() Гц.
Гц.
Магнитная индукция в сердечнике Вm остается во всех случаях одной и той же.
Р е ш е н и е. Разделение потерь произведем аналитическим способом. Составляем два уравнения (10.15):
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
В результате решения системы уравнений находим постоянные коэффициенты А и С:
![]() ;
;
![]() .
.
Потери при частоте Гц:
![]() Вт/кг;
Вт/кг;
![]() Вт/кг;
Вт/кг;
![]() Вт/кг.
Вт/кг.
Потери при частоте Гц:
![]() Вт/кг;
Вт/кг;
![]() Вт/кг;
Вт/кг;
![]() Вт/кг.
Вт/кг.
Потери при частоте Гц:
![]() Вт/кг;
Вт/кг;
![]() Вт/кг;
Вт/кг;
![]() Вт/кг.
Вт/кг.
Пример 10.2.
Построить
векторную диаграмму для реактивной
катушки с сердечником из электротехнической
стали, если приложенное к ее зажимам
напряжение
![]() ,
ток в обмотке I
= 10 А и мощность, потребляемая катушкой
P
= 200 Вт.
Активное сопротивление обмотки
,
ток в обмотке I
= 10 А и мощность, потребляемая катушкой
P
= 200 Вт.
Активное сопротивление обмотки
![]() Ом и реактивное сопротивление, учитывающее
поток рассеяния
Ом и реактивное сопротивление, учитывающее
поток рассеяния
![]() Ом. Определить коэффициент мощности
катушки, намагничивающий ток
Ом. Определить коэффициент мощности
катушки, намагничивающий ток
![]() ,
составляющую напряжения
,
уравновешивающую ЭДС, индуктируемую в
обмотке потоком
,
составляющую напряжения
,
уравновешивающую ЭДС, индуктируемую в
обмотке потоком
![]() ,
замыкающимся по сердечнику.
,
замыкающимся по сердечнику.
Примечание. При построении диаграммы предполагать ток изменяющийся по синусоидальному закону, т.е. рассматривать эквивалентную синусоиду тока.
Р е ш е н и е. По заданному напряжению записываем комплексное напряжение
![]() В.
В.
Чтобы записать комплекс тока, определяем коэффициент мощности
![]() ;
;
![]()
Начальную фазу тока определим из выражения:
![]() ;
;
![]()
Комплекс тока
![]() ,
А.
,
А.
Для эквивалентной схемы (рис. 10.8) имеем (по второму закону Кирхгофа в комплексной форме):
![]()
![]()
![]() В.
В.
Таким образом,
![]() В,
В,
![]()
Потери мощности в обмотке:
![]() Вт.
Вт.
Потери мощности в сердечнике:
![]() Вт.
Вт.
Активное сопротивление, учитывающее потери мощности в сердечнике (по формуле 10,23):
![]() Ом.
Ом.
Активная составляющая тока в катушке:
![]() А.
А.
Амплитуда основного потокосцепления:
![]()
 Вб.
Вб.
Реактивная составляющая тока (намагничивающий ток):
![]()
![]() А.
А.
Индуктивность катушки, обусловленная основным потоком:
![]()
![]() Гн = 28,69 мГн.
Гн = 28,69 мГн.
![]()
Рис. 10.22
![]() Ом.
Ом.
Определим угол
потерь
![]() (угол между основным потоком и током):
(угол между основным потоком и током):
![]() ;
;
![]()
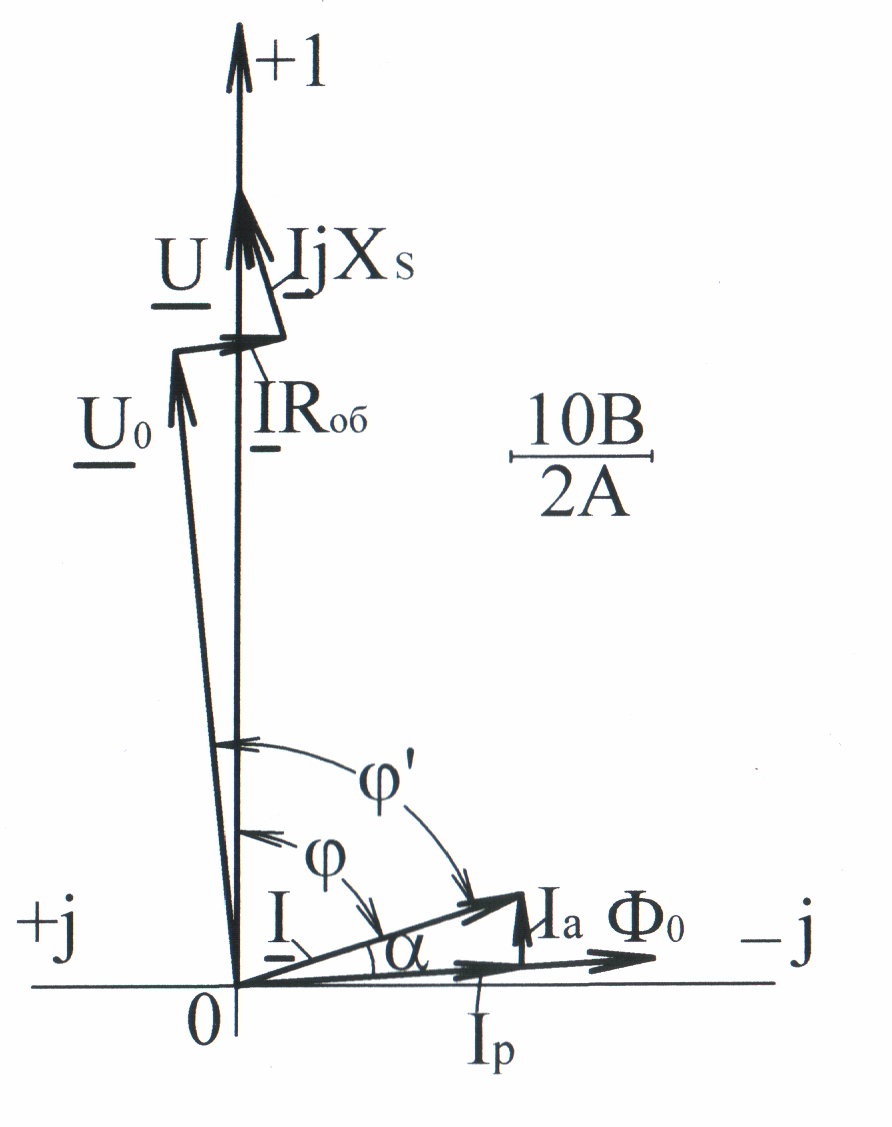
Угол между векторами и
![]()
По результатам расчета на рис. 10.22 построена векторная диаграмма токов и напряжений катушки с ферромагнитным сердечником в координатах комплексной плоскости.
