Биофизика / Специальна Биофизика / Вечканов Е.М., Внуков В.В. Термодинамика и кинетика биологических процессов

Парадокс разрешается, если рассмотреть замкнутую систему, включающую в себя демона Максвелла и сосуд. Для функционирования демона Максвелла необходима передача ему энергии от стороннего источника. За счѐт этой энергии и производится разделение горячих и холодных молекул в сосуде, то есть переход в состояние с меньшей энтропией. С развитием теории информации было установлено, что процесс измерения может не приводить к увеличению энтропии при условии, что он является термодинамически обратимым. Однако в этом случае демон должен запоминать результаты измерения скоростей (стирание их из памяти демона делает процесс необратимым). Поскольку память конечна, в определенный момент демон вынужден стирать старые результаты, что и приводит в конечном итоге к увеличению энтропии всей системы в целом.

§ 16 Понятие градиента

Градиент (grad) какого-либо параметра системы представляет собой отношение разности величин ∆Ф этого параметра в двух точках к расстоянию ∆х между ними (18), (рис. 10):

grad = ∆Ф / ∆ х (18)

Рис. 10 Понятие градиента Биологические системы характеризуются наличием большого количества

градиентов (осмотический, электрический, концентрационный) (рис. 11) Биологическая система способна совершать работу, если в ней имеется градиент. Таким образом градиент является своеобразным депо энергии. Связь свободной энергии и градиента представлена в формуле (19)

F = R T ln Ф1/Ф2 (19)

где F - свободная энергия, R – газовая постоянная, Ф - значение термодинамических параметров в 1 и 2 точках

Совершение работы в системе связано с реализацией свободной энергии. Если совершается работа, то градиент, за счет энергии которого это происходит, уменьшается, но параллельно возникает другой градиент противоположной

21

направленности. При необратимых процессах величина второго градиента будет меньше, чем величина первого.

Рис. 11 Виды градиентов

§17 Электрохимический потенциал

Вфизико-химических системах изменение свободной энергии обычно описывают через изменение электрохимического потенциала μ (20) :

ΔG = mΔμ (20)

где m — количество вещества (моли) в системе.

Изменение электрохимического потенциала при переходе системы из состояния 1 в состояние 2 определяется изменением химической, осмотической и электрической энергий (21)

в) преодолеть силы электрического отталкивания, возникающие при наличии

разности потенциалов (φ2-φ1) между растворами (слагаемое zF (φ2-φ1)).

22

Пример: Измерим величину электрохимического потенциала при переносе ионов Na через мембрану нервной клетки. Этот процесс совершается ферментом Na+, К+-АТФ-азой и обеспечивается энергией гидролиза АТФ. Ион натрия при этом переносится из клетки наружу. Концентрация Na+ внутри клеток (c1) равна 0,015 моль/л, а снаружи (с2) — 0,15 моль/л. Осмотическая работа на каждый моль перенесенного иона равна при 37°С RTln (0,15/0,015) = 5,9 кДж/моль. Внутри клетки электрический потенциал составляет φ1 = –60 мВ, если принять наружный потенциал φ2 = 0. Электрическая работа составляет:

zFΔφ = 9,65 × 104 Кл/моль * 60 * 10-3 В = 5,8 кДж/моль.

Так как с Na+ при его переносе через мембрану в конечном счете не происходит никаких химических превращений и он оказывается примерно в таком же водном окружении, что и раньше, то Δμ0 = 0. Отсюда по уравнению (10) находим Δμ = 0 + 5,9 + 5,8 = 11,7 кДж/моль.

§ 18 Потоки и их взаимодействие вблизи термодинамического равновесия. Соотношение взаимности

Онсагера

Соотношение взаимности Онсагера одна из основных теорем термодинамики неравновесных процессов, которое было установлено в 1931 г. Ларсом Онсагером. В термодинамических системах, в которых имеются градиенты температуры, концентраций компонентов, химических потенциалов, возникают необратимые процессы, связанные с теплопроводностью, диффузией, протеканием химических реакций. Эти процессы характеризуются тепловыми и диффузионными потоками, скоростями химических реакций и т.д. Они называются общим термином «потоки» и обозначаются (Ji), а вызывающие их причины (отклонения термодинамических параметров от равновесных значений)

- термодинамическими силами (Хк). Связь между потоками Ji и силами Хk,

если термодинамические силы малы, записывают в виде линейных уравнений

(22):

уравнениями, a Lik — феноменологическим коэффициентом. Значения Lik рассчитывают или находят опытным путѐм.

23

В случае взаимодействия потоков при перекрѐстных процессах, уравнения взаимности Онсагера, устанавливают связь между кинетическими коэффициентами. Ниже приведены уравнения Онсагера для двух потоков и сил

(23, 24):

В случае когда переходит перенос массы в потоке, уравнение принимает вид

(25):

dm/dt = - D dc/dx (25)

где D – коэффициент диффузии, dc/dx – градиент диффузии, dm/dt – массоперенос, или скорость диффузии.

§ 19 Биологическое значение сопряжения потоков. Коэффициент сопряжения

Энергетический обмен у живых организмов организован таким образом, что они могут обходить энтропийный термодинамический критерий и в них протекают не только возможные, но и невозможные с термодинамической точки зрения реакции. Это все реакции, при которых энтропия уменьшается, а свободная энергия увеличивается, - биосинтез различных веществ, работа систем активного транспорта и т.д. Это оказывается возможным благодаря механизму так называемого энергетического сопряжения. Суть этого сопряжения состоит в том, что возможная с точки зрения энтропийного критерия реакция сопрягается с реакцией термодинамически невозможной и дает для нее энергию.

Два условия необходимы для осуществления энергетического сопряжения:

1)Свободная энергия, даваемая термодинамически возможной реакцией, должна превышать энергию, потребляемую реакцией термодинамически невозможной, то есть должен быть некоторый избыток энергии с учетом вероятных потерь при ее передаче

2)Обе сопрягаемые реакции должны иметь общий компонент. Такими компонентами в биологических системах могут быть фосфат, электрохимический градиент протона и др.

24

Энергетическое сопряжение в биосистемах - это выдающееся изобретение природы. Оно осуществляется обычно при участии структурных элементов клетки. Наиболее ярким примером такого сопряжения являются процессы окислительного и фотосинтетического фосфорилирования, протекающие при участии соответственно сопрягающих митохондриальных и фотосинтетических мембран. В биологических системах сопряжены множество процессов: перенос растворимых веществ и воды, сопряжены многие биохимические процессы. Примером сопряжѐнных биохимических реакций может служить фосфорилирование глюкозы на первой стадии гликолиза (рис. 12).

Рис. 12 Схема сопряжения химических реакций

В живой клетке протекает множество реакций, которые сопровождаются увеличением свободной энергии ( G > 0). Например фосфорилирование глюкозы при гликолизе по схеме:

глюкоза + Ф → глюкозо-6-фосфат + Н2О с G = 13,4 кДж/моль

Этот процесс не может идти самопроизвольно, он протекают за счет сопряжения с другой химической реакцией, изменение свободной энергии которой отрицательно, например с реакцией гидролиза АТФ по уравнению:

АТФ + Н2O → АТФ + Ф с G = –30,5 кДж/моль

Объединив первую и последнюю реакции, можно записать:

АТФ + глюкоза → АДФ + глюкозо-6-фосфат

Складывая изменения свободной энергии реакций при их совместном протекании, получаем для фосфорилирования глюкозы с участием АТФ: G = –30,5 кДж/моль + 13,4 кДж/моль = –17,1 кДж/моль. Этот пример иллюстрирует основной способ преобразования энергии в клетке: химическая работа совершается путем подключения к реакции с «неблагоприятным» изменением свободной энергии реакций с большим отрицательным изменением свободной энергии. Для того,

25

чтобы осуществлять такое «сопряжение» процессов, клетке пришлось создать в ходе эволюции специальные молекулярные «энергопреобразующие» устройства, которые представляют собой ферментные комплексы, как правило, связанные с мембранами.

Степень сопряжения потоков различная. Для характеристики степени сопряжения вводится коэффициент сопряжения (26).

Q = L12 / (26)

Коэффициент сопряжения колеблется между 0 и 1. Если потоки не сопрягаются q → 0, в случае максимального сопряжения потоков, когда L12 = L11 = L22, то q → 1.

§ 20 Классификация видов энергии

Бриллюэн создал классификацию видов энергии по способности вида энергии превращаться в другие виды энергии. Энтропия служит своеобразной мерой «качества энергии»: чем больше изменение энтропии в процессе преобразования данной энергии в работу, тем ниже еѐ качество. Иными словами: еѐ преобразование в работу происходит с большими потерями. По этому критерию различные формы энергии образуют следующий ряд (рис. 13):

1.Максимально эффективная, превращается во все другие виды энергии.

Гравитационная, ядерная, световая, электрическая

2.Химическая

3.Тепловая.

Деградация высших типов энергии в энергию низших типов – основное эволюционное свойство изолированных систем.

Рис. 13 Классификация видов энергии по Бриллюену

26

§ 21 Диссипативная функция

Диссипативная́ функция (функция рассеяния) — функция, вводимая для учѐта перехода энергии упорядоченного движения в энергию неупорядоченного движения, в конечном счѐте — в тепловую. Таким образом

диссипативная функция отражает скорость продуцирования энтропии. Диссипативная функция, делѐнная на абсолютную температуру, определяет скорость, с которой возрастает энтропия в системе (27).

β (σ) = T * diS/dt = (27)

где T – абсолютная температура, diS/dt – скорость продукции энтропии внутри системы, Xi – градиенты, Ii –скорости потоков.

Функция диссипации для химических процессов будет иметь вид (28):

β (хим) = (28)

где Аk – сила, вызывающая химическое преобразование, Vk – скорость всех сопряжѐнных реакций.

Стационарное состояние может быть устойчивым и неустойчивым. Функция диссипации используется в качестве критерия устойчивости стационарного состояния (рис.14).

Рис. 14 Иллюстрация диссипативной функции, как критерия устойчивого стационарного состояния. Х – сила, вызывающая стационарное состояние Функция диссипации при любом отклонении от устойчивого стационарного

состояния растѐт, при этом сила вызывающая стационарное состояние будет стремиться к одному значению Х`, а функция диссипации (β) к своему минимуму – второе выражение теоремы Пригожина. В случае неустойчивого стационарного состояния, система будет стремиться выйти из него и

27

никогда не возвратиться к исходному состоянию. При этом могут возникать новые стационарные состояния.

§ 22 Диссипативные структуры

Одно из главных достижений И. Р. Пригожина заключалось в том, что он показал существование неравновесных термодинамических систем, которые при определѐнных условиях, поглощая вещество и энергию из окружающего пространства, могут совершать качественный скачок к усложнению (диссипативные структуры). Причѐм такой скачок не может быть предсказан, исходя из классических законов статистики.

Таким образом диссипативная структура это устойчивое состояние, возникающее в неравновесной среде при условии диссипации (рассеивания) энергии, которая поступает извне. Диссипативная система характеризуется спонтанным появлением сложной, зачастую хаотичной структуры. Простыми примерами диссипативных структур являются ячейки Бенара, лазеры, реакция Белоусова — Жаботинского и биологические процессы.

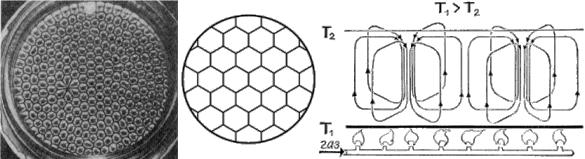
Ячейки Бернара. В 1900 году была опубликована статья французского исследователя Бернара с фотографией структуры, по виду напоминавшей пчелиные соты (рис. 15А). При нагревании снизу слоя ртути, налитой в плоский широкий сосуд, весь слой неожиданно распадался на одинаковые вертикальные шестигранные призмы, которые впоследствии были названы ячейками Бернара (рис. 15Б). В центральной части каждой ячейки жидкость поднимается, а вблизи вертикальных граней опускается. Иными словами, в сосуде возникают направленные потоки, которые поднимают нагретую жидкость (с температурой T1) вверх, а холодную (с температурой T2) опускают вниз (рис. 15В).

Рис. 15 Конвективные ячейки Бернара – пример диссипативной структуры.

28

§ 23 Реакция Белоусова - Жаботинского

Реакция Белоусова - Жаботинского - класс химических реакций, протекающих в колебательном режиме, при котором некоторые параметры реакции (цвет, концентрация компонентов, температура и др.) изменяются периодически, образуя сложную пространственно-временную структуру реакционной среды (рис. 16).

Рис. 16 Колебания окраски раствора при протекании реакции Белоусова – Жаботинского.

Внастоящее время под этим названием объединяется целый класс родственных химических систем, близких по механизму, но различающихся используемыми катализаторами (Ce3+, Mn2+ и комплексы Fe2+, Ru2+), органическими восстановителями (малоновая кислота, броммалоновая кислота, лимонная кислота, яблочная кислота и др.) и окислителями (броматы, иодаты и др.). При определенных условиях эти системы могут демонстрировать очень сложные формы поведения от регулярных периодических до хаотических колебаний и являются важным объектом исследования универсальных закономерностей нелинейных систем.

В1958 г. русский химик Белоусов описал окисление лимонной кислоты броматом калия, катализируемое ионной парой Се4+ - Се3+. Далее изучением данной реакции занялся Жаботинский. Как правило, реакция проводится при 25 0С в сернокислом растворе смеси бромата калия, малоновой и броммалоновой кислот и сернокислого церия. При проведении реакции наблюдаются колебания окраски раствора, вызванные колебаниями концентрации различных ионов церия (рис. 17).

29

Рис. 17 Упрощѐнная схема протекания реакции Белоусова-Жаботинского Распространение химических колебаний в пространстве особенно наглядно,

при проведении реакции в чашке Петри. В чашке образуются причудливые фигуры – концентрические окружности, спирали, «вихри»,распространяющиеся со скоростью 1 мм\мин (рис.18).

Рис. 18 Некоторые конфигурации, возникающие при реакции Белоусова — Жаботинского в тонком слое в чашке Петри

§ 24 Невозможность усложнения организации в области линейной термодинамики

Линейная термодинамика описывает стабильное, предсказуемое поведение систем, стремящихся к минимальному уровню активности, совместимому с питающими их потоками.

За пределами линейной области устойчивость уже не является следствием общих законов физики. В случае неустойчивых состояний флуктуации вместо того, чтобы затухать, усиливаются и завладевают всей системой, вынуждая ее

30