10. Непрерывность функции на отрезке. Свойства функций непрерывных на отрезке.
Непрерывность функции в интервале и на отрезке:
Функция у=ƒ(х) называется непрерывной в интервале (a, b), если она непрерывна в каждой точке этого интервала.
Ф
ункция
у=ƒ(х) называется непрерывной на отрезке
[а, b],
если она непрерывна в интервале (a,
b) и в точке х=а
непрерывна справа (т.е.
), а в точке x=b
непрерывна слева (т. е. ).
Свойства функций непрерывных на отрезке:
Если функция непрерывна на отрезке, то она достигает на этом отрезке свои наибольшее и наименьшее значения (теорема Вейерштрасса).
Непрерывная на отрезке
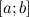функция является ограниченной на этом
отрезке.Если функция
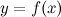является непрерывной на отрезке
и принимает на концах этого отрезка
неравные между собой значения, то есть
,
,
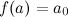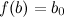то на этом отрезке функция принимает
и все промежуточные значения между
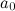и
(теорема Больцано-Коши).
Если функция , которая непрерывна на некотором отрезке , принимает на концах отрезка значения разных знаков, то существует такая точка
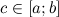такая, что
.
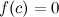<Вернуться назад>
1 1. Точки разрыва и их классификация.
<Вернуться назад>
12. Производная, ее геометрический и механический смысл.
Производная:
Производная равна пределу отношения приращения функции к приращению аргумента, при условии, что последний стремится к нулю:
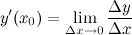
или
Функция, которая имеет конечную производную в некоторой точке, называется дифференцируемой в данной точке. Процесс вычисления производной называется дифференцированием функции.
Геометрический смысл производной:
Производная
функции
,
вычисленная при заданном значении 
,
равна тангенсу угла, образованного
положительным направлением оси 
и
положительным направлением касательной,
проведенной к графику этой функции в
точке с абсциссой
:
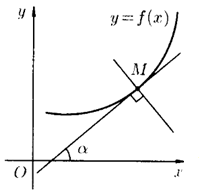
Замечание: Геометрически производная представляет собой угловой коэффициент касательной к графику функции в точке .
Механический смысл производной:
Пусть
задан путь 
движения
материальной точки. Скорость данной
материальной точки в момент времени 
есть
производная от пути 
по
времени
:
<Вернуться назад>
13.Теорема о связи непрерывности и дифференцируемости.
Если функция дифференцируема в точке, то она непрерывна в этой точке.
Доказательство:
Пусть функция у=f(x) дифференцируема в точке х0. Дадим в этой точке аргументу приращение Dх. Функция получит приращение Dу.
Найдем
Следовательно, у=f(x) непрерывна в точке х0.
Следствие. Если х0 – точка разрыва функции, то в ней функция не дифференцируема.
Утверждение, обратное теореме, не верно. Из непрерывности не следует дифференцируемость.
П
ример:
у=|х|, х0=0.
Dх>0, 
;
Dх<0, 
.
В точке х0=0 функция непрерывна, но производной не существует.
<Вернуться назад>
14. Арифметические действия с производными.
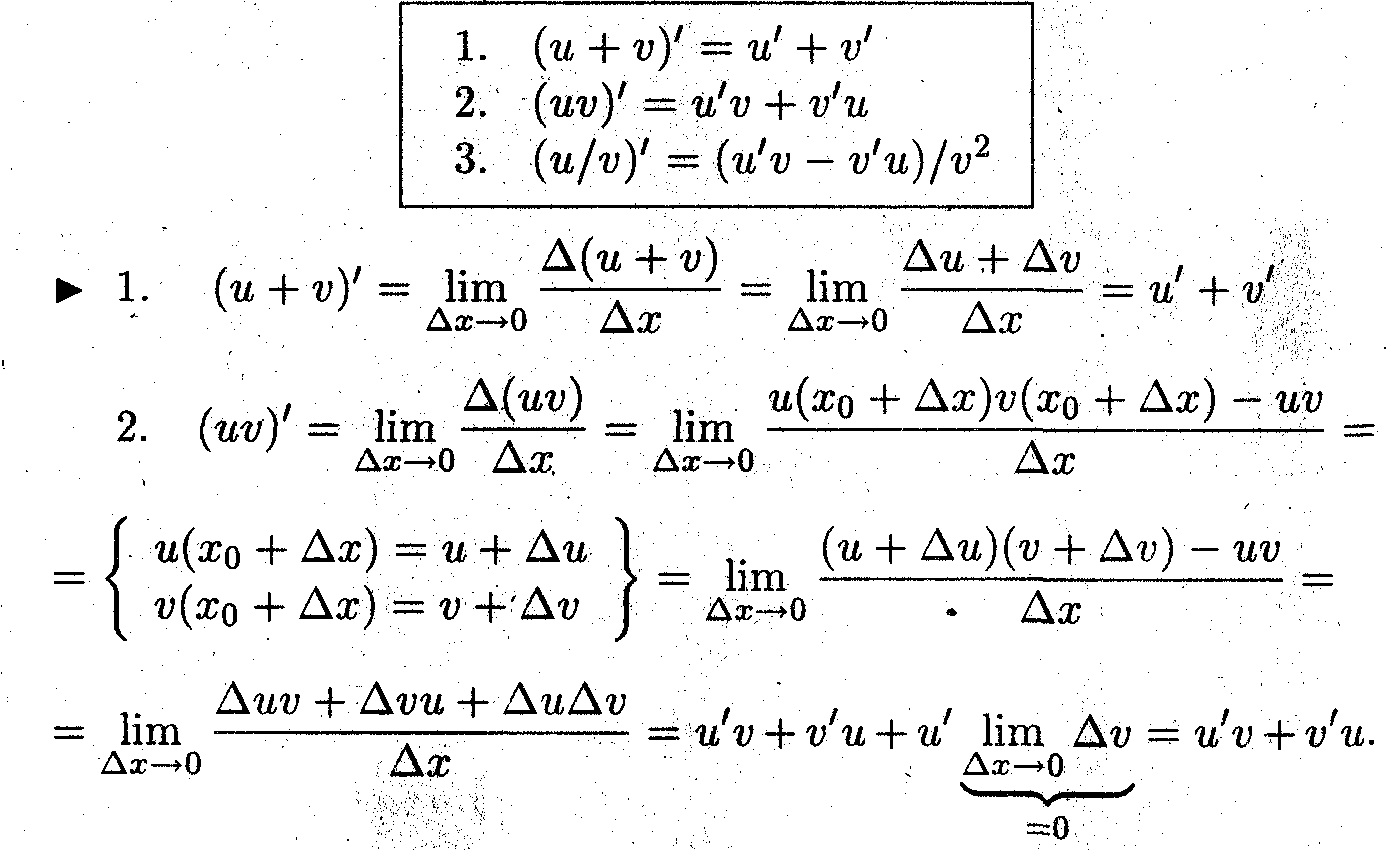
<Вернуться назад>