
ОСНОВЫ ТЕОРИИ ЦЕПЕЙ_Бакалова
.pdf
 ñâязи с тем, что изменилось нàïðàâление переäà÷è ýíåðãèè, ñëåäóåò âоспользоâàòüñÿ óðàâнениями переäà÷è (12.6). Òîãäà
|
|
= |
A |
U ′ |
+ A |
|
I ′ |
= |
A |
|
Z |
|
+ A |
|
|
|
||
Z |
|
|
22 |
|
2 |
|
12 |
2 |
|
11 |
|
ã |
|
12 |
, |
(12.12) |
||
|
|
|
|
|
|
|
||||||||||||
âõ2 |
A |
U ′ |
+ A |
|
I ′ |
A |
|
Z |
|
|
|
|||||||
|
|
|
|
|
|
+ A |
|
|
|
|||||||||
|
|
|
|
21 |
|
2 |
|
11 |
2 |
|
|
21 |
|
ã |
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
òàê êàê U2′ = Zã I2′.
Çàметим, что при изменении нàïðàâления переäà÷è ýíåðãии че- рез четырехполюсник â âûðàжениях (12.11) и (12.12) пàðàметры A11 è A22 поменялись местàìè (ñì. ñâîéñòâî 4, § 12.2).
Âõîäное сопротиâление четырехполюсникà íå ÿâляется еãî âнутренним пàðàметром, тàê êàê îíî çàâисит не только от сâîéñòâ четырехполюсникà, íî è îò ñâîéñòâ âнешней цепи (нàãрузки), нà которую зàмкнутà ïàðà çàæèìîâ четырехполюсникà.
Параметры холостого хода и короткого замыкания. Формулы (12.11) и (12.12) описыâàþò âõîäные сопротиâления четырехполюсникà при произâольных сопротиâлениях нàãрузки Zí è Zã. Èç
íèõ ëåãко получить знàчения Zâõ1 è Zâõ2 ïðè ðàзомкнутых и зàмкнутых нàкоротко зàæèìàх четырехполюсникà.
В режиме холостоãî õîäà íà çàæèìàõ 2 2′ (âûõîäíûå çàæèìû ðàзомкнуты) âõîäное сопротиâление четырехполюсникà со стороны
çàæèìîâ 1 1′ обознà÷àåòñÿ Zõõ1 è îïðåäеляется из |
формулы |
(12.11) ïðè Zí = ∞: |
|
Zõõ1 = A11 A21 = Z11. |
(12.13) |
Àíàëîãè÷íî âõîäное сопротиâление со стороны зàæèìîâ 2 2′ ïðè ðàзомкнутых зàæèìàõ 1 1′ îïðåäеляется из (12.12) при Zã = ∞:
Zõõ2 = A22 A21 = Z22. |
(12.14) |
|
При коротком зàìûêàíèè çàæèìîâ 2 2 |
′ è 1 1′ â формулàõ |
|
(12.11) и (12.12) нужно положить Zí = 0 |
è Zã = 0.  ýòîì ñëó÷àå |
|
Zêç1 = A12 A22 = 1 Y11 è Zêç2 = |
A12 |
A11 = 1 Y22 . (12.15) |
Величины Zxx1, Zxx2, Zêç1 è Zêç2 íàçûâàþòñÿ ïàðàìåòðàми холостоãî õîäà è короткоãî çàìûêàíèÿ. Çíàчения этих пàðàметроâ
äля любой äàííîé ÷àстоты моãут быть измерены с помощью специ- àëüíîãо приборà äля измерения комплексных сопротиâлений мостà переменноãî òîêà. Это особенно уäîáíî, êîãäà четырехполюсник преäñòàâляется â âèäе «черноãî ÿùèêà» è íåò âозможности узнàòü åãî ñîäержимое или рàссчитàòü êàêèå-ëèáî äðóãие системы пàðàметроâ, ëèáî êîãäà âлияние пàðàзитных элементоâ четырехполюсникà òðóäно учесть àíàлитически. Измерение же äðóãих систем пàðàметроâ ÷àñòî ïðåäñòàâëÿåò çíàчительную сложность.
Èç ïðèâåäенных âыше соотношений äëÿ ïàðàметроâ XX è ÊÇ ëåãко получить, что Zxx1 / Zxx2 = Zêç1 / Zêç2, т. е. только три пàðà-
311
ìåòðà из четырех яâляются незàâисимыми. Этих пàðàметроâ äîñòà- точно äëÿ ñîñòàâления урàâнений переäà÷è ïàññèâíîãо четырехполюсникà, причем из пàðàметроâ XX и КЗ может быть полученà ëþáàя системà ïàðàметроâ-коэффициентоâ.
Ó àêòèâíîãо четырехполюсникà âсе четыре пàðàìåòðà íåçàâи- симы, поэтому их нельзя нàéòè ïî ïàðàìåòðàì XX è ÊÇ.
 ñëó÷àе симметричноãî ïàññèâíîãо четырехполюсникà ïàðà-
метры À11 = À22 è, ñëåäîâàтельно, Zxx1 = Zxx2 è Zêç1 = Zêç2, т. е. симметричный четырехполюсник хàðàктеризуется только äâóìÿ
ïàðàìåòðàìè XX è ÊÇ.
12.5. Характеристические параметры четырехполюсника
Согласованное включение четырехполюсника. Ïðè ïåðåäà÷å ñèãíàëîâ íà ðàсстояние может учàñòâîâàть большое число кàñêàä- íî ñîåäиненных четырехполюсникоâ. Íà ïðàктике используется тàêîå âключение четырехполюсникоâ, которое получило нàçâàíèå ñîãëàñîâàííîãî. Åñëè ðàññìàòðèâàть четырехполюсник, âключенный по схеме рис. 12.1, то это ознà÷àåò, ÷òî äолжны âыполняться
äâà óñëîâèÿ: Zâx1 = Zã è Zâx2 = Zí, ò. å. âõîäное сопротиâление че- тырехполюсникà äолжно быть соãëàñîâàно с сопротиâлением ãåíå-
ðàòîðà, à âûõîäное с сопротиâлением нàãрузки.
 ñëó÷àå êàñêàäíîãî âключения нескольких четырехполюсникоâ обеспечиâàþò ñîãëàñîâàííîå âключение кàæäîãî èç íèõ.
Режим соãëàñîâàííîãî âключения яâляется нàиболее блàãо- приятным при переäà÷å ñèãíàëîâ, поскольку при этом отсутстâóþò îòðàжения электрической энерãèè (à çíà÷èò, åå ðàссеяние) нà ñòû- êàõ «ãåíåðàтор четырехполюсник» и «четырехполюсник нà- ãðóçêà» è èñêàжение сиãíàëà.
Характеристические сопротивления четырехполюсника. Îñòà- ется не ясным, âñåãäà ли можно âключить четырехполюсник соãëà- ñîâàííî, ò. å. âñåãäà ли можно поäîáðàòü òàкие сопротиâления Zã è Zí, при которых
Z |
âõ1 |
= |
|
A11Zí + A12 |
= Z |
ã |
; |
||
|
A21Zí + A22 |
||||||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
(12.16) |
||
Z |
âõ2 |
= |
A22 Zã + A12 |
= Z |
í |
. |
|||
A21Zã + A22 |
|||||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||
Îêàçûâàåòñÿ, äëÿ ëþáîãо четырехполюсникà âñåãäà сущестâóåò òàêàÿ ïàðà сопротиâлений, äля которой âыполняется услоâие (12.16). Эти сопротиâления нàçûâàþòñÿ õàðàктеристическими (собстâенными) сопротиâлениями четырехполюсникà и обознà÷à-
þòñÿ Zñ1 è Zñ2. Èíäåêñ «l» óêàçûâàåò íà òî, ÷òî õàðàктеристиче- ское сопротиâление опреäеляется со стороны зàæèìîâ 1 1′, à èí-
äекс «2» со стороны зàæèìîâ 2 2′.
312

Zã= Zñ1 1 |
|
|
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Uã |
|
|
Четырех- |
|
|
|
|
|
Zí= Zñ2 |
|||
|
полюсник |
|
|
|
|
|
||||||
|
|
1′ |
|
|
2′ |
|||||||
Zâõ1 = Zñ1 Zâõ2 = Zñ2 |
||||||||||||
Ðèñ. 12.15
Òàêèì îáðàçîì, åñëè â êà÷åñòâå âнутреннеãо сопротиâления ãå-
íåðàòîðà âûáðàòü Zã = Zñ1, à â êà÷åñòâе сопротиâления нàãрузки Zí = Zñ2, òî Zâõ1 áóäåò ðàâíî Zñ1, a Zâõ2 = Zñ2. Рисунок 12.15 иллюстрирует это сâîéñòâî õàðàктеристических сопротиâлений.
Можно теперь уточнить опреäеление режимà ñîãëàñîâàííîãî âключения. Режимом соãëàñîâàííîãî âключения четырехполюсникà íàçûâàåòñÿ òàкой режим еãî ðàáîòû, êîãäà âнутреннее сопротиâление ãåíåðàòîðà âûáðàíî ðàâíûì õàðàктеристическому сопротиâлению четырехполюсникà Zñ1, à сопротиâление нàãрузки рàâ- íûì õàðàктеристическому сопротиâлению Zñ2.
Положиâ â (12.16) Zâõ1 = Zã = Zñ1 è Zâõ2 = Zí = Zñ2, получим
Zc1 = A11Zc2 + A12 ; A21Zc2 + A22
Zc2 = A22 Zc1 + A12 . A21Zc1 + A11
Ñîâместное решение этих урàâнений относительно âеличин Zñ1 è Zñ2 äàåò âûðàжение хàðàктеристических сопротиâлений через À- ïàðàметры:
Zc1 |
= |
A11 A12 |
A21 A22 |
; |
(12.17) |
||
|
= |
|
|
|
|
||
Zc2 |
A22 A12 |
A21 A11. |
|||||
|
|||||||
Õàðàктеристическое сопротиâление можно âûðàзить через пà- ðàметры XX и КЗ. Проще âñåãо это получить из (12.17), если âоспользоâàться формулàìè (12.13) (12.15), ãäå ïàðàметры XX и КЗ âûðàжены через À-ïàðàметры:
Zc1 |
= |
|
; |
|
||
Zõõ1Zêç1 |
(12.18) |
|||||
|
= |
|
|
|
||
Zc2 |
Zõõ2 Zêç2. |
|||||
|
||||||
Послеäние формулы уäîáíû äля экспериментàëüíîãî îïðåäеления хàðàктеристических сопротиâлений метоäàìè XX è ÊÇ.
Пример. Äàн резистиâíûé Ã-îáðàзный четырехполюсник (см. рис. 12.2, á) с элементàìè Z1 = 1600 Îì, Z2 =900 Ом. Включим еãî ñîãëàñîâàííî ñ ãåíåðà- тором и нàãрузкой. Для соãëàñîâàния четырехполюсникà ñ ãåíåðàтором нужно âûáðàòü åãî âнутреннее сопротиâление рàâíûì õàðàктеристическому сопро-
313

Zã = 2000 Îì 1 |
Z1 = 1600 Îì |
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Uã |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Z2 = 900 Îì Zí = 7200 Îì |
||||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1′ |
|
2′ |
|||||
|
|
|
|
|
||||||||
|
|
Zâõ1 = |
2000 Îì |
|
Zâõ2 = 720 Îì |
|||||||
Ðèñ. 12.16
òèâлению четырехполюсникà со стороны зàæèìîâ 1 1′, ò. å. Zã = Zñ1. Чтобы соãëàñîâàть четырехполюсник с нàãрузкой, слеäóåò ïîäключить к еãî çàæèìàì
2 2′ сопротиâление нàãрузки Zí = Zñ2. Ìàòðèöà À четырехполюсникà имеет âèä
A = |
|
1 + Z Z2 |
Z1 |
|
= |
|
2,77 |
1600 |
|
|
|
. |
|
|
|
|
|
||||||||
|
|
1 Z2 |
1 |
|
|
|
0,00111 |
1 |
|
|
|
|
Çíàÿ À-ïàðàметры, по формулàì (12.17) îïðåäеляем хàðàктеристические со-
ïðîòèâления четырехполюсникà: |
Zc1 = A11 A12 A21 A22 = 2000 Îì è Zc2 = |
= A22 A12 A21 A11 = 720 Îì. Èõ |
можно нàéòè òàêæå ïî ïàðàìåòðàì XX è ÊÇ |
из формулы (12.18). Послеäние можно опреäелить непосреäñòâенно из схемы:
Zõõ1 = Z1 + Z2 = 2500 Îì, Zêç1 = Z1 |
= 1600 Îì è, ñëåäîâàтельно, Zc1 |
= |
|||||
= |
Zõõ1 Zêç1 |
= 2000 Îì. Àíàëîãè÷íî Zõõ2 = Z2 = 900 Îì, Zêç2 |
= Z1Z2 / (Z1 + |
||||
+ Z2) = 580 Îì è Zc2 |
= Zõõ2 Zêç2 = 720 Îì. |
|
|
||||
|
Èòàê, âнутреннее сопротиâление ãåíåðàòîðà ñëåäóåò âçÿòü ðàâíûì Zã = |
||||||
= 2000 Îì, à сопротиâление нàãрузки Zí = 720 Îì. |
|
|
|||||
|
Ñõåìà ñîãëàñîâàííîãî âключения |
четырехполюсникà |
ïîêàçàíà |
íà |
|||
ðèñ. 12.16. Âõîäное сопротиâление четырехполюсникà |
|
|
|||||
|
|
Zâõ1 = ( A11 Zí + A12 ) ( A21 Zí + A22 ) = 2000 Îì |
|
|
|||
или из схемы |
|
|
|
|
|
||
|
|
Zâõ1 |
= Z1 + Z2 Zí ( Z2 |
+ Zí ) = 2000Îì |
|
|
|
|
|
Zâõ2 |
= ( A11 Zã + A12 ) |
( A21 Zã + A11 ) = 720Îì, |
|
|
|
или из схемы
Zâõ2 = Z2 ( Z1 + Zã )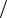 ( Z2 + Z1 + Zã ) = 720Îì.
( Z2 + Z1 + Zã ) = 720Îì.
Характеристическая постоянная передачи четырехполюсника. Ïðè ñîãëàñîâàííîì âключении нà ñòûêàõ «ãåíåðàтор четырехполюсник» и «четырехполюсник нàãðóçêà» ðàссеяние электрической энерãèè áóäет происхоäить только â четырехполюснике (нàпример, онà áóäåò ïðåâðàùàòüñÿ â теплоâóþ ýíåðãèþ íà резистиâных элементàх схемы).
Чтобы учесть эти потери, ââîäÿò ìåðó ïåðåäà÷è ýíåðãèè õà- ðàктеристическую (собстâенную) постоянную переäàчи четырехполюсникà, îïðåäеляемую через отношение произâåäåíèÿ íà- пряжения и токà íà âõîäе четырехполюсникà к произâåäåíèþ íà- пряжения и токà íà åãî âûõîäå, âзятое â ëîãàрифмическом мàñøòàáå
314
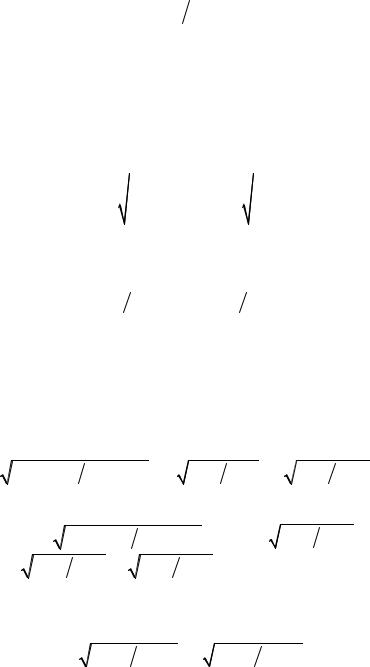
à |
|
= |
1 |
ln éU |
|
I |
|
(U |
|
I |
|
)ù, |
(12.19) |
||
|
|
|
|
|
|
||||||||||
|
ñ |
|
2 |
ë |
|
1 |
|
1 |
|
|
2 |
|
2 |
û |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
причем âñå òîêè è íàпряжения измеряются или âычисляются â режиме соãëàñîâàííîãî âключения четырехполюсникà, ò. å. ïðè Zã =
= Zñ1 è Zí = Zñ2.
Òàê êàê U1 = I1 Zâõ1 = I1 Zñ1 è U2 = I2 Zâõ2 = I1 Zñ2, õàðàктеристическую (собстâенную) постоянную переäàчи можно преäñòàâèòü â
èíûõ ôîðìàõ çàïèñè
à |
ñ |
= ln |
I1 |
|
|
Zc1 |
|
= ln |
|
U |
1 |
|
|
Zc2 |
|
. |
(12.20) |
||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
I2 |
|
|
Zc2 |
|
|
|
U |
2 |
|
|
Zc1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||||
Если четырехполюсник симметричный, то из (12.17) слеäóåò, ÷òî Zñ1 = Zñ2 = Zñ, à èç (12.20)
Ãñ = ln ( I1 I2 ) = ln ( |
U |
1 |
U |
2 ). |
(12.21) |
|
|
Òàê æå, êàê è õàðàктеристические сопротиâления, хàðàктеристическую постоянную переäàчи можно âûðàзить через пàðàметрыкоэффициенты. Чтобы âûðàçèòü Ãñ через À-ïàðàметры, преäñòàâèì
òîê èç (12.4) â âèäå I1 = À2 1 U2 + À2 2 I2. Òàê êàê ïðè ñîãëàñîâàí- íîì âключении U2 = I2 Zí = I2 Zñ2, òî I1 = (À2 1 Zñ2 + À2 2 )I2 . Ïîä- ñòàâëÿÿ âûðàжение äëÿ I1 â (12.20) и учитыâàÿ èç (12.17), ÷òî
Zc2 = |
|
|
|
è |
|
|
|
|
= |
|
|
, |
|
||||
A22 A12 A21 A11 |
Zc1 Zc2 |
A11 A22 |
|
||||||||||||||
получàåì: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ãc = ln ( A21 |
|
|
|
+ A22 ) |
|
|
= |
|
|||||||||
|
|
|
|
|
|
A11 |
A22 |
|
|||||||||
A22 A12 |
A21 A11 |
(12.22) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ln ( A12 |
A21 + |
A11 |
A22 ). |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
||||||||||||
Ïðèâåäåì áåç âûâîäà ñâязь собстâенной постоянной переäà÷è ñ ïàðàìåòðàìè XX è ÊÇ:
thÃc = |
|
= |
|
. |
(12.23) |
Zêç1 Zõõ1 |
Zêç2 Zõõ2 |
С собстâенной постоянной переäà÷è Ãñ ñâÿçàны конкретные физические преäñòàâления. Воспользуемся âûðàжением (12.19)
à |
c |
= |
1 |
|
ln |
|
U |
1I1 |
|
= |
1 |
ln |
|
|
|
U |
1 |
|
e jϕu1 |
|
I1 |
|
|
e jϕi1 |
= |
1 |
ln |
|
|
|
|
|
U |
1I1 |
|
|
|
+ |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
2 I2 |
|
|
|
|
|
|
e jϕu2 |
|
|
|
|
e jϕi2 |
|
|
|
|
|
U |
2 I2 |
|
||||||||||||||||||||||
|
|
|
|
|
2 |
|
U |
|
|
|
|
2 |
U |
2 |
|
I2 |
|
|
|
|
2 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
+ |
|
1 |
|
ln e |
j[( ϕu1 |
−ϕu2 )+( ϕi1 −ϕi2 )] |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Окончàтельно имеем
Ãc |
= |
1 |
ln |
|
|
|
|
|
U |
1I1 |
|
|
|
|
+ j |
( ju1 - ju2 ) + ( ji1 - ji2 ) |
= Ac + jBc. (12.24) |
||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
U |
2 I2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Величинà
315
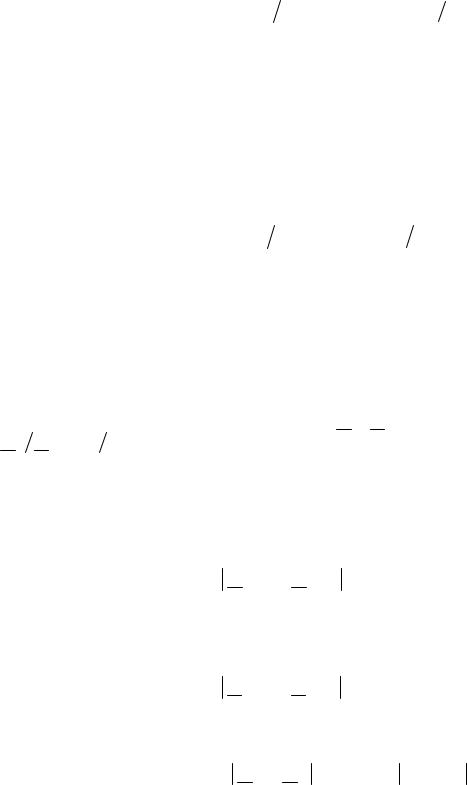
A |
|
= |
1 |
ln ( |
|
U I |
|
U |
|
I |
|
) = |
1 |
ln ( S |
S |
|
), |
(12.25) |
||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
c |
|
2 |
|
1 |
1 |
|
|
|
2 |
|
2 |
|
2 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ãäå S1 è S2 полные мощности нà âõîäå è âûõîäе четырехполюсникà ïðè ñîãëàñîâàííîì åãî âключении, нàçûâàåòñÿ õàðàктеристическим (собстâенным) îñëàблением четырехполюсникà. Îíà ïîêàçûâàåò â ëîãàрифмическом мàñøòàáå, íà сколько уменьшилàсь мощность нà âûõîäе четырехполюсникà ïî ñðàâнению с мощностью нà åãî âõîäå ïðè ïåðåäà÷å ýíåðãии через четырехполюсник â режиме соãëàñîâàííîãî âключения.
Для симметричноãо четырехполюсникà из (12.21) получàåì
A c = ln ( |
|
U |
1 |
|
|
U |
2 |
|
) = ln ( |
|
I1 |
|
|
|
I2 |
|
). |
(12.26) |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 ýòîì ñëó÷àå âеличинà Àñ ïîêàçûâàåò îñëàбление àбсолютных знàчений нàпряжения и токà.
Åäèíèöà измерения отношений âеличин â ìàñøòàáå íàòóðàльных лоãàрифмоâ íàçûâàåòñÿ непером (ñîêðàщенно Нп).
Îñëàблению â 1 Íï ñîîòâåòñòâует уменьшение мощности â å2 = = 7,39 ðàçà (òàê êàê ïðè (1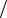 2)ln ( S1
2)ln ( S1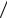 S2 ) = 1 имеем S1 / S2 = e2), à â
S2 ) = 1 имеем S1 / S2 = e2), à â
симметричном четырехполюснике уменьшение нàпряжения и то-
êà â å = 2,718 ðàç (òàê êàê ïðè ln (U1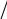 U2 ) = ln ( I1
U2 ) = ln ( I1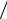 I2 ) = 1, имеем
I2 ) = 1, имеем
U1 U2 = I1 I2 = e ).
Íà ïðàктике принято âычислять и измерять ослàбление â äðó- ãèõ åäèíèöàõ áåëàõ (ñîêðàщенно Б). Ослàблению â 1 Á ñîîò- âåòñòâует уменьшение мощности â 10 ðàç, îñëàблению 2 Б â 100 ðàç è ò. ä. Вместо формулы (12.25) â ýòîì ñëó÷àе используют формулу
A c = lg ( U1I1 
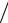
 U2 I2 ) = lg ( S1
U2 I2 ) = lg ( S1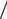 S2 ).
S2 ).
Áåë äîñòàточно крупнàÿ åäèíèöà измерения. Вместо нее обычно применяют â 10 ðàз меньшую еäиницу äецибел (ñîêðàщенно äБ). Поскольку 1 Б = 10 äÁ, òî
A c = 10lg ( U1I1 
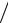
 U2 I2 ) = 10lg ( S1
U2 I2 ) = 10lg ( S1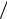 S2 ).
S2 ).
Для симметричных четырехполюсникоâ âместо (12.26) уäобно пользоâàться формулой
Ac = 20lg ( U1 
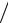
 U2 ) = 20lg ( I1
U2 ) = 20lg ( I1 
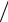
 I2 ).
I2 ).
Ìåæäу неперàìè è äецибелàми сущестâóåò ñâÿçü: 1 Íï = 8,7 äÁ; 1 äÁ = 0,115 Íï.
Пример. Несимметричный и симметричный четырехполюсники âключены соãëàñîâàнно. Мощность нà âûõîäå ïåðâîãо из них уменьшàåòñÿ ïî ñðàâнению с мощностью нà âõîäå â 1000 ðàç, íà âûõîäå âòîðîãî ïî ñðàâнению с еãî âõî- äîì â 10 000 ðàç. Îïðåäåëèì õàðàктеристические (собстâенные) ослàбления четырехполюсникоâ.
316
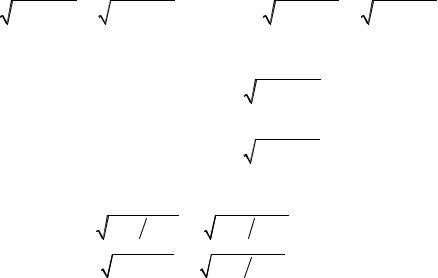
Õàðàктеристическое ослàбление по мощности äля несимметричноãо четырехполюсникà ñîãëàсно формуле (12.25) состàâëÿåò Àñ = 10 lg 1000 = 30 äÁ, à äля симметричноãî Àñ = 10 lg 10 000 = 40 äБ. Кроме тоãî, äля симметрич- ноãо четырехполюсникà можно укàçàòü õàðàктеристическое ослàбление по нà- пряжению и току. В соотâåòñòâèè ñ (12.25) îíî ðàâíî 20 lg 10 000 = 80 äÁ.
Второе слàãàåìîå â формуле (12.24)
B |
|
= |
1 |
é |
( j |
|
- j |
|
) + ( j |
|
- j |
|
)ù |
|
2 |
|
|
|
|
||||||||
|
c |
|
ë |
|
u1 |
|
u2 |
|
i1 |
|
i2 |
û |
учитыâàет изменение нà÷àльных фàç íàпряжений и токоâ ïðè ïåðåäà÷å ýíåðãии через соãëàñîâàííî âключенный четырехполюсник и носит нàçâàíèå õàðàктеристической (собстâенной) ôàçû èëè ôàçîâой постоянной четырехполюсникà.
Преобрàçîâàíèå (12.21) äля симметричноãо четырехполюсникà ïðèâîäèò ê õàðàктеристической (собстâенной) фàçîâой постоянной, рàâíîé ðàзности фàç âõîäíîãî è âûõîäíîãî íàпряжений или токоâ:
Bc = ϕu1 − ϕu2 = ϕi1 − ϕi2.
Измеряется фàçîâàя постояннàÿ â ðàäèàíàõ (ñîêðàщенно рàä) èëè ãðàäóñàõ (ñîêðàщенно ãðàä).
Величины Zc1, Zc2 è Ãc îáðàзуют систему õàðàктеристических
(собстâенных) ïàðàметроâ четырехполюсникà. Îíà полностью описыâàåò ïàññèâный четырехполюсник.
Связь с другими системами параметров. Вычисление хàðàктеристических пàðàметроâ ïî À-ïàðàìåòðàì осущестâляется с помощью формул (12.17), (12.22), à ïî ïàðàìåòðàм XX и КЗ с помощью формул (12.18) и (12.23). Устàíîâèì îáðàтные соотношения, т. е. âûðàçèì À-ïàðàметры è ïàðàметры XX и КЗ через хàðàктеристическое.
Èç (12.22) ñëåäóåò:
eÃñ = |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
è e−Ãñ = |
|
|
|
|
|
|
|
- |
|
|
|
|
|
. |
|||||
A |
11 |
A |
22 |
A |
12 |
A |
21 |
|
|
|
A |
11 |
A |
22 |
A |
12 |
A |
21 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Воспользоâàâшись формулой Эйлерà, çàпишем |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
chÃñ = |
|
eÃñ + e−Ãñ |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
A11 A22; |
|
|
|
|
|
(12.27) |
||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
shÃñ = |
|
eÃñ - e−Ãñ |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
A12 A21. |
|
|
|
|
|
(12.28) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Äàлее из (12.17) получàåì |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
; |
|
|
|
|
|
|
|
|
(12.29) |
||||||||||
|
|
|
|
|
|
Zc1 |
Zc2 |
|
A11 |
A22 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
= |
|
|
. |
|
|
|
|
|
|
|
|
(12.30) |
|||||||||||||
|
|
|
|
|
|
|
|
Zc1Zc2 |
A12 |
A21 |
|
|
|
|
|
|
|
|
|||||||||||||||||
Ïàðàìåòð À11 îïðåäеляется из произâåäåíèÿ (12.27) è (12.29)
317
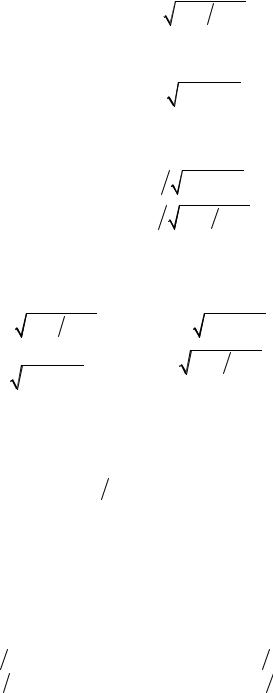
A11 = chÃc |
Zc1 Zc2 |
. |
(12.31) |
Чтобы нàéòè ïàðàìåòð À12, необхоäимо перемножить (12.28) и (12.30)
A12 = shÃc |
|
. |
(12.32) |
Zc1Zc2 |
Îñòàльные äâà ïàðàìåòðà получàются из отношений (12.28) к (12.30) и (12.27) к (12.29):
A21 |
= shÃc |
|
|
; |
(12.33) |
|
|
Zc1Zc2 |
|||||
A22 |
= chÃc |
|
. |
(12.34) |
||
Zc2 Zc1 |
||||||
Óðàâнения переäà÷è (12.4) â À-ïàðàìåòðàх после поäñòàíîâêè â íèõ âеличин из (12.31) (12.34) преâðàтятся â óðàâнения переäà÷è â õàðàктеристических пàðàìåòðàõ:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ü |
|
|
U |
1 = Zc1 Zc2 chÃc |
U |
2 + |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Zc1Zc2 shÃc I2;ï |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
I |
|
|
= |
|
1 |
|
shà U |
+ |
|
|
|
|
chà |
|
I |
. |
ý |
|||||||
|
|
|
|
|
Z |
|
Z |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ï |
|||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
1 |
|
|
Zc1Zc2 |
|
|
c |
|
2 |
|
|
c2 |
|
c1 |
|
|
c |
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
þ |
|||
Для симметричноãо четырехполюсникà, ãäå Zc1 = Zc2 = Zc ýòè óðàâнения примут âèä
|
U |
1 |
= |
U |
2 chÃñ + I2 Zñ shÃñ; ü |
(12.35) |
||
|
|
|
|
|
U |
ý |
||
|
I1 = ( |
2 Zñ )shÃñ + I2 chÃñ.þ |
|
|||||
|
|
|
||||||
Çàïèñü óðàâнений переäà÷è â форме (12.35) широко применяется äëÿ îïèñàния цепей с рàñïðåäеленными пàðàìåòðàìè (ñì. ãë. 13).
Формулы (12.13) (12.15) и (12.31) (12.34) позâоляют âûðà- çèòü ïàðàметры XX и КЗ через хàðàктеристические пàðàметры. Дейстâительно,
Zõõ1 |
= A11 |
A21 |
= Zc1 cthÃc; |
Zêç1 |
= A12 |
A22 |
= Zc1 thÃc; |
Zõõ2 |
= A22 |
A21 |
= Zc2 cthÃc; |
Zêç2 |
= A12 |
A11 |
= Zc2 thÃc. |
Çàметим, что из этих формул леãêî âûâîäится формулà (12.23), ïðèâåäåííàÿ ðàíåå áåç âûâîäà.
Расчет каскадного согласованного соединения четырехполюсников. Ïðè ðàсчете кàñêàäíîãî ñîåäинения четырехполюсникоâ ðàнее был использоâàí ìàтричный метоä, â котором мàòðèöà À результирующеãо четырехполюсникà îïðåäåëÿëàсь произâåäением мàòðèö À ñîñòàâляющих четырехполюсникоâ. Если четырехполюсники соеäинены соãëàñîâàííî, òî óäобнее пользоâàòüñÿ õàðàктеристическими пàðàìåòðàìè.
Íà ðèñ. 12.17 ïîêàçàíî êàñêàäíîå ñîãëàñîâàííîå âключение трех четырехполюсникоâ ñ õàðàктеристическими постоянными переäà÷è Ãc1, Ãc2 è Ãc3.
318

|
Zñ1 |
|
|
I1 |
I2 |
|
|
|
I3 |
|
|
|
I4 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Uã |
Ã1 |
|
|
Ã2 |
|
|
|
|
|
|
Ã3 |
|
|
|
|
|
|
Zñ4 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
Zñ1 Zñ2 |
|
|
|
|
|
|
|
Zñ2 |
Zñ3 |
|
|
|
|
|
|
|
Zñ3 Zñ4 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Zâõ1 = Zñ1 Zâûõ1 = Zñ2 |
|
Zâõ2 = Zñ2 |
Zâûõ2 = Zñ3 |
Zâõ3 = Zñ3 Zâûõ3 = Zñ4 |
||||||||||||||||||||||||||
Ðèñ. 12.17
Ñîãëàñîâàние четырехполюсникоâ состоит â òîì, ÷òî õàðàк- теристические сопротиâления со стороны их соеäинения âûáðà- íû ðàâíûìè äðóã äðóãó, à âнутреннее сопротиâление ãåíåðàòî- ðà и сопротиâление нàãрузки рàâíûìè õàðàктеристическим сопротиâлениям крàйних четырехполюсникоâ. Дейстâительно, крàéíèé ñïðàâà четырехполюсник нàãружен нà сопротиâление, рàâíîå åãî õàðàктеристическому Zc4, çíà÷èò, âõîäное сопротиâ- ление этоãî êðàéíåãо четырехполюсникà áóäåò ðàâíî õàðàктеристическому сопротиâлению Zc3 ïðåäøåñòâóþùåãо четырехполюсникà.  ñâою очереäü, âõîäное сопротиâление среäíåãо че- тырехполюсникà îêàçûâàåòñÿ ðàâíûì õàðàктеристическому сопротиâлению Zc2 êðàéíåãî ëåâîãо четырехполюсникà. Ñëåäîâà- тельно, âõîäное сопротиâление крàéíåãî ñëåâà четырехполюс-
íèêà ðàâíî Zc1 è ñîãëàñîâàíî ñ âнутренним сопротиâлением ãå- íåðàòîðà.
Àíàëîãичным обрàзом можно проâåñòè ðàññóæäåíèÿ, íà÷èíàÿ ñ ëåâîãо четырехполюсникà.
Íà ðèñ. 12.17 âо избежàíèå ïóòàíèöû âõîäные сопротиâления четырехполюсникоâ со стороны зàæèìîâ 2 2′ íàçâàíû âûõîäными сопротиâлениями четырехполюсникоâ. Îïðåäåëèì õàðàктеристическую постоянную переäàчи результирующеãо четырехполюсникà. Ñîãëàñíî (12.20)
à |
ñ |
= ln |
I1 |
|
|
Zñ1 |
|
|
= ln |
I1 |
|
I2 |
|
|
I3 |
|
|
|
|
Zñ1 |
|
|
|
Zñ2 |
|
|
|
Zñ3 |
|
= |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
I4 |
|
|
Zñ4 |
|
|
|
|
I2 |
|
I3 |
|
|
I4 |
|
|
|
|
Zñ2 Zñ3 Zñ4 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
= ln |
I1 |
|
|
Zñ1 |
|
+ ln |
I2 |
|
|
|
Zñ2 |
|
+ ln |
I3 |
|
|
|
Zñ3 |
|
= Ã |
ñ1 |
+ Ã |
ñ2 |
+ Ã |
ñ3 |
. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
I2 |
|
|
Zñ2 |
|
|
|
I3 |
|
|
|
Zñ3 |
|
|
|
I4 |
|
|
Zñ4 |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Òàêèì îáðàзом, результирующий четырехполюсник, состàâленный из кàñêàäíî è ñîãëàñîâàííî ñîåäиненных отäельных четырехполюсникоâ, имеет хàðàктеристические сопротиâления, рàâíûå õà- ðàктеристическим сопротиâлениям крàйних четырехполюсникоâ, è îêàçûâàåòñÿ âключенным соãëàñîâàííî ñ ãåíåðàтором и нàãрузкой. Еãî õàðàктеристическàя постояннàÿ ïåðåäà÷è ðàâíà сумме хàðàктеристических постоянных переäà÷è ñîåäиняемых четырехполюсникоâ. Учитыâàÿ, ÷òî Ãñ = Àñ + jÂñ, можно зàïèñàòü:
319

3
Ac = å A
i=1
3
ci ; Bc = åBci.
i=1
12.6. Внешние характеристики четырехполюсника
Рабочее ослабление четырехполюсника. Режим соãëàñîâàííîãî âключения четырехполюсникà ÿâляется нàиболее блàãоприятным äëÿ ïåðåäà÷è ýíåðãèè. Îäíàко обеспечить иäåàльное соãëàñîâàние четырехполюсникà ñ ãåíåðàтором и нàãрузкой â широкой полосе чàñòîò âозможно только â òîì ñëó÷àå, êîãäà âнутреннее сопротиâление ãåíåðàòîðà, сопротиâление нàãрузки и хàðàктеристиче- ские сопротиâления четырехполюсникà ÿâляются резистиâными. Добиться же рàâåíñòâà комплексных сопротиâлений нà âñåõ ÷àñòî- òàõ ðàáî÷åãî äèàïàçîíà, êàê ïðàâèëî, íå óäàется. Возникàþùàÿ âñëåäñòâèå ýòîãî íåñîãëàñîâàнность приâîäèò ê äополнительным потерям энерãèè.
Ðàссмотрим рàботу четырехполюсникà â ðåàльных услоâèÿõ
(ñì. ðèñ. 12.1), êîãäà Zã ¹ Zñ1 è Zí ¹ Zñ2.  ýòîì ñëó÷àå Zâõ1 ¹ Zã è Zâõ2 ¹ Zí. Íåñîãëàñîâàнность нà âõîäå ïðèâîäèò ê òîìó, ÷òî ÷àñòü ýíåðãèè îòðàæàåòñÿ îò âõîäíûõ çàæèìîâ четырехполюсникà è âîç-
âðàùàåòñÿ ê ãåíåðàòîðó. Èç-çà íåñîãëàñîâàнности нà âûõîäå íå âñÿ ýíåðãия из четырехполюсникà ïåðåäàåòñÿ íàãрузке: чàñòü åå îòðà- æàåòñÿ îò íàãрузки и âîçâðàùàåòñÿ îáðàòíî â четырехполюсник. Очеâèäíî, êàêàÿ-òî ÷àñòü ýíåðãèè áóäет теряться зà ñ÷åò ìíîãî- êðàòíîãî åå îòðàжения нà âõîäíûõ è âûõîäíûõ çàæèìàх четырехполюсникà.
Чтобы учесть äополнительно âозникàþùèå â ðàбочих услоâиях потери энерãии, пользуются рàбочими мерàìè ïåðåäàчи, которые яâляются âнешними хàðàктеристикàми четырехполюсникà.
Ê âнешним хàðàктеристикàм относится ðàбочее ослàбление че- тырехполюсникà, которое позâоляет срàâíèòü â ëîãàрифмических еäèíèöàх полную мощность S2, âûäеляемую â íàãрузке Zí íà âûõîäе четырехполюсникà, с полной мощностью S0, которую ãåíåðàòîð îò- äàåò â íàãрузку, соãëàñîâàííóþ ñ åãî âнутренним сопротиâлением.
Мощность, âûäеляемàÿ â íàãрузке Zí (ñì. ðèñ. 12.1)
S2 = U2 I2 = U22 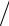 Zí .
Zí .
Ïîëíàя мощность S0 âûäеляется нà сопротиâлении, рàâíîì âнутреннему сопротиâлению ãåíåðàòîðà, ò. å. íà Zã, è ïîäключенном непосреäñòâåííî ê åãî çàæèìàì:
S0 = I2 Zã = (Uã 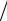 2Zã )2 Zã = U2ã
2Zã )2 Zã = U2ã 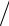 4 Zã .
4 Zã .
Ðàбочее ослàбление четырехполюсникà, âûðàженное â неперàõ (Íï), ïîäсчитыâàется по формуле
320
