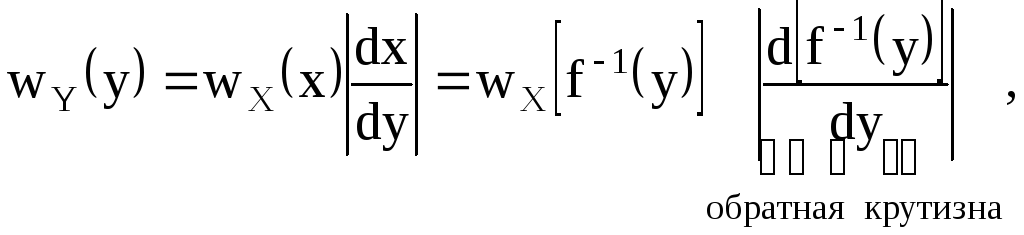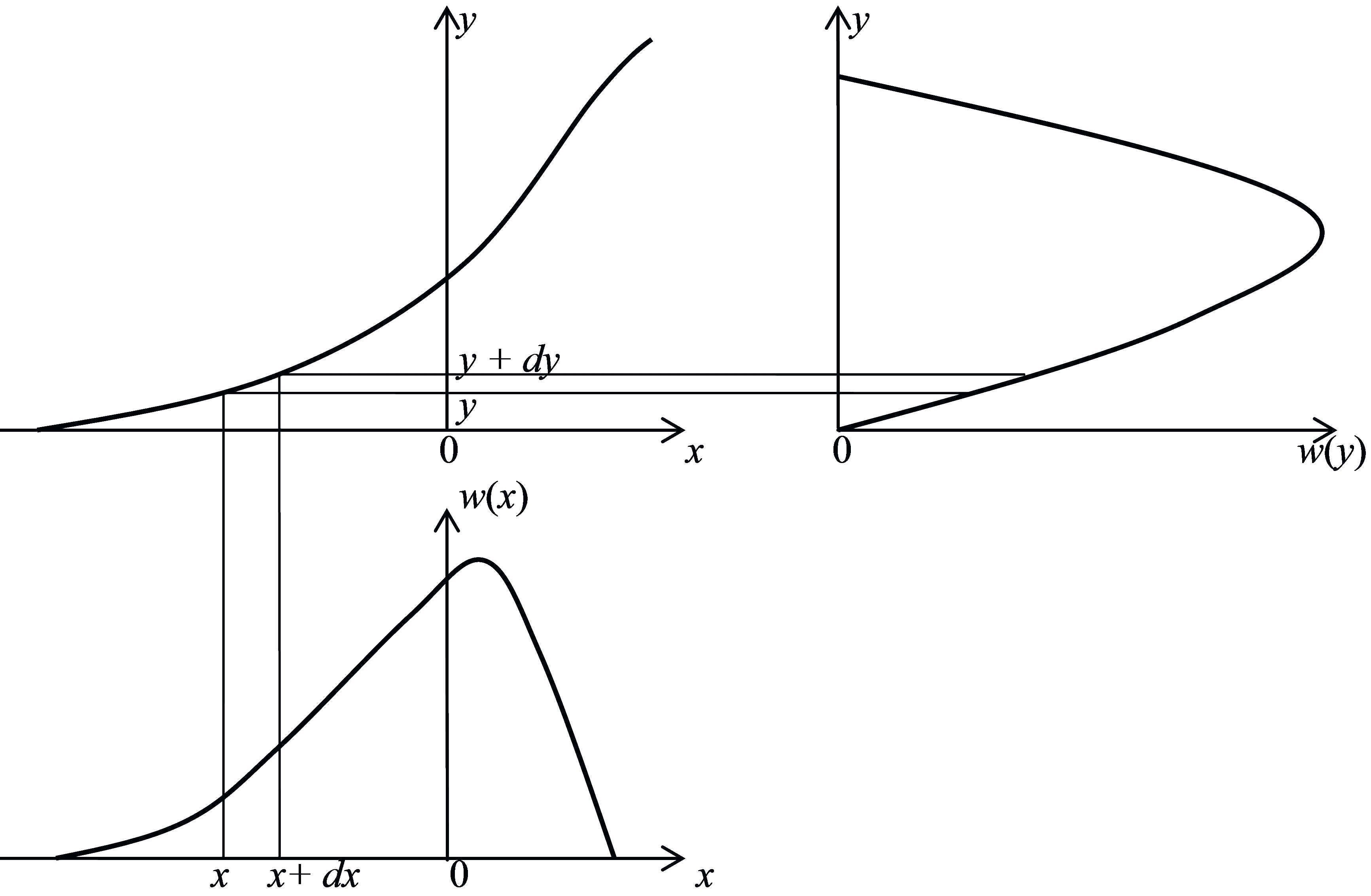Балтийский федеральный университет имени И. Канта

Физико-технический институт

Утверждаю

Заведующий кафедры

к.ф.-м.н., доцент

А. Шпилевой

«___»_________ 20__ г.

Л Е К Ц И Я № 13

Тема: «Прохождение случайных процессов через преобразователи сигналов»

Текст лекции по дисциплине: «Общая теория связи»

Обсуждена и одобрена на заседании кафедры

протокол №___ от «___»___________20__г.

Г. Калининград 2013 г. Текст лекции № 13

по дисциплине: «Общая теория связи»

«Прохождение случайных процессов через преобразователи сигналов»

Введение

В общем случае решение задачи прохождения заданного случайного процесса (СП) через конкретную электрическую цепь – функциональный узел (ФУ) произвольной сложности предполагает определение n – мерной плотности вероятности (или функции распределения) реакции цепи Y(t) на заданное случайное воздействие X(t) (рисунок 1.1).

Рисунок 1.1 – К постановке задачи прохождения случайного процесса через электрическую цепь

Однако общего метода решения такой задачи не существует. Поэтому ограничимся рассмотрением некоторых частных случаев.

1. Прохождение случайных процессов через безынерционные цепи

Безынерционная цепь (безынерционный функциональный узел (БФУ) полностью описывается функциональной зависимостью y = f(x), связывающей мгновенные значения воздействия x(t) и реакции y(t) в совпадающие моменты времени. В результате имеем дело с функциональным преобразованием случайного процесса Y(t) = f [X(t)].

Для вычисления одномерной плотности вероятности реакции w(y) по известной плотности вероятности воздействия w(x) рассмотрим рисунке 1.2, на котором изображены функциональная характеристика БФУ y = f (x), заданная плотность вероятности воздействия w(x) и искомая плотность вероятности реакции БФУ w(y). Учитывая, что при попадании случайной величины X в интервал (x, x+dx) случайная величина Y с вероятностью 1 попадает в соответствующий ему интервал (y, y+dy), можно написать следующее соотношение:

(1.1)

из которого вытекает:

				(1.2)
где		–	обратная функция (x = x(y) = f -1(y)).

Рисунок 1.2 – К расчету w(y) на выходе БФУ

Дифференциалы dx, dy и производная обратной функции в полученном выражении взяты по модулю в силу свойства положительности плотности вероятности.

Примеры:

1. Линейное безынерционное преобразование y = f (x) = ax + b.

(1.3)

Обратная функция определяется следующим выражением:

(1.4)

Таким образом, при линейном преобразовании случайной величины её кривая плотности распределения смещается на величину b, а масштаб по координатным осям изменяется в |a| раз.

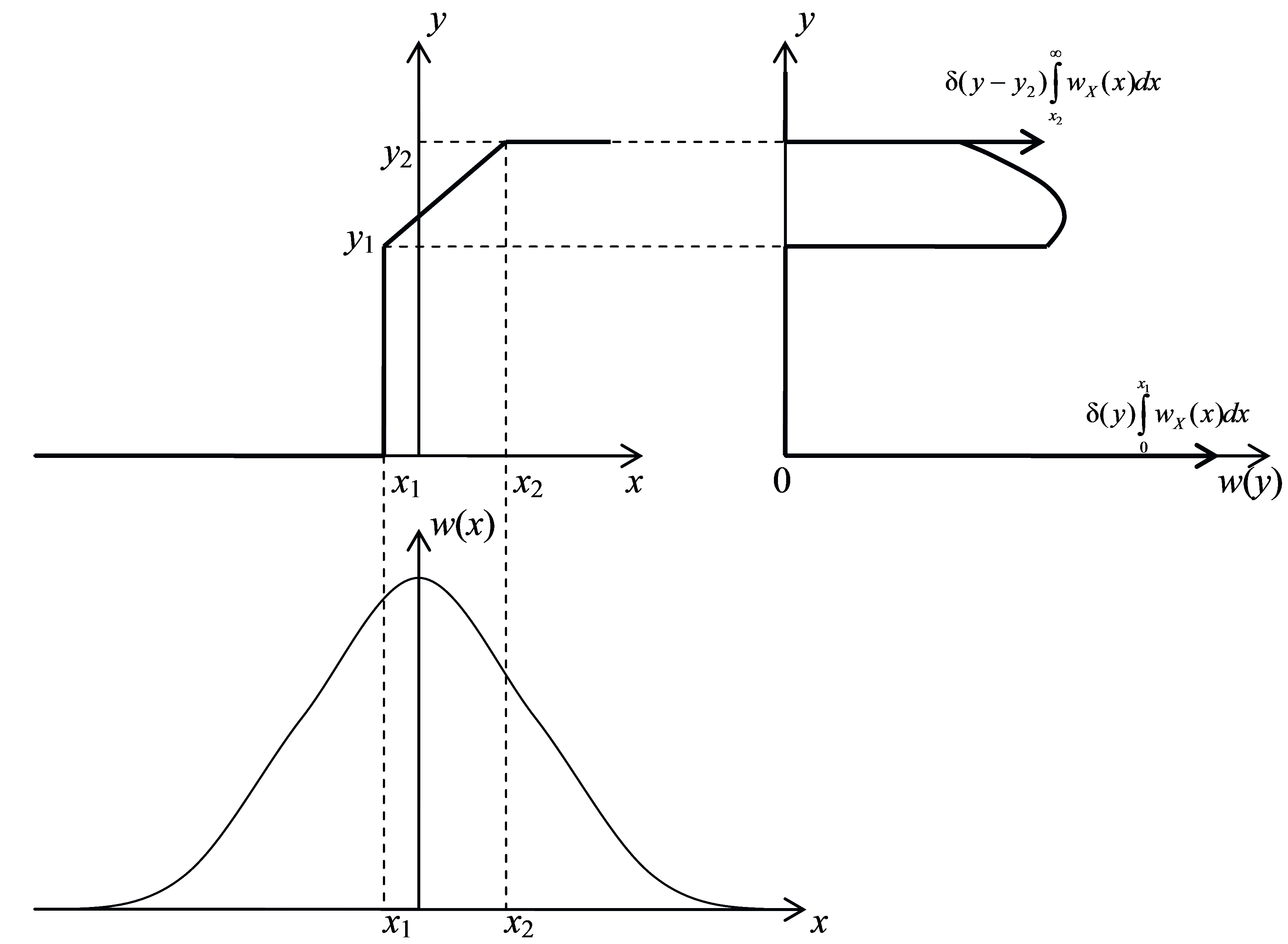
2. Кусочно-линейное преобразование y = f (x) (рисунок 1.3).

Задачу решим графически, определяя вид кривой w_Y (y) на отдельных интервалах оси у.

Рисунок 1.3 – Кусочно-линейное преобразование случайной величины

Из рассмотрения функциональной характеристики y = f (x) с очевидностью вытекает, что

а) при у < 0 и у > y₂ w_Y (y) = 0, т. к. значения реакции у не могут выйти за пределы уровней отсечки (у = 0) и насыщения (у = y₂);

б) при 0 < у < y₁ w_Y (y) = 0, т. к. в этот интервал (протяженностью y₁) значения реакции попадают при единственном значении воздействия x = x₁, вероятность которого w_X(x₁)dx  0:

			(1.5)
где

в) при y₁ ≤ у < y₂, где b = y₁, (см. пример 1):

(1.6)

г) при у = 0, т. к. у = 0 для всех х < x:

(1.7)

д) при у = у₂, т. к. у = у₂ для всех х > x₂.