решают систему уравнений второго закона Кирхгофа для контурных токов (систему контурных уравнений) и получают численные значения контурных токов в схеме;

через соотношения токов ветвей и контурных токов рассчитывают значения токов во всех ветвях схемы;

полученные значения токов ветвей подставляют в уравнения второго закона Кирхгофа для токов ветвей и проверяют правильность решения уравнений.

Поскольку число одновременно решаемых уравнений в методе контурных токов равно числу независимых контуров в схеме анализируемой цепи, то наиболее целесообразно использовать метод контурных токов для расчета цепей, в которых число контуров минимально, чтобы число уравнений метода контурных токов было также минимальным.

2.3.Анализ (расчет) сложных электрических цепей методом узловых потенциалов

Важным и часто используемым в электротехнике и радиоэлектронике методом расчета цепей является метод узловых потенциалов (МУП),

иногда называемый методом узловых напряжений.

Сущность метода узловых потенциалов заключается в следующем:

если были бы известны потенциалы узлов электрической схемы, то токи в ветвях схемы можно было бы легко найти по закону Ома для участка цепи.

Далее рассмотрим метод узловых потенциалов более подробно для той же, что и ранее, схемы сложной электрической цепи, приведенной на рис. 2.2. Для этого преобразуем исходную анализируемую схему рис. 2.2 к виду, показанному на рис. 2.7. Схема, приведенная на рис. 2.7, отличается

от исходной схемы рис. 2.2 тем, что в ней источники ЭДС E5 и E1 E1ЭКВ преобразованы в эквивалентные источники тока J5ЭКВ и J 1 соответствен-

но. Такое преобразование соответствует обратному показанному ранее пересчету источника тока (см. рис. 2.4, а) в источник ЭДС (см. рис. 2.4, б). В результате пересчета эквивалентные источники тока J5ЭКВ и J 1 оказыва-

ются равны:

24

Итак, пересчитав источники ЭДС E5 и E1 E1ЭКВ в эквивалентные им источники тока J5ЭКВ и J 1 , получим схему анализируемой цепи в ви-

де, показанном на рис. 2.7.

Приступим к составлению уравнений по методу узловых потенциалов. Для этого запишем токи всех ветвей схемы рис. 2.7 через потенциалы узлов схемы в предположении, что величины потенциалов узлов схемы известны:

После того как все токи ветвей схемы рис. 2.7 выражены через потенциалы узлов этой схемы, можно подставить эти токи в уравнения первого закона Кирхгофа (2.5):

25

Система уравнений (2.43) уже представляет собой систему уравнений, составленную по методу узловых потенциалов. Уравнения, входящие в систему (2.43), называют узловыми уравнениями. При этом следует учесть, что система уравнений первого закона Кирхгофа (2.5) содержит уравнения для узлов a, b, c анализируемой схемы рис. 2.7, а соответст-

вующее уравнение для узла d исключено из системы как линейно зависимое. В связи с этим и полученная система узловых уравнений (2.43) включает уравнения для узлов a, b, c и не содержит уравнения для узла d . Это

соответствует потенциалу d узла d, равному нулю (физически это означает, что узел d заземлен):

Заземленный узел (2.44) называют опорным.

J 1

J6

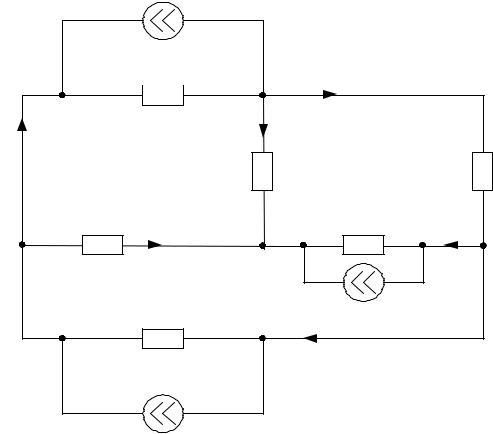
Рис. 2.7. Анализируемая схема сложной электрической цепи, преобразованная для метода узловых потенциалов

Заметим следующее: если заземлить узел d схемы рис. 2.7, то режим работы цепи не изменится, так как при заземлении одного из узлов линейной электрической схемы меняются только абсолютные значения потенциа-

26

лов, а их разности, определяющие падения напряжения и токи в схеме, остаются неизменными. С учетом (2.44) система уравнений (2.43) примет вид

Приведя подобные в левых частях уравнений системы (2.45) и перенеся в правые части этих уравнений токи источников тока, получим:

представляют собой суммы проводимостей всех ветвей, сходящихся в том узле, для которого составляется данное узловое уравнение (см. рис. 2.7).

Такие суммы проводимостей, сходящихся в одном узле, называют узловой проводимостью. Тогда узловые проводимости ga узла a , gb узла b и gc

узла c будут записаны так:

27

где проводимости отдельный ветвей схемы рис. 2.7 определены как величины, обратные их сопротивлениям:

Кроме узловых проводимостей в левой части уравнений системы (2.46) имеются так называемые межузловые проводимости. Межузловая проводимость – это проводимость, соединяющая два смежных узла. Например, между узлами a и b схемы рис. 2.7 включено сопротивление R1 ,

проводимость которого равна 1 ; поскольку эта проводимость в схеме

R1

включена между узлами a и b , её называют межузловой проводимостью и обозначают как gab или gba . Аналогично можно определить и обозначить и

другие межузловые проводимости. Для схемы рис. 2.7 запишем все межузловые проводимости:

Межузловые проводимости с участием узла d мы не рассматриваем, так как узловое уравнение для него в системе узловых уравнений (2.46) отсутствует (так как d 0 ).

После введения понятий узловой проводимости (2.47)–(2.50) и межузловой проводимости (2.51) система узловых уравнений (2.46) примет вид

Закономерность, наблюдаемая в структуре узловых уравнений полученной системы (2.52), может быть сформулирована как правило составле-

ния узловых уравнений: в левой части узлового уравнения для рассматриваемого узла записывают потенциал этого узла, умноженный на узловую проводимость, минус потенциал каждого из смежных узлов, умноженный на соответствующую межузловую проводимость, а в правой части уравнения записывают алгебраическую сумму токов, сходящихся в этом узле (втекающие в узел – с плюсом, вытекающие – с минусом).

Учтем, однако, что представленная выражением (2.52) система узловых уравнений очень удобна для формулировки правила составления узло-

28

вых уравнений. Для практического же использования систему узловых уравнений (2.46) и (2.52) следует переписать в ином виде. Если записать в правых частях уравнений этой системы те источники токов и ЭДС, которые имеют место в анализируемой схеме рис. 2.7, а в левых частях – сопротивления, установленные в этой схеме, то можно получить удобный для практических расчетов вид узловых уравнений:

Представленная в таком виде система узловых уравнений может быть непосредственно использована для проведения численных расчетов токов цепи, представленной на схеме рис. 2.7.

Приведем последовательность расчета (анализа) сложных электрических и радиоэлектронных схем методом узловых потенциалов:

заданную для анализа (расчета) электрическую схему перерисовывать с указанием на ней направлений искомых токов ветвей и обозначением узлов;

источники ЭДС пересчитать в эквивалентные источники тока;

записать систему уравнений по первому закону Кирхгофа для каждого узла;

записать соотношения для токов ветвей через разности потенциалов между узлами в схеме и учесть при этом источники тока (если они есть);

решить полученную систему уравнений и вычислить значения потенциалов узлов в схеме;

через соотношения токов ветвей и потенциалов узлов рассчитать значения токов во всех ветвях схемы;

полученные значения токов ветвей подставить в уравнения первого закона Кирхгофа для токов ветвей и проверить правильность решения уравнений.

Заметим, что, поскольку число одновременно решаемых уравнений в методе контурных токов равно числу независимых узлов цепи, то наиболее разумным представляется использование метода узловых потенциалов для электрических или радиотехнических схем так называемого параллельного типа, в которых число узлов минимально.

29