2.4. Применение нелинейных элементов в качестве параметрических

На практике в качестве параметрических элементов обычно применяют нелинейные элементы, работающие в определенных условиях. Предположим, что на нелинейный элемент одновременно действует несколько входных сигналов: . В общем случае полный отклик можно представить как:. В некоторых случаях отклик линейно зависит от одного из сигналов, например, - от:

(2.19)

где и- некоторые нелинейные функции.

Тогда нелинейная система оказывается линейной параметрической: линейной, так как , и параметрической, так как параметр системы, определяющий влияниена, зависит от времении не зависит от.

Пример. Пусть на нелинейный элемент (см. рис. 2.6) действует сумма гармонических колебаний:

(2.20)

причем

(2.21)

Условие (2.21) означает, что - небольшое отклонение от сильного сигнала. ВАХнелинейного элемента разложим в ряд Тейлора по степенями ограничимся в разложении линейным приближением:

(2.22)

где - крутизна характеристики, токопределяется лишь воздействием сильного сигнала, токзависит от воздействия обоих сигналовии определяется произведением меньшего из входных сигналов на дифференциальный параметр элемента – крутизну, управляемый сильным сигналом. Так какпериодически изменяется с частотой, то и крутизнаизменяется периодически с частотой:

(2.23)

Зависимость (2.23) свойственна линейным () параметрическим (параметрзависит от времени) цепям.

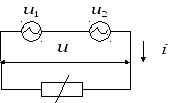
Рис.2.6

Вывод: Если на нелинейный элемент действуют одновременно слабый и сильный сигналы, то по отношению к слабому сигналу нелинейный элемент ведет себя как линейный параметрический элемент, управляемый сильным сигналом.

Сказанное относится не только к резистивным элементам, но и к реактивным элементам.

Пример. Пусть на нелинейную емкость с вольткулонной характеристикой действует напряжение (2.20). Аналогично (2.22) получаем

(2.24)

Отклик (2.24) на нелинейной емкости приближенно определяется суммой двух сигналов. Первый из них – отклик на действие только сильного сигнала, а второй – отклик на действие более слабого сигнала, равный произведению слабого сигнала на дифференциальную емкость , периодически изменяющуюся под действием сильного сигнала. То есть, по отношению к слабому сигналу нелинейная емкость приближенно ведет себя как линейная параметрическая, изменяющаяся с частотой.