7. Нелинейные избирательные системы под внешним воздействием

7.1. Нелинейные системы под внешним воздействием

В нелинейной системе, находящейся под внешним воздействием, возникают вынужденные процессы. В частности, в системе с высокодобротной колебательной системой – вынужденные колебания. Частотные характеристики колебательного контура с нелинейной индуктивностью или емкостью отличаются от таковых для линейного контура:

1) резонансная частота зависит от амплитуды колебаний;

2) при плавном изменении частоты воздействия возможны скачкообразные изменения амплитуды вынужденных колебаний;

2) АЧХ и ФЧХ нелинейного контура по форме несимметричны;

3) при внешнем воздействии на автоколебательные системы возникают такие явления, как синхронизация колебаний, деление частоты, асинхронное возбуждение и гашение колебаний;

4) частота вынужденных колебаний может существенно отличаться от частоты внешнего воздействия даже не обязательно в целое число раз;

5) при незначительном изменении режима работы нелинейного устройства или воздействия (амплитуды или частоты входного сигнала) может резко измениться характер вынужденных колебаний;

Нелинейные неавтономные системы часто исследуют квазилинейным методом или методом медленно меняющихся амплитуд. Метод фазовой плоскости в обычном виде применяется редко, так как наличие членов с явной зависимостью от времени в уравнениях неавтономных систем приводит к явной зависимости от времени уравнений фазовых траекторий (), что резко усложняет анализ. Однако для изучения неавтономных автоколебательных и параметрических систем на фазовой плоскости применяютимпульсно-фазовый метод. Тогда входной сигнал заменяется эквивалентными короткими импульсами.

Общая методика изучения системы с высокодобротным нелинейным колебательным контуром на основе квазилинейного метода или метода медленно меняющихся амплитуд следующая. Если на систему действует периодическое колебание , то напряжение на контуре

(7.1)

где огибающая и начальная фазамедленно меняются по сравнению с частотой вынужденных колебаний.

Частота находится из физических соображений: при изучении явления синхронизации полагают, а делении частоты враз -. Предположение о значенииможет оказаться верным в ограниченной области изменения параметров системы или вообще неверным. Пусть найдено выражение (7.1) для стационарных колебаний (прии). Могут они действительно реализоваться или нет, выясняется при проверке их устойчивости.

Вывод. Применение квазилинейного метода или метода медленно меняющихся амплитуд к исследованию неавтономной системы позволяет определить амплитуду и фазу (а не частоту) колебаний.

7.2. Резонанс в нелинейной системе

На рис. 7.1 показан параллельный колебательный контур с нелинейной емкостью. Через контур протекает гармонический ток частоты- внешнее воздействие. Из-за высокой добротности (избирательности) контура установившееся напряжение на нем будет практически гармоническим на той же частоте:

(7.2)

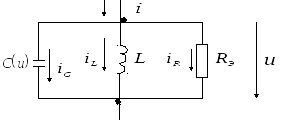
Рис. 7.1

Ток в емкостной ветви контура

(7.3)

где - дифференциальная емкость,.

Аппроксимируем зависимость относительно смещения в рабочей точке:

(7.4)

где коэффициенты ,и- положительные.

Подставим (7.2) и (7.4) в (7.3) и выделим первую гармонику тока:

Тот же ток можно получить, если вместо нелинейной включить эквивалентную линейную емкость

(7.5)

называемую также средней емкостью по первой гармонике.

Резонансная частота контура

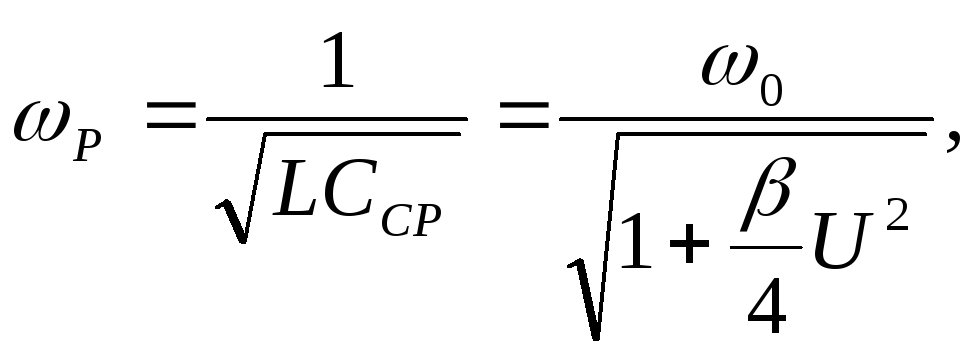(7.6)

где , зависит от амплитудыколебаний напряжения.

Если , то разлагая (7.6) в ряд Тейлора и ограничиваясь двумя первыми членами разложения, имеем:

(7.7)

то есть увеличение амплитуды вызывает уменьшение резонансной частоты по параболическому закону.

Рис. 7.2

На рис. 7.2 пунктирной линией показана частотную характеристику линейного контура с емкостью при заданном значении амплитуды тока через контур. Сплошная линия показывает частотную характеристику нелинейного контура. Каждой точке первой характеристики соответствует точка последней характеристики с тем же значением ординаты, но со смещением по оси абсциссна величину. Частотная характеристика нелинейного контура оказывается несимметричной. Для заштрихованной области характеристика нелинейного контура оказывается неоднозначной. При плавном изменении частотыэто приводит к гистерезисным явлениям и скачкам амплитуды. Снимем частотную характеристику при заданной амплитуде тока через контур, увеличивая частоту. Сначала напряжениеизменяется плавно вдоль кривой. Призначениевозрастает скачком на величину. При дальнейшем увеличении частоты значенияплавно уменьшаются вдоль кривой. Если теперь уменьшать частоту, то сначала амплитудаплавно изменяется вдоль кривой. Призначениепадает скачком на величину. После этого амплитудаизменяется плавно по ветви. Заштрихованная область на рис. 7.2 соответствует гистерезисной области, где значения амплитудызависят от способа установления частоты. Участок ветвиэкспериментально не может быть получен, так как соответствующие ему стационарные режимы оказываются неустойчивыми.

Чем меньше амплитуда тока через контур, тем меньше выражена асимметрия его характеристики. При достаточно малых значениях амплитуды этого тока заштрихованная область неоднозначности характеристики контура исчезает. Тогда гистерезиса и скачков амплитуды при периодическом изменении частоты тока через контур уже не наблюдается.

Кратко остановимся на поведении неавтономного контура с нелинейной индуктивностью (см. рис. 7.3).

Рис. 7.3

Учитывая поведение дифференциальной индуктивности, можно получить, что с увеличением амплитуды напряженияна колебательном контуре значение средней индуктивности по первой гармоникебудет уменьшаться, а резонансная частота- увеличиваться. Зависимостьсоответствует пунктирной линии на рис. 7.4, частотные характеристики наклонены в сторону более высоких частот.

Рис. 7.4