4.6.2.Перемножители, инвентор и сумматор

Добавил:

tinkapunka Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный университет телекоммуникаций им. проф. М.А. Бонч-Бруевича

Предмет:

Теория электрической связи

Файл:

метода по курсачу.pdf

Скачиваний:

Добавлен:

24.05.2023

Размер:

2.36 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 128 9 10 11 12 > Следующая >>>

Но если эти импульсы на рис. 26, г, д, е, ж, з подать на вход согласованного фильтра (СФ) с импульсом g3(t) x1н (t 3T ) (рис. 26, г), то соот-

ветствующие импульсы на выходе СФ будут импульсами Найквиста, обеспечивающими отсутствие межсимвольной помехи при взятии отсчетов главных максимумов этих импульсов.

СФ находится в приемном устройстве (ПрУ) и входит в состав демодулятора.

Подробно это будет изложено в разделе о работе демодулятора для квадратурной модуляции.

В итоге в сигнал на выходе сумматора КАМ или КФМ входят случайные процессы Iф (t) и Qф (t) , ансамбли которых соответствуют полученной

ранее формуле (46):


Iф (t) In g3	t nT ;	Qф (t) Qn g3	t nT ,	(66)
n		n

где In (t) и Qn (t) – независимые случайные величины, принимающие из-

вестные дискретные значения с заданными вероятностями, какие они имеют в формулах (35) и (40);

g3(t) x1н (t 3T ) – детерминированный импульс, спектральная плотность которого выражается через спектральную плотность импульса Найквиста.

со скоростью

. Переносчиками информационных символов

4.6.2.1.Корреляционные функции и спектральные плотности мощности случайных сигналов на выходе CФФ

В разд. 4.4 по формуле (28) определена корреляционная функция стационарного случайного процесса X (t) , в котором в качестве переносчиков

информационных символов Xn используются детерминированные импульсы g(t nT ) . Формула (28) имеет вид

BX (τ) X n2 T1 Bg (τ) ,

где X n2 – математическое ожидание квадрата случайной величины X n ;

T1 – частота поступления в канал связи информационных символов Xn;

Bg ( ) – автокорреляционная функция детерминированного импульса g(t) , определяемая равенством (29),

Bg ( ) g(t) g(t )dt .

Стационарный случайный процесс Iф (t) на выходе СФФ1 передает по каналу связи информационные символы In , поступающие в канал

являются импульсы g3(t nT ) . Поэтому формула (28) для корреляционной функции BIф ( ) стационарного процесса Iф (t) принимает вид

( )

I 2

( ).

(67)

Iф

Определим математическое ожидание

In2

для КАМ-16. Информаци-

онные символы In принимают значения 3h, h,

h , 3h с одинаковой ве-

роятностью P(3h) P(h) P( h ) P ( 3h) 0, 25 .

Математическое ожидание In2

будет равно

I 2 = P(3h) (3h)2

P(h) h2 P( h ) ( h)2 P ( 3h) ( 3h)2

0,25 9h2 h2 h 2 9h2 5h2.

Для КФМ-4 аналогично получим

I 2

h2 .

Таким образом, имеем

, для КАМ-16;

In2

(68)

для КФМ-4.

Определим автокорреляционную функцию Bg

( ) , входящую в (67).

В равенстве (29) при замене g(t) g3(t) получим

(τ)

g3 (t) g3 (t τ)dt ,

(69)

где согласно (65) и (63) имеют место равенства

g (t) x

(t 3T ) ; x

(t)

x (t) ,

1н

1,27

аx1(t) определяется (62).

Врезультате (69) будет иметь вид

Полученный интеграл является автокорреляционной функцией Bx1( ) импульса x1(t) . Поэтому равенство, определяющее Bg3 ( ) , представим

в форме

Bg3 ( ) T 2 Bx1( ) . 1,27

Если в равенстве (50) обозначение аргумента t изменить на , то равенство (50) представим в виде

Bx1( ) = x( ) .

С учетом этого равенства функцию Bg3 ( ) можно представить следующим образом

			Bg	( )				T					x( ) .		(70)

											2
				3		1,27					2
						1,27
	Подставляя (70) в (67), окончательно определим корреляционную
функцию BIф ( ) случайного процесса Iф (t) на выходе СФФ:

			BIф		( )				In	2				x( ) ,	(71)
			BIф		( )		1, 27					2		x( ) ,	(71)
							1, 27

где In		2 – определяется (68);
	x( ) – импульс Найквиста при значении 1.
	Учитывая график функции x( )									на рис. 19, а, представим график
функции BIф ( ) , изображенный на рис. 27.

In2

BIФ ( ) BQФ ( )

1,272

4T	3T	2T	T	T	2T	3T	4T
	Рис. 27. График корреляционных функций BI				( ) и	BQ ( )
					ф	ф
		случайных процессов Iф (t) и Qф (t)
							на .
	Напомним, что в равенстве (50) сделано изменение обозначения аргумента t						на .

В соответствии с теоремой Винера – Хинчина определим спектраль-

ную плотность мощности GIф ( )

случайного процесса Iф (t)

GIф

( ) BIф ( )e i d

Используя (71), будем иметь

In2

x( ) e i d

1, 27

Так как полученный интеграл определяет спектральную плотность Sx ( )

импульса Найквиста x(t) при значении 1, то согласно (43) получим

In2

1 cos

;

( ) 1, 27

(72)

График спектральных плотностей мощности GIф ( ) , соответствую-

щий (72), показан на рис. 28.

GI ( ) GQ ( )

I 2 T

1,272

Рис. 28. График спектральных плотностей

мощности

( ) и GQ

( )

Так как случайный процесс Qф (t) на выходе нижнего сглаживающего

формирующего фильтра (СФФ) имеет такие же вероятностные характеристики, как и процесс Iф (t) , то можно написать следующие равенства:

BQф	( ) BIф	( )		In	2		x(t),
			1, 27			2

				5h2		T			T		2
				5h2		T			T		2
							1	cos		,			;
					2	2	1	cos		,	T		;
GI		( ) GQ	1, 27			2			2		T			.	(73)
GI	ф	( ) GQ	( )											.	(73)
	ф	ф										2
												2
			0,											.
			0,											.
												T
												T

В заключение раздела отметим, что корреляционные функции (72) и спектральные плотности мощности (73) случайных процессов Iф (t) и

Qф (t) на выходе СФФ определены без учета усеченности импульсов x1(t) и x(t) . Ранее отмечалось, что возникающая погрешность при таком подходе будет незначительной с практической точки зрения.

4.6.2.2. Сигналы квадратурной модуляции КАМ-16 и КФМ-4

На структурной схеме системы связи (рис. 1) сигнал Qф (t) sin ct

c выхода нижнего СФФ и далее с выхода нижнего перемножителя поступает на вход инвертора, который изменяет знак перед этим сигналом с плюса на минус. С учетом этого на выходе сумматора получаем сигнал s(t)

s(t) Iф (t) cos ct Qф (t)sin ct .

(74)

Этот сигнал в зависимости от заданного вида модуляции является сигналом квадратурной амплитудной или квадратурной фазовой модуляции. Множители cos ct и sin ct обеспечивают ортогональность сигналов

Iф (t) cos ct и Qф (t)sin ct . Поэтому говорят, что эти сигналы находятся

в квадратуре.

Сигналы, входящие в (74), передаются одновременно, в одной и той же полосе частот, по одной линии связи.

Свойство ортогональности обеспечивает линейную независимость этих сигналов, а значит, и возможность их разделения на приемном конце канала. Возможность резделения этих сигналов позволяет независимо производить оценку информационных параметров (модулирующих символов) In и Qn в составе сигналов Iф (t) и Qф (t) . Используя полученные ранее вы-

ражения (35) из разд. 4.5 для сигналов Iф (t) и Qф (t) , формулу (74) запишем в виде


s(t) In g3	t nTs cos ct Qn g3	t nTs sin ct.	(75)
n	n

Выделим из правой части (75) сигнал sk (t) , которому соответствует

слагаемое с индексом n k , где k – произвольное фиксированное целое число:

sk (t) Ik g3 t kTs cos ct Qk g3 t kTs sin ct (76)g3 t kTs Ik cos ct Qk sin ct .

С помощью сигнала (76) по каналу передаются информационные (модулирующие) символы Ik и Qk . Сигнал (76) появляется на выходе модулятора, начиная с момента t kTs , и его длительность равна длительности усеченного импульса g3(t kTs ), т. е. равна 6Ts .

Из разд. 4.5 следует, что символы Ik и Qk явля-

ются декартовыми координатами точки M на сиг-

нальном созвездии (рис. 29), которая соответствует

выделенным слагаемым из выражения (75).

Согласно

рис. 29

параметры Ik и Qk

можно

представить в виде

Ik Uk cos k ,

Qk Uk sin k ,

(77)

Рис. 29. I

и Q

–

координаты точки M

на сигнальном созвездии

где U

I 2 Q2 и

arctgQ

в декартовой системе

Величины Uk и k – координаты той же точки

координат

M на сигнальном созвездии

в полярной системе

координат. Подставив (77) в (76), преобразуем сигнал sk (t) к виду

sk (t) g3 t kTs Uk cos k cos ct Uk sin k sin ct

(78)

g3 (t kTs ) Uk cos ct k .

Из (78) видно, что в состав выделенного сигнала в качестве сомножи-

теля входит гармоническое колебание

Uk cos ct k ,

(79)

представленное в канонической форме. Представление гармонического колебания (79) в канонической форме

в составе сигнала (78) получено благодаря знаку «минус» в выражении (74) перед вторым слагаемым. Этот знак обеспечивается введением инвертора в нижнюю ветвь перед сумматором на структурной схеме (рис. 1).

Гармоническому колебанию (79) соответствует комплексная амплитуда

U	k	U	k	e j k ,	(80)
	k		k

Как следует из учебников и учебных пособий по теории электрических цепей и теории сигналов [5–9], при записи гармонического колебания в канонической форме перед начальной фазой k должен стоять знак плюс, как в выражении (79). При этом

численное значение начальной фазы k в каждом конкретном случае может быть величиной положительной или отрицательной.

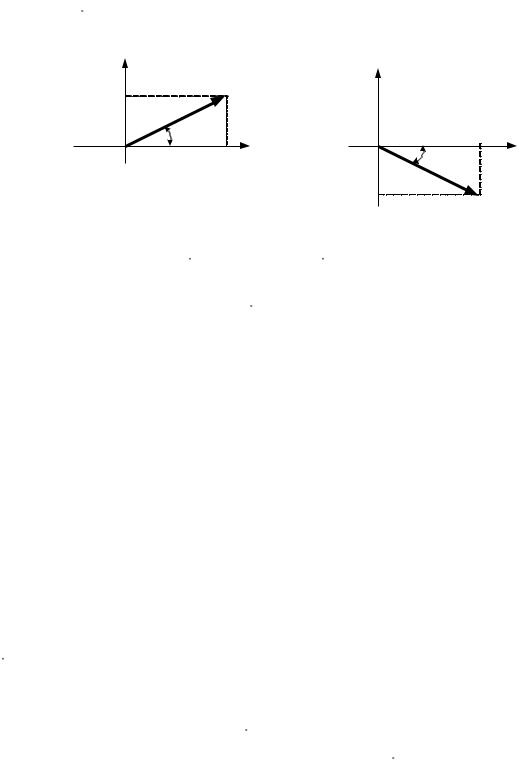
которая при условии, что k 0 , представлена на комплексной плоскости вектором Uk (рис. 30, а).

а)

i k

б)

i k

U Ue

Рис. 30. Вектор комплексной амплитуды:

а) U

e j k ; б) U

e j k

Существенно, что вектор Uk

по длине и направлению полностью со-

ответствует исходному вектору с координатами Ik и

Qk точки М на сиг-

нальном созвездии на рис. 29.

Поскольку в (78) гармонический сигнал представлен в канонической форме, а выражение (78) было получено из сигнала (74), то выражение (74) является канонической формой для сигнала квадратурной модуляции (КАМ, КФМ).

Если в структурной схеме исключить инвертор перед сумматором, то-

гда сигнал на выходе сумматора будет представлен в виде
sКАМ (t) Iф (t) cos ct Qф (t)sin ct.	(81)

В этом случае, повторив приведенные выше выкладки, в составе выделенного сигнала получим гармонический сигнал в форме Uk cos( ct k ) ,

которая не является канонической, как упоминалось ранее. Вектор комплексной амплитуды для данного гармонического сигнала будет иметь вид

Uk Uk e j k . На комплексной плоскости этот вектор при условии k 0

изображен на рис. 30, б.

Сравнивая рис. 30, б и 29, делаем вывод, что при задании сигнала sКАМ (t) в форме (81) вектор Uk на комплексной плоскости не совпадает по направлению с соответствующим вектором Uk на сигнальном созвез-

дии на рис. 29. Это является следствием того, что форма (81) не является канонической для представления сигнала КАМ, и от этого возникает отмеченное несоответствие.

Таким образом, из двух возможных представлений сигнала квадратурной модуляции в форме (74) или в форме (81), будем считать канонической только форму (74) и только ее будем использовать в КР.

При определении корреляционной функции случайного сигнала на выходе модулятора необходимо уточнить задание ансамблей случайных процессов на выходах перемножителей.

При задании ансамблей этих процессов предполагается, что имеется ансамбль одинаковых передающих устройств, по которым передаются различные реализации случайных процессов Iф (t) и Qф (t) .

В состав каждого передающего устройства (ПерУ) входит свой генератор гармонического колебания cos( ct ) , где начальная фаза при-

нимает какое-то детерминированное численное значение. Множество этих различных значений образует случайную величину c, т. е. каждое является реализацией случайной величины c.

При задании случайных процессов на выходе перемножителей, де-

терминированные функции cos ct	и sin ct , входящие в (74), необходимо
расширить до случайных функций	cos ct с	и sin( ct с ) введением
в аргумент детерминированных функций cos ct		и sin ct случайной фазы

c, не зависящей от случайных процессов Iф (t) и Qф (t) . Тогда вместо (74) получим случайный процесс s(t) следующего вида:

s(t) Iф (t) cos( ct с ) Qф (t) sin( ct с ) .

(82)

Случайный процесс s(t) в (82) позволяет правильно определить кор-

реляционную функцию случайного сигнала КАМ или КФМ на выходе

сумматора.

Обращаем внимание на случайную фазу c. В каждой отдельной реализации случайного процесса, определенного по формуле (82), фаза c имеет свое численное значение, которое не изменяется во времени. Случайный же характер фазы c проявляется в том, что для разных реализаций значения c отличаются друг от друга и ансамбль этих значений образует случайную величину c с равномерной плотностью вероятности w( с ) на интервале 0 2 ,

	1		при 0 с 2 ;
		,
	2	,					(83)
w( с )	2						(83)
0,			при	с	0,		2 .
				с		с

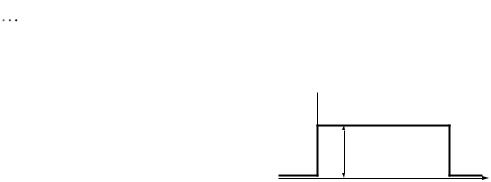
График w( с ) изображен на рис. 31. Только при равномерной плотности веро-

ятности w( с ) для случайной фазы c (рис. 31)

случайный процесс на выходе модулятора (на выходе сумматора) будет стационарным.

w( C )

1/ 2

Рис. 31. Равномерная плотность вероятности w( с )

4.6.2.3. Корреляционные функции и спектральные плотности мощности случайных cигналов на выходах перемножителей

На выходе верхнего перемножителя (ПМ-1) получаем сигнал

Iф (t) cos( ct с ) .

Определим математическое ожидание этого случайного сигнала
Iф (t) cos( ct с ) Iф (t) cos( ct с ) .	(84)

Это равенство получено на основании того, что сомножители Iф (t) и cos( ct с ) представляют собой независимые случайные процессы. Ранее отмечалась о независимость случайной фазы с от сигнала Iф (t) . Случайный процесс Iф (t) , полученный по выражению (46):


Iф (t)	In g3	t nT ,
	n

формируется на выходе блока СФФ при подаче на его вход случайного

процесса I (t) In g2 (t nT ) с выхода блока ФМС. Причем блок СФФ

трансформирует прямоугольные импульсы g2 (t nT ) в импульсы g3(t nT ) .

Значения информационных символов (ИС) In

при этом не изменяются.

Определим математические ожидания

Iф (t) и cos( ct с ),

входя-

щие в (84):

Iф (t)

= In g3 (t nT ) =

g3 (t nT ) ,

(85)

где g3(t nTS ) – детерминированный сигнал.

Согласно (37) из разд. 4.5 можем написать для КАМ-16

In ( 3h) p( 3h) ( h) p( h) h p(h) 3h p(3h)

( 3h) 0,25 ( h) 0, 25 h 0, 25 3h 0, 25 0.

Аналогично для КФМ-4 получим

In 0 .

(86)

Подставляя (86) в (85), получим

Iф (t) 0 .

(87)

Следовательно, Iф (t) – центрированный процесс.

Математическое ожидание сигнала cos( ct с ), зависящего от слу-

чайной величины с

с равномерной плотностью вероятности

w( с ) (83)

на интервале 0

2 , определим по формуле

cos( t )w( )d

2 cos( t )d

0 . (88)

cos( t )=

Подставляя (87) и (88) в (84), получим

Iф (t) cos( ct с ) 0 .

(89)

Это равенство означает, что случайный процесс Iф (t)cos( ct с ) является центрированным, поэтому корреляционная функция BIфcos (t1,t2 )

этого процесса определяется по формуле

BIфcos (t1,t2 ) = Iф (t1) cos( ct1 с ) Iф (t2 )cos( ct2 с ) =


= Iф (t1) Iф (t2 ) cos( ct1 с ) cos( ct2 с ) .					(90)

Равенство (90) получено на основании известного положения теории вероятностей о том, что математическое ожидание от произведения независимых случайных сомножителей равно произведению математических ожиданий этих сомножителей.

Математическое ожидание Iф (t1) Iф (t2 ) в (90) равно корреляционной функции BIф (t1,t2 ) центрированного случайного процесса Iф (t) (87), т. е.

BIф (t1,t2 ) = Iф (t1) Iф (t2 ) .

Необходимо отметить, что процесс Iф (t) , помимо свойства центриро-

ванности, обладает также свойством стационарности, так как процесс стационарный получается в результате прохождения центрированного стацио-

нарного процесса I (t) через СФФ, который является линейным фильтром. С учетом свойства стационарности процесса Iф (t) можем написать

BIф (t1,t2 ) = BIф (t2 t1) .

Как известно из курса ОТС, при подаче на вход любого линейного фильтра центрированного, стационарного процесса выходной процесс будет также центрированным и стационарным.

Рассмотрим математическое ожидание другого сомножителя в (90):


					cos( ct1 с ) cos( ct2										с ) =
	1		cos (t				t		)	1		cos (t			t			) 2					=	(90а)
			cos (t			2	t		)			cos (t			t		2	) 2				с	=	(90а)
	2				c	2		1		2			с	1			2					с
	2									2

	1	cos (t					t		)	1		cos[ (t			t			) 2 ] =						(90б)
		cos (t				2	t		)			cos[ (t			t	2		) 2 ] =						(90б)
	2				c	2		1		2			с	1		2					с
	2									2
			1
=			1	cos (t				t )				1	cos[ (t t							) 2 ] .				(90в)
=				cos (t			2	t )					cos[ (t t						2	) 2 ] .				(90в)
			2		с		2		1		2			с	1				2				с
			2								2

В этой цепочке преобразований первое равенство (90а) получено в ре-

зультате использования формулы cos соs = 12 cos( ) + cos( ) .

Второе равенство (90б) получено на основании известного положения теории вероятностей – математическое ожидание суммы случайных слагаемых всегда равно сумме математических ожиданий слагаемых.

Третье равенство (90в) получено на основании правила: математиче-

ское ожидание детерминированной величины 12 cos с (t2 t1) равно самой


детерминированной величине. Второе слагаемое	1	cos (t	t		) 2
детерминированной величине. Второе слагаемое		cos (t	t	2	) 2	с
	2	с 1		2		с
	2

в сумме равенства (90в) является математическим ожиданием случайной величины 12 cos с (t1 t2 ) 2 с , так как в аргумент косинуса входит слу-

чайная фаза 2 с . Аналогично (88) получим: cos с (t1 t2 ) 2 с = 0. Итак, равенство (90) принимает следующий вид:

(t ,t

) B

t , t

cos

) cos (t

t ) . (91)

Iфcos

Iф

Вводя обозначение (t2

t1) , равенство (91) представим в виде

( )

( ) cos .

(92)

Iф cos

I ф

Таким образом, на выходе перемножителя получаем случайный процесс Iф (t)cos( сt с ) (66). Математическое ожидание этого процесса со-

гласно (89) равно нулю, т. е. постоянно, и его корреляционная функция BIфcos (t1,t2 ) , учитывая (91), зависит от разности времен (t2 t1) . Следо-

вательно, случайный процесс на выходе перемножителя является стационарным.

Корреляционная функция BIф ( ) случайного процесса Iф (t) опреде-

ляется формулой (71). Подставляя (71) в (92), окончательно получаем

BIф cos ( )	1		In2		x( ) cos с .	(93)
	2	1, 27		2

На рис. 32 представлен график функции BIф cos ( ) , где x( )						– импульс
Найквиста (при коэффициенте ската 1).

		B	(τ)	1	B		( ) cosω τ
		IФcos	2			IФ	c
		IФcos				IФ
1	I 2
	n
2 1,272

				τ
2T			0	2TS
2T	S	TS		2TS
	S			TS
				TS

Рис. 32. Корреляционная функция BIф cos ( )

случайного процесса Iф (t) cos( сt с )

Спектральную плотность мощности случайного сигнала на выходе перемножителя определим на основании теоремы Винера – Хинчина. Преобразуя функцию BIф cos ( ) по Фурье, с учетом (93) получим

													1						1
GIф cos ( ) BIф cos ( ) e i d													1	In2					1					x( ) cos с e i d ,
GIф cos ( ) BIф cos ( ) e i d													2	In2				1,27			2			x( ) cos с e i d ,
													2					1,27
учитывая, что cos						ei с e i с							, имеем
учитывая, что cos													, имеем
				с				2
								2
1			1					i( )					1										1			i( )
1		2	1	x( ) e				i( )					1					2					1		x( ) e	i( )
		In								с		d					In									с	d
	4	In	1,272							с		d			4		In			1,272						с	d
					1				In2	S	x	( ) S										x		( ) ,			(94)
										S		( ) S												( ) ,			(94)
				4			1, 272									с									с
				4			1, 272

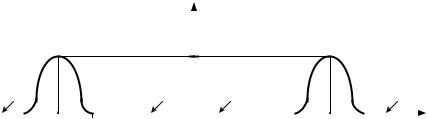
где графики функций Sx ( с ) и Sx ( с ) получаются в результате сдвига графика функции Sx ( ) (43) на рис. 19, б соответственно вправо и влево на величину с .

Напомним, что функция Sx ( ) импульса Найквиста x(t) при значении

коэффициента ската 1 и

равна

cos

при

;

Sx ( )

при

Нетрудно показать, что имеет место равенство.

sin ( ) BI

cos ( ) .

(95)

Отсюда получаем

cos ( ) GQ

sin ( ).

(96)

GI cos( ) GQ

sin( )

1,272

Рис. 33. Спектральные плотности мощности

cos ( ) и

GQ sin ( )

случайных процессов Iф (t) cos( сt с )

и Qф (t) cos( сt с )

на выходе перемножителей

4.6.2.4. Корреляционная функция и спектральная плотность мощности случайного процесса s(t) на выходе модулятора (сумматора)

Согласно структурной схеме системы связи (рис. 1) на выходе модулятора (сумматора) получаем сигнал s(t) квадратурной модуляции КАМ-16 или КФМ-4, ссылаясь на выражение (82) в разд. 4.6.2.2:

s(t) = Iф (t) cos( сt с ) Qф (t) sin( сt с ) .

В соответствии с изложенным в разд. 4.6.2.2 математическое ожидание s(t) 0 , тогда можно утверждать, что s(t) является центрированным случайным процессом, поэтому его корреляционная функция будет следующей:

Bs (t1,t2 ) s(t1) s(t2 )

Iф (t1) cos сt1 с Qф (t1)sin сt1 с

cos сt2 с Qф (t2 )sin сt2 с

Iф (t2 )

Имея в виду известные свойства математического ожидания, можно

написать

Iф (t1) cos сt1 с Iф (t2 )cos сt2 с

cos сt1 с Qф (t2 )sin сt2

Iф (t1)

Qф (t1) sin сt1 с Iф (t2 )cos сt2

sin сt1 с Qф (t2 )sin сt2

Qф (t1)

Iф (t1) Qф (t2 ) cos сt1 с cos( сt2 с ) Iф (t1) Qф (t2 )

cos( сt1 с ) sin( сt2 с ) Qф (t1) Iф (t2 ) sin( сt1 с ) cos( сt2 с )

Qф (t1) Qф (t2 ) sin( сt1 с ) sin( сt2 с ) .

После преобразований получим

cos t

sin (t

t )

Iф

Iф , Qф

sin( t

cos

t .

Qф

Здесь Iф (t) и Qф (t)

являются независимыми случайными процессами,

поэтому взаимные корреляционные функции равны нулю:

t2 t1 B

t2 t1 0.

Iф , Qф

Qф , Iф

Тогда получим

B (t ,t

)

t ) cos (t

t )

t ) cos (t

t ).

s 1

Cогласно (73)

имеем

(t2 t1) = BI

(t2

t1)

. В результате получим

Bs (t1,t2 ) Bs (t2 t1) BI ф (t2

t1)cos с (t2 t1) . Вводя обозначение

(t2 t1) ,

будем иметь

Bs ( ) BIф ( ) cos c .

(97)

Используя (71), окончательно получим

		1
B ( ) I 2		1	x( ) cos ,	(98)

		1,272
s	n	1,272	c

где x( ) – импульс Найквиста, определяемый (42) при 1 (рис. 19, б);

In2 – определяется формулой (68) для КАМ-16 или для КФМ-4. График функции Bs ( ) приведен на рис. 34.

In2 Bs(τ) BIФ( ) cosωcτ

1,272

2TS	TS	0	TS	2TS

Рис. 34. График корреляционной функции Bs ( )

Спектральная плотность мощности Gs(ω) случайного сигнала s(t) в соответствии с теоремой Винера – Хинчина определяется через преобразование Фурье корреляционной функции Bs(τ). Используя (98), получим

									1
Gs ( )	BIф cos ( ) e i d In2								1		x( ) cos c e i d
Gs ( )	BIф cos ( ) e i d In2							1,27		2	x( ) cos c e i d
								1,27

		1		In2	S	x	( ) S				x	( ) ,		(99)
					S		( ) S					( ) ,		(99)
	2		1, 272						c				c
	2		1, 272

где согласно (59) получим аналитические выражения для функции Sx ( c )

и Sx ( c )

	T	1 cos			T		при
		1 cos					при
	2		c	2
	2			2
Sx c
						при
0						при

c 2 c 2 , при c 2 ;

T T T

c 2T ;

	при c	2		c			2		;

			T				T

при				2		2		.

	c			T	c	T

<<< < Предыдущая 1 2 3 4 5 6 78 / 128 9 10 11 12 > Следующая >>>

Соседние файлы в предмете Теория электрической связи

#
29.12.202219.53 Кб13Kalendarny_plan_KR.docx
#
29.12.20229.51 Кб43KURSOVIKani.m
#
29.12.20221.72 Mб168курсач ТОР final.docx
#
24.05.20232.36 Mб21метода по курсачу.pdf