
- •Основные обозначения.
- •1. Элементарные сведения.
- •Контрольные задания
- •2. Комплексные числа.
- •555 Решение алгебраических уравнений.
- •3. Линейная алгебра. Матрицы и основные операции с ними.
- •Определители 2-го и 3-го порядка.
- •Решение систем линейных уравнений с помощью определителей.
- •Контрольные задания
- •4. Аналитическая геометрия. Системы координат на плоскости и в пространстве.
- •Векторы и линейные операции над ними.
- •Скалярное, векторное и смешанное произведения векторов.
- •555 Прямая на плоскости и различные способы её задания.
- •555 Прямая и плоскость в пространстве и различные способы их задания.
- •555 Линии второго порядка.
- •555 Некоторые поверхности второго порядка.
- •Контрольные задания
- •5. Функции одного аргумента. Понятие функции и способы задания.
- •Предел функции и числовой последовательности.
- •Понятие числового и степенного ряда.
- •Непрерывность функции, точки разрыва.
- •Контрольные задания
- •6. Производная и дифференциал.
- •555 Приближенное решение уравнений.
- •Контрольные задания
- •7. Неопределенный интеграл.
- •Свойства неопределённых интегралов.
- •Контрольные задания
- •8. Определенный интеграл.
- •Приложения определённого интеграла:
- •9. Функции нескольких аргументов.
- •10. Дифференциальные уравнения.
- •Методы решения основных типов дифференциальных уравнений первого порядка.
- •11. Общая задача линейного программирования.
- •Контрольные задания
- •Приложение. Задачи для подготовки к экзамену.
- •Учебная литература.
10. Дифференциальные уравнения.
Дифференциальным уравнением называется равенство, содержащее независимые переменные, неизвестные функции и их производные. Если независимая переменная одна, то уравнение называется обыкновенным дифференциальным уравнением, а иначе дифференциальным уравнением в частных производных. Порядком дифференциального уравнения называется наивысший порядок встречающихся в нём производных. Обыкновенным дифференциальным уравнением 1-го порядка, разрешённым относительно производной называется уравнение вида y¢=f(x,y), где y - неизвестная функция, а f - заданная функция двух аргументов.
Методы решения основных типов дифференциальных уравнений первого порядка.
Уравнение вида y¢=f(x)g(y) называется уравнением с разделяющимися переменными. Оно решается так: умножим обе части на dx, разделим на g(y) и проинтегрируем. При этом если g(y0)=0, то y=y0 тоже является решением.
Уравнение вида
![]() называется
однородным уравнением. Замена неизвестной
по формуле y=zx
приводит
к уравнению с разделяющимися переменными.
называется
однородным уравнением. Замена неизвестной
по формуле y=zx
приводит
к уравнению с разделяющимися переменными.
Уравнение вида y¢+f(x)y=g(x) называется линейным уравнением. Для его решения делаем замену y=uv. Получим u¢v+uv¢+f(x)uv=g(x); u¢v+u(v¢+f(x)v)=g(x); v¢+f(x)v=0; найдём какое-нибудь v и подставим в предыдущее равенство: u¢v=g(x); найдя отсюда u и подставив в y получим ответ.
Уравнение вида y
= xy¢+f(y¢)
называется
уравнением
Клеро.
Общее решение уравнения Клеро имеет
вид
y = xC+f(C).
Особое
решение уравнения Клеро имеет вид:
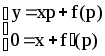 ,
где p
- параметр.
,
где p
- параметр.
Пример 1.
Решить уравнение y = xy¢+y¢3
Общее решение
уравнения имеет вид
y = xC+C3
.
Особое
решение уравнения имеет вид:
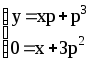 .
Исключая p
получим
27y2
+ 4x3=0.
.
Исключая p
получим
27y2
+ 4x3=0.
Ответ: y = xC+C3 ; 27y2 + 4x3=0.
666
Решить уравнения:
1. y¢ = x3y5 2. y¢ = eylnx
3.
y¢
=
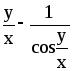 4.
y¢
=
4.
y¢
=
![]()
5.
y¢sinx
- y = sinxsin(x/2) 6. xy¢
- y = x![]()
7. y = xy¢+siny¢ 8. y = xy¢+lny¢
555
Линейные дифференциальные уравнения с постоянными коэффициентами.
Уравнение ay²+by¢+cy=0 называется линейным однородным уравнением второго порядка с постоянными коэффициентами. Для его решения составим уравнение al2 + bl + c = 0. Пусть его корни l1 и l2. Тогда возможны три случая:
1)
l1
и l2
действительны и различны Þ
![]()
2) l1 = l2 =l Þ y=C1elx+C2elx
3) l1 и l2 комплексные l1,2 = a±ib Þ y=eax(C1cos(bx) +C2sin(bx))
666
9. y² + 2y¢ - 3y = 07. y² + 2y¢ - 3y = 0
10. y² - 2y¢ - 8y = 0
11. y² + 2y¢ + y = 0
12. y² - 4y¢ + 4y = 0
13. y² + 2y¢ + 2y = 0
14. y² - 2y¢ + 5y = 0
15. y²¢ - 3y² + 3y¢ - y = 0
16. y² + 2y¢ - 3y = x - 3x2
17. y² - 2y¢ - 8y = 6e4x
18. y² - y = (4+3x)e2x
19. y(4) - 4y² + 3y = 0
555
Приближенное решение задачи Коши для обыкновенного дифференциального уравнения 1-го порядка.
Пусть дано уравнение y¢=f(x,y) с начальным условием y(x0) = y0.
Простейший способ приближённого решения - метод Эйлера. Для этого задаётся шаг h и значения y вычисляются по формулам:
xn = xn-1 + h
yn = yn-1 + hf(xn-1,yn-1)
Погрешность этого метода имеет порядок h.
Уточнённый метод Эйлера:
x* = xn-1 + h/2
y* = yn-1 + 0,5hf(xn-1,yn-1)
xn = xn-1 + h
yn = yn-1 + hf(x*,y*)
Погрешность этого метода имеет порядок h2.
666
Решить приближённо с шагом h=0,1 на отрезке [0;1] уточнённым методом Эйлера
18. y¢ = y3 + x3, y(0) = 1 19. y¢ = y2 - xy + x2, y(0) = -1
20.
y¢
= (y/x)3
+ (x/y)3,
y(0) = 1 21. y¢
=
![]() ,
y(0) = 1
,
y(0) = 1
555
Ответы
1. y-4+x4=C 2. e-y = x(1 - lnx) + C 3. sin(y/x)+ln|x| + C
4.
y = xeCx 5.
y = (2sin(x/2) + C)tg(x/2) 6. y = 2x![]() + Cx
+ Cx
9. y = C1e-3x + C2ex 10. y = C1e-2x + C2e4x 11. y = C1e-x + C2 xe-x
12. y = C1e2x + C2 xe2x 13. y = C1e-x sinx + C2e-x cosx
14. y = C1e2x cos2x + C2ex sin2x 15. y = C1ex + C2 xex + C3 x2ex
16. y = C1e-3x + C2ex +x2 - x 17. y = C1e-2x + C2e4x + xe4x
18. y = C1ex + C2e-x + xe2x 19. y = C1ex + C2e-x + C3eÖ3x + C4e-Ö3x
Контрольные задания
Решить уравнения
27.1 y²¢ - 9y² + 28y¢ - 30y = 0; y² - 4y¢ - 5y = -5x + 2
27.2 y²¢ - 8y² + 14y¢ + 68y = 0; y² - y¢ - 20y = -3x - 1
27.3 y²¢ - y² + 24y¢ + 26y = 0; y² - 8y¢ + 15y = 2x - 5
27.4 y²¢ - 8y² + 9y¢ + 58y = 0; y² - 25y = 2x + 5
27.5 y²¢ - 3y² + 4y¢ - 2y = 0; y² + 6y¢ + 8y = -5x + 1
27.6 y²¢ - 3y² - 8y¢ + 30y = 0; y² - 7y¢ + 10y = -5x + 5
27.7 y²¢ - y² - 5y¢ + 125y = 0; y² + 3y¢ - 10y = -3x + 3
27.8 y²¢ + 9y² + 16y¢ - 26y = 0; y² - y¢ - 2y = 3x - 5
27.9 y²¢ + 6y² + y¢ - 34y = 0; y² + 7y¢ + 12y = 5x - 1
27.10 y²¢ - 5y² - 7y¢ + 51y = 0; y² - y¢ - 12y = 3x + 2
27.11 y²¢ + 3y² + 7y¢ - 75y = 0; y² - 6y¢ + 8y = -5x + 2
27.12 y²¢ - 13y² + 56y¢ - 78y = 0; y² - 4y¢ - 5y = -5x + 3
27.13 y²¢ + 15y² + 100y¢ + 250y = 0; y² - 9y¢ + 20y = -5x - 4
27.14 y²¢ + 4y² + 6y¢ + 4y = 0; y² + 4y¢ - 5y = -3x - 1
27.15 y²¢ + 12y² + 57y¢ + 100y = 0; y² - 16y = 5x + 1
27.16 y²¢ + y² + 4y¢ + 30y = 0; y² - 6y¢ + 8y = -3x - 4
27.17 y²¢ - 4y² - 15y¢ + 68y = 0; y² - y¢ - 6y = 2x - 4
27.18 y²¢ + 7y² + 20y¢ + 50y = 0; y² - 9y = -3x + 3
27.19 y²¢ + 6y² + 18y¢ + 40y = 0; y² - 9y = -3x + 2
27.20 y²¢ - 13y² + 65y¢ - 125y = 0; y² + 2y¢ - 15y = 5x - 3
27.21 y²¢ - 8y² + 30y¢ - 36y = 0; y² - 2y¢ - 15y = -5x - 2
27.22 y²¢ + 7y² - y¢ - 87y = 0; y² + 4y¢ + 3y = -3x + 1
27.23 y²¢ + 10y² + 49y¢ + 100y = 0; y² - 2y¢ - 3y = -5x + 2
27.24 y²¢ - 8y² + 22y¢ - 20y = 0; y² - 2y¢ - 3y = 4x + 3
27.25 y²¢ + 7y² + 27y¢ + 85y = 0; y² - 7y¢ + 12y = 4x + 5
27.26 y²¢ + 2y² - 16y = 0; y² - 5y¢ + 6y = -3x - 5
27.27 y²¢ + 11y² + 43y¢ + 65y = 0; y² - 6y¢ + 8y = -2x + 5
27.28 y²¢ + 7y² + 12y¢ + 10y = 0; y² - 16y = -5x + 1
27.29 y²¢ + 7y² + 41y¢ + 87y = 0; y² - 8y¢ + 15y = 3x - 2
27.30 y²¢ - 10y² + 48y¢ - 64y = 0; y² - y¢ - 2y = -4x - 4
27.31 y²¢ - 5y² + 7y¢ + 13y = 0; y² - y¢ - 20y = -5x - 2
27.32 y²¢ + 3y² + 16y¢ - 20y = 0; y² - y¢ - 12y = -3x + 1
27.33 y²¢ - 7y² + 25y¢ - 39y = 0; y² - y¢ - 12y = -3x + 3
27.34 y²¢ - 3y² - 8y¢ + 30y = 0; y² + 3y¢ + 2y = 3x + 4
27.35 y²¢ + 6y² + 18y¢ + 40y = 0; y² - y¢ - 12y = 4x + 2
