9. Функции нескольких аргументов.

Рассмотрим множество A пар действительных чисел (x,y). Говорят, что на множестве A задана функция (двух аргументов) f, если задано соответствие по которому каждому элементу множества A (область определения) соответствует единственный элемент числового множества B (множество значений). Символически это записывается так: f:A®B. Здесь f - функция, A - область определения, B - множество значений. В привычной записи z=f(x,y), где z - функция, x и y - её аргументы. Функции двух аргументов могут быть заданы формулами, таблицами или графически.

Примеры.

Задание формулой: z=x^y; z=x²y³; z=log_xy и т.д.

Задание таблицей (первый вариант)

x	1	1	1	2	2	2	3	3	3
y	1	2	3	1	2	3	1	2	3
f(x,y)	1	3	6	9	8	5	-1	-5	-10

Задание таблицей (второй вариант)

y x	1	2	3
1	1	9	-1
2	3	8	-5
3	6	5	-10

Графическое задание имеет два варианта: в виде рисунка поверхности; в виде изолиний (линий равного уровня)

Аналогично функциям двух аргументов можно рассматривать функции трёх, четырёх и большего числа аргументов.

666

Построить изолинии:

1. z = x² + 4y² 2. z = xy

3. z = x^y 4. z = y² - 4x

555

Частные производные и полный дифференциал функции нескольких аргументов.

Частной производной функции z = f(x,y) по x называется обычная производная при условии, что y - постоянная и аналогично - частная производная по y. Они обозначаются так:

или: или: z¢_x и z¢_y или: f¢_x(x,y) и f¢_y(x,y)

Полным дифференциалом называется выражение: dz = z¢_xdx + z¢_ydy

666

Найти частные производные первого порядка и полные дифференциалы:

5. z = x^y 6. z = xsiny + ycosx

7. z = ln(x+y) + ln(x-y) 8. z = xe^y + ye^x

Найти частные производные второго порядка:

9. z = sin(x+2y) 10. z = y^-x

11. z = xlny + ylnx 12. z = x³ + 3xy + y³

555

Экстремум функции нескольких аргументов.

Если в некоторой окрестности точки (x₀,y₀) выполняется условие f(x,y)<f(x₀,y₀), то (x₀,y₀) называется точкой максимума, а если f(x,y)>f(x₀,y₀), то (x₀,y₀) называется точкой минимума. Максимум и минимум называются экстремумами.

Необходимые условия экстремума:

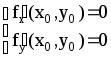
Достаточные условия экстремума:

Обозначим A = f²_xx(x₀,y₀), B = f²_xy(x₀,y₀), C = f²_yy(x₀,y₀).

Если B² -4AC<0, то в точке (x₀,y₀) минимум при A>0 и максимум при A<0.

Если B² -4AC>0, то в точке (x₀,y₀) экстремума нет

666

Найти экстремумы:

13. z = x² + y² + xy - 4x - 5y 14. z = xy(1 - x - y)

15. z = x³ - y³ - 3xy 16. z = xy+

555

Основные операции над скалярным и векторным полями.

Скалярным полем называется функция двух или трёх аргументов. Векторным полем называется вектор, у которого координаты - функции нескольких аргументов.

Оператором набла называется символическое выражение: Ñ = ()

Выражение Ñf(x,y,z) называется градиентом скалярного поля f.

Выражение Ñ×F(x,y,z) называется дивергенцией векторного поля F.

Выражение Ñ´F(x,y,z) называется ротором векторного поля F.

Выражение u¢_n = Ñu×n/n называется производной по направлению n.

666

Найти градиент:

17. u = xyz Решение: Ñu = (yz, xz, xy)

18. u = 19. u = x^y + y^z + z^x

Найти дивергенцию и ротор векторного поля F:

20. F = (x², y², z²)

Решение: Ñ×F = 2x + 2y + 2z Ñ´F =

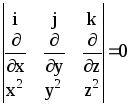
21. F = (x+y, y+z, z+x) 22. F = (x^y, y^z, z^x)

Найти производную по направлению n:

23. u = xyz, n = (3,4,-12)

Решение: Ñu = (yz, xz, xy) Þ u¢_n = (3yz + 4xz - 12xy)/13;

24. u = (x-y)(y-z)(z-x), n = (4,3,12) 25. u = x² + y² + z², n = (1,1,1)

555

Линейный регрессионный анализ.

Пусть дана таблица вида:

n	1	2	3	...	N
xn	x1	x2	x3	...	xN
yn	y1	y2	y3	...	yN

Требуется найти зависимость вида y_n=ax_n+b. Для этого строим таблицу:

n	1	2	3	...	N	S0=N
xn	x1	x2	x3	...	xN	S1
yn	y1	y2	y3	...	yN	S01
xn2	x12	x22	x32	...	xN2	S2
xnyn	x1y1	x2y2	x3y3	...	xNyN	S11

В последнем столбце таблицы пишем суммы элементов строк.

Тогда для a и b получаем систему: 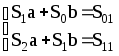, которая даст решение задачи.

666

26. По таблице найти зависимость y=ax+b:

n	1	2	3	4
xn	1	2	3	4
yn	2	5	7	8

Решение. Составим таблицу:

n	1	2	3	4	4
xn	1	2	3	4	10
yn	2	5	7	8	22
xn2	1	4	9	16	30
xnyn	2	10	21	32	65

Получаем систему: 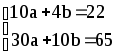Þ

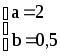
Ответ: y=2x+0,5

27. По таблице найти зависимость y=ax+b:

n	1	2	3	4	5	6
xn	1	2	3	4	5	6
yn	4	9	10	15	16	21

555

Правила приближённых вычислений.

Обозначим через Da максимум модуля погрешности величины a. Тогда справедливы правила:

1) D(a±b) = Da + Db

2) D(ab) = |a|Db + |b|Da

3) D =

4) Df(a) = |f¢(a)|Da

5) Df(a,b) = |f¢_a(a,b)| Da + |f¢_b(a,b)| Db

При вычислениях следует сохранять одну запасную десятичную цифру.

В погрешности следует оставлять не более двух значащих цифр.

666

28. Найти погрешность вычисления приa»1, b»9, Da=0,1 Db=0,2

29. Найти погрешность вычисления приa»3, b»4, Da=0,01 Db=0,02

30. Найти погрешность вычисления площади треугольника, если a»10, b»10, с»10, Da=Db=Dс=0,1

555

Ответы:13. z_min=-7 в точке (1;2) 14. нет 15. z_max=1 в точке (-1;1)

16. z_min=6 в точке (0,5;4) 27. y=3x+2 29. 0,022

Контрольные задания.

Найти экстремумы функции z

24.1 z = -5x² - xy - 4y² - 58x + 34y + 4

24.2 z = 4x² + 3xy + y² + 52x + 34y

24.3 z = 3x² + 2xy + 8y² + 120y - 1

24.4 z = -2x² - 3xy - 4y² - 10x - 16y + 9

24.5 z = x² + xy + xy + 9y² - 48y + 8

24.6 z = 5x² - xy + 9y² + 48x + 96y - 6

24.7 z = -8x² + xy + xy - y² - 18x + 18y + 7

24.8 z = 8x² + 7xy + 6y² - 136x - 118y - 2

24.9 z = -8x² - 8xy - 5y² - 16x + 2y - 3

24.10 z = -5x² - 4xy - 8y² - 96x - 144y - 8

24.11 z = 2x² - 3xy + 8y² - 28y - 9

24.12 z = 5x² + 9xy + 7y² + 78x + 122y - 4

24.13 z = -7x² - 5xy - 3y² - 134x - 90y + 3

24.14 z = 7x² - 6xy + 5y² + 8x - 8y + 9

24.15 z = -8x² - 8xy - 9y² - 144x - 156y - 6

24.16 z = -x² - xy - y² + 4x + 4y + 8

24.17 z = -x² - xy - y² + 2x + 2y

24.18 z = -5x² + 9xy - 7y² - 142x + 182y + 7

24.19 z = -5x² - 6xy - 7y² - 58x - 66y - 3

24.20 z = 6x² - 5xy + 4y² + 46x - 38y - 2

24.21 z = -8x² + 3xy - 3y² + 102x - 42y - 2

24.22 z = -6x² + 5xy - 5y² + 18x - 30y + 7

24.23 z = -6x² - 6xy - 5y² - 60x - 62y + 1

24.24 z = -x² + 2xy - 2y² - 4x + 8y + 4

24.25 z = 3x² + 3xy + y² + 24x + 28y - 6

24.26 z = -3x² + xy + xy - 4y² - 26x + 38y + 3

24.27 z = 4x² + 7xy + 7y² + 50x + 98y - 7

24.28 z = 3x² + 4xy + 2y² + 110x + 100y - 8

24.29 z = 2x² - 3xy + 2y² - 46x + 34y + 3

24.30 z = -7x² - 5xy - 9y² + 20x - 40y - 3

24.31 z = 2x² + 6xy + 5y² + 28x + 84y + 1

24.32 z = -x² + 2xy - 7y² + 8x - 4y - 5

24.33 z = -8x² - 8xy - 3y² + 30y + 3

24.34 z = -4x² - 6xy - 3y² - 72x - 108y + 9

24.35 z = 8x² - 2xy + 7y² + 72x + 8y - 6

------------

25.1 У треугольника сумма двух сторон 10см. Найти наибольшую площадь такого треугольника.

25.2 У прямоугольника сумма трёх сторон 15см. Найти наибольшую площадь такого прямоугольника.

25.3 У прямоугольного параллелепипеда сумма площадей пяти граней 100см². Найти наибольший объём такого параллелепипеда.

25.4 У прямого цилиндра боковая площадь 100см². Найти наибольший объём такого цилиндра.

25.5 У прямого кругового конуса площадь боковой поверхности 200см². Найти наибольший объём такого конуса.

25.6 У прямого усечённого кругового конуса площадь боковой поверхности 200см², отношение диаметров оснований 2. Найти наибольший объём такого конуса.

25.7 У треугольника сумма двух сторон 30см. Найти наибольшую площадь такого треугольника.

25.8 У прямоугольника сумма трёх сторон 45см. Найти наибольшую площадь такого прямоугольника.

25.9 У прямоугольного параллелепипеда сумма площадей пяти граней 300см². Найти наибольший объём такого параллелепипеда.

25.10 У прямого цилиндра боковая площадь 300см². Найти наибольший объём такого цилиндра.

25.11 У прямого кругового конуса площадь боковой поверхности 600см². Найти наибольший объём такого конуса.

25.12 У прямого усечённого кругового конуса площадь боковой поверхности 400см², отношение диаметров оснований 3. Найти наибольший объём такого конуса.

По таблице найти линейную зависимость вида y = ax + b

26.1 x -1 0 1 2 3

y -24 3 30 57 84

26.2 x -1 0 1 2 3 4

y 3 11 19 27 35 43

26.3 x 2 3 4 5 6 7 8

y 28 1 -26 -53 -80 -107 -134

26.4 x -4 -3 -2 -1 0

y 108 100 92 84 76

26.5 x 0 1 2 3 4

y -4 -31 -58 -85 -112

26.6 x -5 -4 -3 -2 -1 0

y 4 3 2 1 0 -1

26.7 x 5 6 7 8 9

y 620 745 870 995 1120

26.8 x -2 -1 0 1 2 3 4

y -249 -124 1 126 251 376 501

26.9 x 3 4 5 6 7 8

y -348 -473 -598 -723 -848 -973

26.10 x 5 6 7 8 9 10

y -315 -379 -443 -507 -571 -635

26.11 x -3 -2 -1 0 1 2 3

y 14 15 16 17 18 19 20

26.12 x 2 3 4 5 6 7

y -121 -185 -249 -313 -377 -441

26.13 x 3 4 5 6 7 8

y 383 508 633 758 883 1008

26.14 x -3 -2 -1 0 1 2 3

y 96 88 80 72 64 56 48

26.15 x -5 -4 -3 -2 -1 0 1

y 136 109 82 55 28 1 -26

26.16 x 3 4 5 6 7 8

y 412 537 662 787 912 1037

26.17 x -5 -4 -3 -2 -1 0

y -77 -50 -23 4 31 58

26.18 x -2 -1 0 1 2 3

y 59 32 5 -22 -49 -76

26.19 x 2 3 4 5 6

y 4 3 2 1 0

26.20 x 5 6 7 8 9 10 11

y 317 381 445 509 573 637 701

26.21 x 5 6 7 8 9 10 11

y -7 -8 -9 -10 -11 -12 -13

26.22 x -3 -2 -1 0 1 2 3

y 35 43 51 59 67 75 83

26.23 x 3 4 5 6 7

y 203 267 331 395 459

26.24 x 0 1 2 3 4

y 0 -64 -128 -192 -256

26.25 x 3 4 5 6 7 8 9

y 198 262 326 390 454 518 582

26.26 x -5 -4 -3 -2 -1 0 1

y 628 503 378 253 128 3 -122

26.27 x 4 5 6 7 8 9 10

y 181 208 235 262 289 316 343

26.28 x 1 2 3 4 5

y 150 275 400 525 650

26.29 x 0 1 2 3 4 5

y 4 -60 -124 -188 -252 -316

26.30 x -4 -3 -2 -1 0 1

y -2 -1 0 1 2 3

26.31 x -1 0 1 2 3 4

y -54 10 74 138 202 266

26.32 x -5 -4 -3 -2 -1 0

y -135 -108 -81 -54 -27 0

26.33 x -3 -2 -1 0 1 2 3

y 262 198 134 70 6 -58 -122

26.34 x -3 -2 -1 0 1

y 59 58 57 56 55

26.35 x -4 -3 -2 -1 0

y 326 262 198 134 70

Найти погрешность вычислений по формуле:

27.1 , если a»50, b»100, Da=1, Db=2

27.2 , если a»50, b»100, Da=1, Db=2

27.3 , если a»50, b»100, Da=1, Db=2

27.4 , если a»50, b»100, Da=1, Db=2

27.5 , если a»50, b»100, Da=1, Db=2

27.6 , если a»50, b»150, Da=1, Db=2

27.7 , если a»50, b»150, Da=1, Db=2

27.8 , если a»50, b»150, Da=1, Db=2

27.9 , если a»50, b»150, Da=1, Db=2

27.10 , если a»50, b»150, Da=1, Db=2

27.11 , если a»150, b»100, Da=3, Db=2

27.12 , если a»150, b»100, Da=3, Db=2

27.13 , если a»150, b»100, Da=3, Db=2

27.14 , если a»150, b»100, Da=3, Db=2

27.15 , если a»150, b»100, Da=3, Db=2

27.16 , если a»50, b»200, Da=3, Db=2

27.17 , если a»50, b»200, Da=3, Db=2

27.18 , если a»50, b»200, Da=3, Db=2

27.19 , если a»50, b»200, Da=3, Db=2

27.20 , если a»50, b»200, Da=3, Db=2

27.19 , если a»50, b»200, Da=3, Db=2

27.20 , если a»50, b»200, Da=3, Db=2

27.21 , если a»250, b»100, Da=1, Db=3

27.22 , если a»250, b»100, Da=1, Db=3

27.23 , если a»250, b»100, Da=1, Db=3

27.24 , если a»250, b»100, Da=1, Db=3

27.25 , если a»250, b»100, Da=1, Db=3

27.26 , если a»250, b»100, Da=1, Db=3

27.27 , если a»250, b»100, Da=1, Db=3

27.28 , если a»250, b»100, Da=1, Db=3

27.29 , если a»250, b»100, Da=1, Db=3

27.30 , если a»250, b»100, Da=1, Db=3

27.31 , если a»75, b»100, Da=4, Db=2

27.32 , если a»75, b»100, Da=4, Db=2

27.33 , если a»75, b»100, Da=4, Db=2

27.34 , если a»75, b»100, Da=4, Db=2

27.35 , если a»75, b»100, Da=4, Db=2