Добавил:

Artyom Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Novikontas Maritime College

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Geophysics Methods Костицын В. И

..pdf

Скачиваний:

Добавлен:

03.05.2023

Размер:

6.07 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 415 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

							Гравиразведка

g	G(		)		V	(z z) ,	(1.21
g	G(	0	)			(z z) ,	)
		0			r 3		)
где (	0 )	– избыточная (аномальная) плотность.
При	0			g имеет положительный знак, т.е. наблюда-
ется увеличение притяжения, аномалии							g положительны. При
0	g имеет отрицательный знак, т.е. наблюдается умень-
шение притяжения, аномалии g отрицательны.

В принципе аномалия, созданная любым телом, может

быть определена интегралом по объему тела:
gV G(	0 )		(z	z)	V	,	(1.2
							2)
		V		r 3			2)
		V

т.е. суммой притяжений всех элементарных объемов, из которых состоит тело.

1.9. Прямая и обратная задачи для шара

1. Прямая задача. Пусть однородный шар радиусом и плотностью расположен на глубине h в среде с плотностью 0 (для простоты центр находится на оси z, а наблюдения проводятся по оси x в точке P) (рис. 1.2).

Формула для вычисления g может быть получена из (1.19

– 1.22) путем замены элемента dm массой шара в силу того, что притяжение однородным шаром происходит так, как если бы вся масса была сосредоточена в центре шара. Учитывая, что x' = y' = 0, z' = h, y = z = 0, получим формулу для шара:

g GM	h	G(		)V	h	G(		)Vh /(x2 h2 )	32
	r 3		0		r 3		0		(1.23)

График g будет иметь максимум над шаром (x = 0) и асимптотически стремиться к нулю при удалении от шара. В

В.К. Хмелевской, В.И. Костицын

плане изолинии g будут иметь вид концентрических окружностей.

Вторая производная (градиент аномалии по профилю наблюдений) равна

W		( g)	GMh (1/ r 3 ) / x 3GMhx/ r 5 .	(
	xz	x		1.24)

Вид кривой Wxz может быть легко получен путем графического построения из кривой g. График Wxz имеет перед шаром максимум, за шаром – минимум, над центром шара – ноль.

Рис.1.2. Гравитационное поле шара

2. Обратная задача. В соответствии с формулой (1.23) максимум g над центром шара (x = 0) равен gмах = E = GM/h2.

Для точки, удаленной от максимума на расстояние x1/2, имеющей g1/2 = 1/2 E, можно записать следующее уравнение:

g	GM	GMh	или	2h3 x2	h2 3 2 .

1 2	2h2	x122 h2 3 2		1 2

Гравиразведка

Решив последнее уравнение, получим формулу для определения глубины залегания центра шара:

h 1,305x1 2 .

(1.25)

Зная h, легко найти избыточную массу (M):

M E h2 /G .

(1.26)

Так как M V 43 R3 , то, зная аномальную плотность 0 , можно рассчитать объем (V) и радиус шара (R). Так, радиус равен

R 3,3 3	Eh2	(1.27)
	,

где E – в миллигалах, h – в метрах, – в г/см3.

1.10. Прямая и обратная задачи для горизонтального бесконечно длинного кругового цилиндра

1. Прямая задача. Рассмотрим бесконечно длинный круговой горизонтальный цилиндр радиусом R, расположенный вдоль оси y (рис. 1.3). Ось наблюдений (x) направим вкрест простирания цилиндра.

Притяжение однородным цилиндром происходит так же, как если бы вся его масса была сосредоточена вдоль вещественной линии, расположенной вдоль оси цилиндра, с массой еди-

ницы длины, равной		dm / dy	R2 (	0	) . Используя фор-
мулу (1.22), можно получить выражения для					g и Wxz:
g Gh		y	2Gh R2 (		0 )	,	(1.28)
	(x2	y 2 z 2 )3 / 2	x2 h2

							41

В.К. Хмелевской, В.И. Костицын

W	(	g)	4Gh x		.	(1.29)

	xz	z	(x2	h2 )2

Рис.1.3. Гравитационное поле бесконечно длинного кругового горизонтального цилиндра

Графики g и Wxz над шаром и цилиндром внешне похожи (см. рис. 1.2 и 1.3). В плане изолинии g над цилиндром будут вытянутыми параллельными линиями.

2. Обратная задача. Из формул (1.22) и (1.28, 1.29) мож-

но при х = 0 получить

gm ax	2G / h .				(1.30)
Отсюда
g1 2	gmax / 2	G		2G h

		2		(x	h2 )
			1 2

h2 x122 ,

x1 2 ,

(1.31)

Гравиразведка

т.е. глубина залегания цилиндра равна расстоянию от точки

максимума gmax до точки, где g gmax / 2 .

Определив h и зная избыточную плотность, можно рассчитать

R2 (

0 ) 0,0075h gmax

(1.32)

и радиус цилиндра:

R	0,0075h	gm ax	.	(1.33)
	(	0 )

Зная R, можно получить глубины залегания верхней hв= h

– R и нижней hн= h + R кромок цилиндра Wxz .

1.11. Прямая и обратная задача для вертикального уступа (сброса)

1. Прямая задача. Пусть вертикальный уступ (сброс) простирается бесконечно вдоль оси y (рис. 1.4). Наблюдения производятся вдоль оси (x), (y = z = 0), расположенной вкрест простирания сброса. Если глубина до кровли z1 и z2 , а амплитуда уступа h, то, согласно (1.22)

		z2	dz
g G(	0 ) dx dy		dz				.	(1.34)

		z (x x)2	y 2		2	3 2
	0	z (x x)2	y 2	z	2
		1

В общем случае выражение интеграла имеет громоздкий вид. В частности, полная максимальная аномалия над уступом (разность силы тяжести между поднятым и опущенным крылом) определится следующей формулой:

gm ax 2 G(

0 ) (z2 z1 ) .

(1.35)

В.К. Хмелевской, В.И. Костицын

Над уступом (при x = 0) аномалия равна половине максимальной величины.

Рис.1.4. Гравитационное поле над уступом (сбросом)

2. Обратная задача. Из формулы (1.35) можно опреде-

лить h z2 z1	gm ax / 2 G(	0 ) .
В теории гравиразведки доказано, что примерная глубина
расположения середины высоты уступа (H				(z2	z1 ) / 2) равна
x1/2, т.е. абсциссе точки, в которой			g1 2	g0 /2	gm ax/4 , где
g0 – аномалия над уступом, а		gmax – полная аномалия. Прак-
тически для определения H на кривой			g находится местополо-

жение сброса (Δg0) и в масштабе профиля рассчитывается x1/2 –

расстояние от сброса до точки, в которой g =	g0/2. Зная H и h,
легко определить глубины до приподнятого	(z1 H h / 2) и
опущенного (z2 H h / 2) крыла.

1.12. Графическое определение аномалий силы тяжести двухмерных тел с помощью палетки Гамбурцева

1. Прямая задача. Для тел более сложной формы расчет g представляет большие трудности и выполняется либо на компьютерах, либо графическим путем с помощью различных палеток. Для вычислений аномалий над телами с сечением любой произвольной формы, вытянутыми вдоль оси (двухмерные

тела), применяется палетка Гамбурцева (рис. 1.5).

Гравиразведка

Рис.1.5. Палетка Гамбурцева для вычисления притяжения двухмерных тел

Здесь из точки О через один и тот же угол φ проведены

радиусы, а через равные расстояния			z – параллельные линии.
Сила тяжести g в точке О за счет притяжения бесконеч-
ной горизонтальной призмой с сечением в виде трапеции ABCD
одинакова для любой из таких призм и равна
gп 2G(	0 )	z .	(1.36)

В самом деле, воспользуемся формулой притяжения бесконечно длинным цилиндром (1.28, 1.29), в которую вместо λ подставим массу элементарной призмы сечением dxdz:

R2 (

0 ) .

(1.37)

Притяжение бесконечно длинной призмой любого сечения может быть рассчитано по формуле

	g	2G(		0 )		z			dxdz .	(1.38)

					x	2	z	2
					x		z
	Заменив		x	z ctg		,		получим x		z( 1/ sin 2 ) d , но
sin 2	z 2 /(x2		z 2 ) , поэтому
	g	2G(		0 )		z
										(1.39)
	2G(		0 )	z					g П ,
										45

В.К. Хмелевской, В.И. Костицын

где	gП	– цена		одной	трапеции	(цена	палетки), рав-
ная	gП	2G	П	z .
	Подобрав		g,	и	z такими,	чтобы	gП равнялось ка-

кому-нибудь постоянному значению (например 0,01 мГал), легко рассчитать в точке О аномалию от призмы любого сечения, для чего надо подсчитать число трапеций, покрывающих сече-

ние исследуемого тела (n). Аномалия				g равна n, умноженному
на цену палетки и масштабный коэффициент
K	П	M П	,	(1.40)

	0	M Р

где П и МП – избыточная (аномальная) плотность и масштаб палетки, а 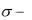0 и МР – избыточная (аномальная) плотность и

масштаб геологического разреза.

Таким образом, аномалия над двухмерным телом любого сечения с помощью палетки Гамбурцева рассчитывается по

формуле
g n gП K .	(1.41)

2. Обратная задача. Используя формулу (1.41), с помощью палетки Гамбурцева можно выяснить форму и положение сечения возмущающего двухмерного аномалиесоздающего объекта. Для этого надо знать избыточную плотность 0 , оце-

нить аналитическим способом положение ее центра и для нескольких точек графика g построить возможные сечения возмущающего тела. Среднее из них характеризует примерное сечение тела.

1.13. Численные методы решения прямых и обратных задач гравиразведки

Для более сложных форм аномалиеобразующих объектов прямые задачи гравиразведки решаются численными методами с помощью ЭВМ. За основу берется формула (1.22) для гравита-

Гравиразведка

ционной аномалии, созданной любым телом с постоянной или переменной избыточной плотностью. Практически численный метод сводится к разбивке объекта на элементарные массы, ячейки, например, шаровой или кубической формы. Гравитационный эффект таких масс рассчитывается по формуле (1.21), а затем ведется их суммирование по всему объему объекта.

На рис. 1.6 приведен схематический пример того, как тела разного сечения и глубины залегания даже при постоянной избыточной плотности могут создавать одинаковую аномалию силы тяжести.

Обратные задачи решаются методом сравнения полевой аномалии с теоретически рассчитанными аномалиями, у которых геометрические параметры и избыточные плотности постепенно изменяются до получения наименьших расхождений между кривыми. Если прямые задачи, как и всякие прямые задачи математической физики, однозначны, то обратные задачи неоднозначны.

Рис.1.6. К неоднозначности решения обратной задачи гравиразведки

1.14. Принципы измерений силы тяжести и гравиметрическая аппаратура

Основным измеряемым параметром в гравиразведке является ускорение силы тяжести g, которое определяется либо абсолютно, либо относительно. При абсолютных измерениях получают полное (наблюденное) значение ускорения gн, при относительных – его приращение относительно некоторой исходной точки gн.

В.К. Хмелевской, В.И. Костицын

Методы измерения ускорения силы тяжести и его приращения делятся на динамические и статические. Под динамическими понимаются такие методы, при которых наблюдается движение тела под действием силы тяжести (качание маятника, свободное падение тел и др.) В этом случае g определяется через параметры движения тела и параметры установки. При статических методах действие силы тяжести компенсируется (например силой упругости пружины), а g определяется по изменению статического положения равновесия тела.

Реже в гравиразведке измеряются вторые производные гравитационного потенциала Wxy , Wxz , Wyz , (Wyy Wxx ) .

1.14.1. Динамические методы

Из динамических методов наиболее широко применяется

маятниковый метод. Для абстрактного объекта (математи-

ческого маятника) период колебаний определяется по формуле

		1	sin 2		9	sin 4		(1.4
T	l g (1			/ 2			/ 2) ,
		4			64			2)

где l – длина	маятника, g – ускорение силы тяжести,							– макси-

мальное значение угла отклонения маятника от вертикали. Эта формула остается справедливой и для реального объекта (физического маятника), если в качестве l взять так называемую приведенную длину l Jma , где J – момент инерции маятника, m – масса, – расстояние от центра тяжести до оси вращения. При малых a формула для периода принимает вид

T 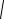lg . (1.43)

Точность определения периода возрастает при увеличении времени наблюдения за колебаниями маятника. Для абсолютных измерений ускорения силы тяжести необходимо измерять

длину маятника. Зная g0, тогда T0 lg0 будет на исходной

<<< < Предыдущая 1 2 3 45 / 415 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>