
лекции / DSP_9
.pdf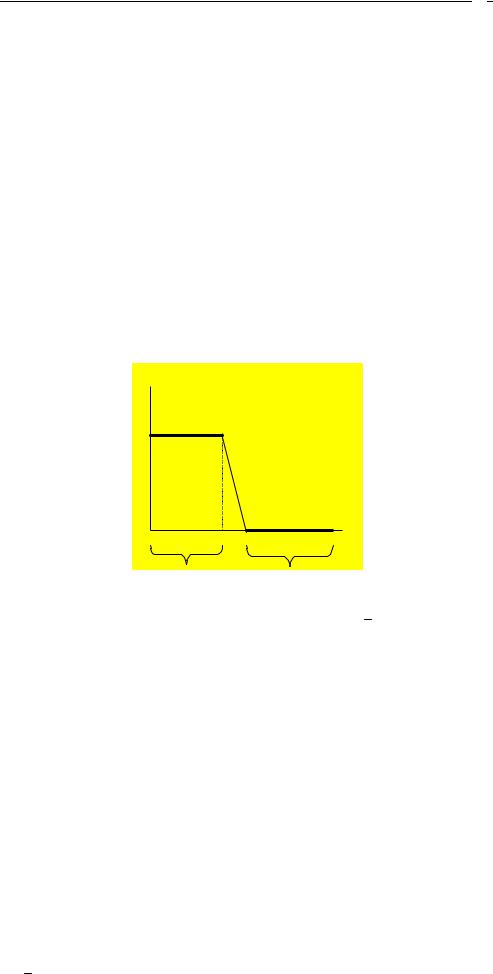
1
Лекция 9. Синтез КИХ-фильтров методом наилучшей равномерной (чебышевской) аппроксимации
1.Синтез КИХ-фильтров методом наилучшей равномерной (чебышевской) аппроксимации.
2.Теорема Чебышева и следствия из нее.
3.Итерационная процедура синтеза оптимального КИХ-фильтра.
9.1. Синтез КИХ-фильтров методом наилучшей равномерной (чебышевской) аппроксимации
Постановка задачи: синтезировать оптимальный КИХ-фильтр с ЛФЧХ.
Оптимальный КИХ-фильтр — это КИХ-фильтр минимально возможного порядка при заданных требованиях к АЧХ.
Рассмотрим метод наилучшей равномерной (чебышевской) аппроксимации в приложении к синтезу КИХ-фильтра:
1.Задание аппроксимируемой функции.
При синтезе КИХ-фильтра — это идеальная АЧХ в ПП и ПЗ.
Проиллюстрируем на примере ФНЧ.
Аппроксимируемая АЧХ — непрерывная функция ( ) (рис. 9.1).
1
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
k |
|
|
|
||
|
|
|
2 |
||||||
1 |
|
|
|
|
|
|
|
||
Рис. 9.1. АЧХ идеального КИХ-фильтра ФНЧ |
|
||
2. Выбор класса аппроксимирующих функций. |
|
||
В табл. Лекции 7 приведены амплитудные функции B( , |
a |
) |
КИХ-фильтров 4-х |
типов — тригонометрические полиномы. Поэтому |
выбираем класс |
||
аппроксимирующих функций — тригонометрический полином.
3.Выбор аппроксимирующей функции.
Аппроксимирующая функция выбирается в заданном классе и зависит от типа КИХ-фильтра.
Например, для КИХ-фильтра 1-го типа аппроксимирующая функция имеет следующий вид тригонометрического полинома (см. табл. в Лекции 7):
|
|
|
M |
a |
|
|
|
, |
(9.1) |
||
B( , a) |
|
cos M k |
|||||||||
|
|
|
k |
|
|
|
|
|
|||
|
|
|
k 0 |
|
|
|
|
|
|
|
|
где M — порядок полинома: |
|
|
|
|
|
|
|
|
|
||
|
|
M |
R |
|
N 1 |
, |
|
|
(9.2) |
||
|
|
2 |
|
|
|
||||||
|
|
|
|
|
2 |
|
|
|
|
||
R — порядок КИХ-фильтра. |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
R 2M , |
|
|
(9.3) |
||||
N – длина КИХ-фильтра: |
|
|
|
|
|
|
|
|
|
||
|
|
|
N 2M 1; |
|
|
(9.3) |
|||||
a вектор неизвестных коэффициентов полинома ak .

|
|
|
|
|
|
|
|
|
|
|
|
2 |
||
АЧХ A( ) |
КИХ-фильтра — это модуль его амплитудной функции B( , |
a |
): |
|||||||||||
|
|
|
|
|
|
|
|
. |
(9.4) |
|||||
|
|
|
|
|
|
|||||||||
|
A( ) |
|
B( , a) |
|||||||||||
Синтез КИХ-фильтра сводится к расчету его импульсной характеристики. |
||||||||||||||
Поскольку в данном случае ИХ |
|
h(n)связана линейно с коэффициентами ak |
||||||||||||
(см. табл. в Лекции 7): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
h(M k), |
k M; |
|||||||||
|
ak |
|
|
|||||||||||
|
2 |
|||||||||||||
|
|
|
|
|
|
|
|
(9.5) |
||||||
|
|
|
|
|
|
|
|
|
|
k M, |
||||
|
|
h(k), |
|
|
|
|
||||||||
в методе чебышевской аппроксимации синтез КИХ-фильтра сводится к расчету вектора a .
4.Выбор полинома B( , a) наилучшего приближения к аппроксимируемой функции ξ(ω).
В качестве критерия наилучшего приближения аппроксимирующей функции — тригонометрического полинома B( , a) — к аппроксимируемой функции ( )
выбран минимум максимума взвешенной ошибки аппроксимации:
max |
|
|
|
|
|
|
|
|
min |
, |
(9.6) |
( ,a) |
max p( ) |
( ) B( ,a) |
|||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где:
p( ) — весовая функция;
( ,a) — взвешенная ошибка аппроксимации;
— интервал аппроксимации — совокупность всех ПП и ПЗ; в примере для ФНЧ это совокупность ПП 1 и ПЗ ФНЧ 2 (см. рис.9.1).
Критерий (9.6) называют минимаксным, а также равномерным или критерием Чебышева.
Согласно критерию (9.6), полиномом наилучшего приближения B( , a)
обеспечивает минимальную максимальную (по модулю) взвешенную ошибку аппроксимации на интервале аппроксимации .
В переходных полосах ошибка аппроксимации не контролируется.
Решение задачи аппроксимации сводится к поиску вектора коэффициентов a полинома наилучшего приближения B( , a).
Весовая функция p( ) управляет значением модуля максимума ошибки
аппроксимации на интервале аппроксимации и рассчитывается следующим образом:
вес, равный 1, присваивается полосе с наибольшим отклонением;
веса в остальных полосах определяются как отношение максимального отклонения к отклонению в данной полосе.
Пример 9.1
Для ФНЧ заданы максимально допустимые отклонения в ПП 1 0,05 и в ПЗ
2 0,01. Определить весовую функцию p( ).
Вес, равный 1, присваивается ПП.
ВПЗ вес определяется как отношение 1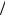 2 5:
2 5:
1, ПП p( )
5, ПЗ
9.2.Теорема Чебышева и следствия из нее
Теорема Чебышева.

3
Для того чтобы тригонометрический полином B( ,a) порядка M был полиномом наилучшего равномерного приближения непрерывной функции ξ(ω) на интервале
, необходимо и достаточно, чтобы максимальная по модулю взвешенная ошибка аппроксимации на этом интервале достигалась не менее чем в (M 2) точках и последовательно чередовалась по знаку.
Теорему Чебышева называют теоремой об альтернансе — чередование противоположных.
Следствия из теоремы Чебышева:
1.Полином наилучшего приближения определяется среди полиномов одинакового порядка M .
2.Существует единственный полином наилучшего приближения порядка M , который обеспечивает минимальную максимальную взвешенную ошибку аппроксимации.
3.Существует единственный полином наилучшего приближения, который при заданной максимальной взвешенной ошибке аппроксимации обеспечивает
минимальный порядок полинома M , а следовательно, минимальный порядок КИХ-фильтра.
4.Частоты, на которых модуль взвешенной ошибки аппроксимации достигает своего максимума, называют частотами (или точками) альтернанса; их количество m равно:
m M 2 |
. |
(9.7) |
5.Чередование противоположной по знаку максимальной ошибки аппроксимации позволяет записать критерий Чебышева (9.6) для частот альтернанса i в виде
(для простоты p( ) 1): |
|
|
|
|
|
|
|
|
i 1,2,...,(M 2), |
( 1)i ( ) B( ,a), |
||||
i |
i |
|
||
где — модуль максимальной ошибки аппроксимации; перепишем с учетом
(9.1):
|
M |
a |
|
|
M k , |
i 1,2,...,(M 2), |
( 1)i ( ) |
|
cos |
||||
i |
k |
|
i |
|
|
|
k 0
откуда имеем систему из (M 2) линейных алгебраических уравнений (СЛАУ):
M |
a |
|
|
|
M k |
|
i 1,2,...,(M 2) |
(9.8) |
|
k |
cos |
( 1)i ( ), |
|||||
|
|
i |
|
i |
|
|
||
k0
с(M 2) неизвестными ak и .
Для решения СЛАУ (9.8) используется численный метод, известный как обменный алгоритм Ремеза (в англоязычной литературе алгоритм Паркса—Мак- Клиллена).
Пример 9.2
Определить порядок КИХ-фильтра 1-го типа с АЧХ на рис. 9.2:
m 11
M m 2 9
R 2M 18
ФЧХ КИХ-фильтра — линейна с точностью до скачков на в точках, где АЧХ = 0.
4
A( ) |
|
|
1 |
|
|
0 |
|
|
|
|
|
|
k |
|
( ) |
|
|
Рис. 9.2. АЧХ и ФЧХ КИХ-фильтра ФНЧ 1-го типа |
||
9.3.Итерационная процедура синтеза оптимального КИХ-фильтра
1.Задание требований к АЧХ.
2.Оценка начальной длины КИХ-фильтра (по эмпирической формуле).
3.Синтез КИХ-фильра — расчет передаточной функции.
Для КИХ-фильтра это сводится к расчету ИХ h(n).
Вметоде чебышевской аппроксимации это сводится к расчету вектора коэффициентов тригонометрического полинома a .
4.Уточнение порядка КИХ-фильтра в результате проверки выполнения требований
кАЧХ:
если не выполняются — порядок увеличивается.
если выполняются — порядок уменьшается.
В результате определяют оптимальный порядок Ropt .
При увеличении/уменьшении порядка необходимо обращать внимание на тип избирательности и тип КИХ-фильтра!!!
5. Выбор структуры КИХ-фильтра — прямой или прямой приведенной.
