
лекции / DSP_7
.pdf
1
Лекция 7. Цифровые фильтры
1.Определение и классификация ЦФ.
2.Основные этапы проектирования ЦФ.
3.Задание требований к АЧХ.
4.КИХ-фильтры с линейной ФЧХ.
5.Четыре типа КИХ-фильтров с ЛФЧХ.
6.Прямая приведенная структура КИХ-фильтра.
7.1. Определение и классификация ЦФ
Цифровым фильтром (ЦФ) называют ЛДС, выполняющую преобразование входной последовательности в выходную по алгоритму, описываемому РУ, который отображается заданной структурой, реализованной программно или аппаратно.
В узком смысле под ЦФ подразумевают частотно-избирательные ЦФ, предназначенные для выделения спектральных составляющих, расположенных в ПП, и подавления спектральных составляющих, расположенных в ПЗ.
По типу избирательности различают: ФНЧ, ФВЧ, ПФ и РФ.
По типу ЛДС различают: КИХ и БИХ-фильтры.
7.2. Основные этапы проектирования ЦФ
Основные этапы проектирования ЦФ:
1.Задание требований к АЧХ.
2.Выбор типа ЦФ (КИХ или БИХ).
3.Выбор метода синтеза.
4.Синтез ЦФ — расчет передаточной функции H(z) .
5.Выбор структуры ЦФ.
6.Компьютерное моделирование структуры ЦФ с учетом конечной разрядности данных.
7.Реализация структуры ЦФ на ЦПОС, ПЛИС и т. п.
7.3.Задание требований к АЧХ
Требования задаются к нормированной АЧХ в основной полосе частот 0; fд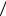 2 и
2 и
включают в себя (рис. 7.1—7.4):
□частоту дискретизации fд ;
□граничные частоты полос пропускания (ПП) и полос задерживания (ПЗ);
□максимально допустимые отклонения АЧХ.
Для БИХ-фильтров требования задаются к АЧХ в децибелах — к характеристике затухания:
a( f ) 20lg A( f ) (дБ) |
. |
(7.1) |
|
|
|
В требованиях к характеристике затухания вместо значений максимально допустимых отклонений 1, 2 задаются:
□amax (дБ) — максимально допустимое затухание в ПП;
□amin (дБ) — минимально допустимое затухание в ПЗ.
2
ξ(f ) |
|
|
1 |
|
|
0 |
|
f |
fχ |
|
fд /2 |
A(f) |
|
|
1 δ |
|
|
11 |
|
|
1 δ1 |
|
|
ПП |
|
ПЗ |
|
|
|
δ2 |
|
f |
0 |
fk |
|
fχ |
fд /2 |
a(f )
amin
amax |
|
|
|
|
|
|
0 |
|
|
|
|
|
f |
|
|
|
|
|
||
amax |
|
fχ |
fk |
fд 2 |
||
Рис. 7.1. ФНЧ: идеальная АЧХ; требования к АЧХ;
требования к характеристике затухания
ξ( f )
1 |
|
|
|
|
а |
|
|
|
|
|
|||
|
|
|
|
|
||
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
fχ |
fд |
|
|||
0 |
/2 |
|||||
A(f)
1 δ 1
1
1 δ1
ПЗ |
ПП |
б |
δ 2
0 |
|
|
|
f |
f k |
fχ |
|
||
|
f д / 2 |
|||
Рис. 7.2. ФВЧ: идеальная АЧХ; требования к АЧХ

3
ξ( f )
1 |
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
0 |
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
f χ |
fχ |
|
|
fд |
|
||||
A(f) |
|
|
/ 2 |
|||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 δ1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
б |
|
1 δ1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||||||
2 |
ПЗ1 |
|
ПП |
|
|
|
|
ПЗ2 |
||||
|
|
|
|
|
|
|
|
|
|
|
f |
|
0 |
|
|
|
|
|
fχ |
|
|
|
|
||
|
f k |
f χ |
fk fд / 2 |
|||||||||
Рис. 7.3. ПФ: идеальная АЧХ; требования к АЧХ
ξ( f )
1
|
|
|
|
|
|
|
а |
|
0 |
|
|
|
|
|
|
|
f |
|
|
f |
χ |
f |
χ |
fд / 2 |
||
A(f) |
|
|
|
|
|
|
||
1 δ1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 δ1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б
ПП1 ПЗ ПП2
δ2 |
|
|
|
|
|
|
|
|
f |
0 |
f χ |
f k |
fk fχ |
f |
|
||||
|
д / 2 |
||||||||
Рис. 7.4. РФ: идеальная АЧХ; требования к АЧХ
7.4. КИХ-фильтры с линейной ФЧХ
Условие линейности ФЧХ (ЛФЧХ): КИХ-фильтр с передаточной функцией:
N 1 N 1
H(z) biz i h(n)z n .
i 0 n 0
обладает строго линейной ФЧХ (с точностью до скачков на h(n) выполняется одно из двух условий:
симметрии:
(7.2)
π), если для его ИХ
h(n) h(N 1 n)
антисимметрии:
h(n) h(N 1 n).
Ось симметрии (антисимметрии) ИХ h(n) — в точке n N 1.
2
Скачок ЛФЧХ на π — в точках, где АЧХ равна нулю.
Длина КИХ-фильтра равна количеству коэффициентов передаточной функции N .
Порядок КИХ-фильтра равен порядку передаточной функции
R = N – 1.
7.5. Четыре типа КИХ-фильтров с ЛФЧХ
Различают 4 типа КИХ-фильтров с ЛФЧХ по следующим двум признакам:

4
четность/нечетность порядка;
симметрия/антисимметрия ИХ
Рассмотрим на примерах, результаты обобщим.
Для каждого типа КИХ-фильтра выполним следующие действия:
1.Изобразим ИХ — bi h(n), i n.
2.Запишем ПФ.
3.Определим возможные типы избирательности ЦФ. С этой целью определим значение АЧХ на границах основной полосы.
Пример 7.1 — 1-й тип КИХ-фильтра
Порядок — четный R = 4 (длина N = 5). ИХ h(n) — симметричная.
График ИХ
4
H(z) biz i b0 b1z 1 b2z 2 b1z 3 b0z 4 ;
i 0
A(0) H(z) z ej0 1 b0 b1 b2 b1 b0 0
A( ) H(z) z ej 1 b0 b1 b2 b1 b0 2b0 2b1 b2 0
Вывод: КИХ-фильтры 1-го типа могут использоваться для синтеза ЦФ любой избирательности.
Пример 7.2 — 2-й тип КИХ-фильтра
Порядок — нечетный R = 3 (длина N = 4). ИХ h(n) — симметричная.
График ИХ
3
H(z) biz i b0 b1z 1 b1z 2 b0z 3 ;
|
|
|
|
i 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
A(0) |
|
|
|
H(z) |
|
|
|
z ej0 1 |
|
|
b0 b1 b1 b0 |
|
|
|
2b0 2b1 |
|
0 |
||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
A( ) |
|
H(z) |
|
z ej 1 |
|
b0 b1 b1 b0 |
|
0 |
|
|
|||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Вывод: КИХ-фильтры 2-го типа могут использоваться для синтеза ФНЧ и ПФ.
Пример 7.3 — 3-й тип КИХ-фильтра
Порядок — четный R = 4 (длина N = 5). ИХ h(n) — антисимметричная.
График ИХ

5
4
H(z) biz i b0 b1z 1 0z 2 b1z 3 b0z 4 ;
i 0
A(0) H(z) z ej0 1 b0 b1 0 b1 b0 0
A( ) H(z) z ej 1 b0 b1 0 b1 b0 0
Вывод: КИХ-фильтры 3-го типа могут использоваться только для синтеза ПФ.
Пример 7.4 — 4-й тип КИХ-фильтра
Порядок — нечетный R = 3 (длина четная N = 4). ИХ h(n) — антисимметричная.
График ИХ
3
H(z) biz i b0 b1z 1 b1z 2 b0z 3 ;
i 0 |
|
|
A(0) H(z) z ej0 1 |
b0 b1 b1 b0 |
0 |
A( ) H(z) z ej 1 b0 b1 b1 b0 0
Вывод: КИХ-фильтры 4-го типа могут использоваться для синтеза ФВЧ и ПФ.
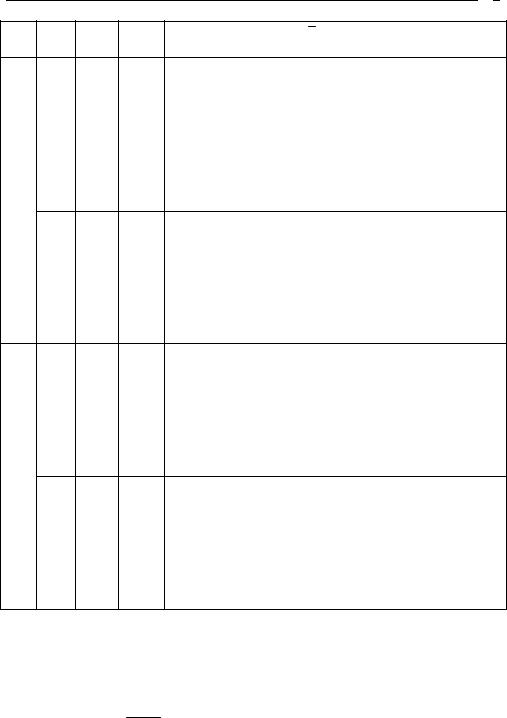
6
ИХ Тип h(n) КИХ
1
Симметричная
2
3
Антисимметричная
4
Пор-к Длина
R N
Четный |
Нечетная |
Нечетный |
Четная |
Четный |
Нечетная |
Нечетный |
Четная |
Амплитудная функция B( |
a |
, ) |
|
ФЧХ |
Тип |
|||||||||||||||||||||||
|
|
|
|
|
Порядок полинома M |
|
|
избир |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
B(a, ) ak cos M |
k |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ФНЧ |
||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h(M k), |
k M; |
|
|
|
|
|
|
|
ФВЧ |
||||||||||||||
|
|
|
|
|
|
|
|
|
R |
|
||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
ak |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
ПФ |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k M, |
|
|
2 |
|
|
||||||
|
|
|
|
|
h(k), |
|
|
|
|
|
|
|
|
|
|
|
РФ |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
M |
cos M |
|
|
|
|
|
|
|
|
|
|
|||||||||
B(a, ) ak |
k |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
1 |
h M k |
|
|
|
|
|
|
R |
|
ФНЧ |
||||||||||
|
|
|
|
|
|
ak |
|
|
|
|
|
|
|
ˆ |
|
|||||||||||||
|
|
|
|
|
|
2 |
|
|
2 |
ПФ |
||||||||||||||||||
|
|
|
|
|
|
|
M |
R 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
M |
sin M |
|
|
|
|
|
|
|
|
|
|
|||||||||
B(a, ) ak |
k |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
1 |
h M k |
|
|
|
|
|
|
R |
ˆ |
ПФ |
||||||||||
|
|
|
|
|
|
ak |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
2 |
2 |
||||||||||||||||
|
|
|
|
|
|
|
M |
R |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
sin M |
|
|
|
|
|
|
|
|
|
|
|||||||||
B(a, ) ak |
k |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
ak |
|
1 |
h M k |
|
|
|
|
|
|
R |
ˆ |
ПФ |
||||||||||
|
|
|
|
|
|
|
2 |
|
2 |
2 |
ФВЧ |
|||||||||||||||||
|
|
|
|
|
|
|
M |
R 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
7.6. Прямая приведенная структура КИХ-фильтра
Прямая приведенная структура используется для КИХ-фильтров с ЛФЧХ.
Пример 7.5
Изобразить прямую приведенную структуру КИХ-фильтра 1-го типа длины N 7.
Ось симметрии n N 1 3.
2
Передаточная функция с учетом симметрии ИХ:
H(z) b0 b1z 1 b2z 2 b3z 3 b2z 4 b1z 5 b0z 6 .
Приведение подобных слагаемых (отсюда название структуры — приведенная):
H(z) b0(1 z 6) b1(z 1 z 5) b2(z 2 z 4) b3z 3.
Разностное уравнение:
y(n) b0 x(n) x(n 6) b1 x(n 1) x(n 5) b2 x(n 2) x(n 4) b3x(n 3)
В прямой приведенной структуре сокращается вдвое число умножителей.
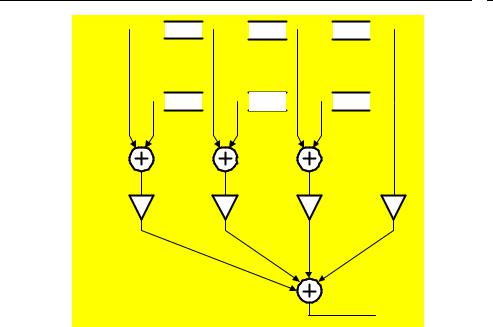
7
x(n) 
 z 1
z 1  z 1
z 1 

 z 1
z 1 
 z 1
z 1  zz 1
zz 1  z 1
z 1 

b0 |
b1 |
b2 |
b3 |
 y(n)
y(n)
Рис. 7.5. Приведенная структура КИХ-фильтра 1-го типа длины N = 7
